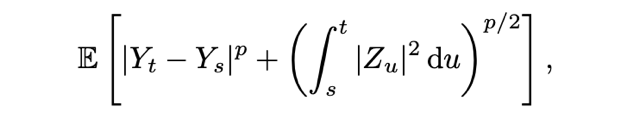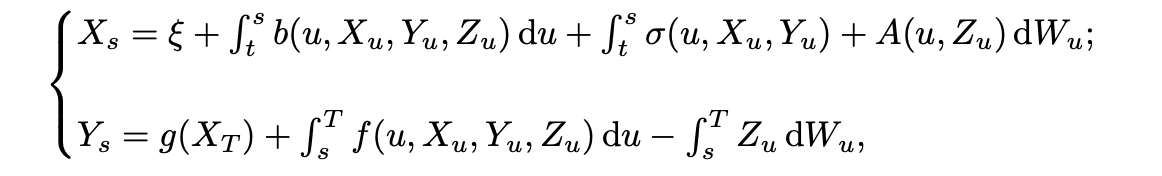Stochastic Sauna
Aalto University, December 19–20, 2024
Stochastic Sauna is a traditional workshop that brings together researchers and students working on probability, statistics, and their applications. The workshop will be held on Thu 19–Fri 20 December 2024.

Confirmed speakers
- Ariane Carrance (University of Vienna)
- Colin Desmarais (TU Wien)
- Mohamed Fkirine (Tampere University)
- Alex Karrila (Åbo Akademi University)
- Petri Laarne (University of Helsinki)
- Mikko Parviainen (University of Jyväskylä)
- István Prause (Åbo Akademi University)
- Lukas Schoug (University of Helsinki)
- Paul Thevenin (Angers University)
- Xilin Zhou (University of Jyväskylä)
Venue
All talks take place at Hall M1, Aalto University, Otakaari 1, Espoo, Finland. The lecture hall is equipped with a blackboard, beamer, and a computer.
Tentative Schedule
| |
|
|
| 11:50 |
Opening |
|
| 12:00–12:45 |
Laarne |
|
| 13:00–13:45 |
Parviainen |
|
| 13:45–14:15 |
Coffee |
|
| 14:15–15:00 |
Karrila |
|
| 15:00–19:00 |
Social program (Sauna @ Löyly, Hernesaarenranta 4, Helsinki) |
|
| 20:00- |
Dinner (self-organized @ Zetor, Mannerheimintie 3–5, Helsinki) |
|
| |
|
|
| Fri, Dec 20, 2024 |
|
|
| |
|
|
| 9:45–10:30 |
Thevenin |
|
| 10:45–11:30 |
Carrance |
|
| 11:30–13:00 |
Lunch (self-organized) |
|
| 13:00–13:45 |
Desmarais |
|
| 14:00–14:45 |
Prause |
|
| 14:45–15:15 |
Coffee |
|
| 15:15–16:00 |
Fkirine |
|
| 16:15–17:00 |
Zhou |
|
Social program
The social program includes sauna (@ Löyly, Hernesaarenranta 4, Helsinki). Sauna is free for participants. Sauna is mixed, but the changing rooms will be reserved for male and female participants. Please bring your bathing suit. We have reserved tables at Restaurant Zetor, Mannerheimintie 3–5, Helsinki for the social dinner.
Registration
There is no participation fee, but registration is mandatory. Please fill in the registration form.
Abstracts
Ariane Carrance (University of Vienna)
Limits of random trees with local catastrophes
In this talk, I will present a new model of random trees that naturally generalises Bienaymé-Galton-Watson (BGW) trees, in which deaths of individuals are now spatially correlated, through so-called "local catastrophes". In particular, contrary to BGW trees, this model no longer has the branching property. Despite this, we can show that, in the case where the probability distributions characterising the birth and death events have finite third moments, we recover the same scaling limit as for critical BGW trees with finite variance, that is, the Brownian forest.
This is based on joint work with J. Casse and N. Curien [arXiv 2401.06770].
Colin Desmarais (TU Wien)
A noisy K-branching random walk
We examine a population model that evolves according to the following procedure. At each step, each individual produces a large number of offspring that inherit the fitness of their parents up to independent and identically distributed fluctuations. The next generation consists of a random sampling of all the offspring so that the population size remains fixed, where the sampling is made according to a parameterized Gibbs measure of the fitness of the offspring. We show that as we increase the population size, the random dynamics of the model can be described by deterministic transformations of the limiting population densities under proper rescaling. We then show that for certain distributions of the fitness fluctuations, these transformations exhibit a travelling wave solutions, and we prove local stability of the travelling wave.
Based on ongoing work with Emmanuel Schertzer and Zsófia Talyigás.
Mohamed Fkirine (Tampere University)
On evolution equations with white-noise boundary conditions
In this talk, we delve into the study of evolution equations with white-noise boundary conditions. By rewriting these equations as stochastic Cauchy problems, we establish necessary and sufficient conditions for the existence of solutions. Additionally, we examine the robustness properties of these equations, including well-posedness, absolute continuity, and the existence of invariant measures under various types of unbounded perturbations.
This is joint work with S. Hadd and A. Rhandi.
Alex Karrila (Åbo Akademi University)
Uniform spanning trees, degenerate correlation functions of CFT, and fused SLEs
The uniform random spanning tree (UST) on a finite subgraph of the integer lattice Z^2 is an archetypal example of a critical discrete planar model, which are generally expected to exhibit conformal invariance in the scaling limit. Many such properties have also been proven over the past two decades, e.g., in terms of physics predictions from Conformal field theory (CFT), or purely mathematically in terms of conformally invariant random geometry.
In the present talk, we study connectivity events of multiple UST boundary branches, with potentially fused endpoints and in any topological connectivity. The scaling limits of their probabilities are found explicitly and shown to satisfy various properties of CFT (c=-2) degenerate correlation functions, in particular conformal covariance, fusion rules, and so-called BPZ PDEs. In CFT language, these limits are interpreted as covering the entire first row of the Kac table, hence providing arguably the widest rigorously known dictionary between a discrete model and a CFT. In the random geometry direction, we rigorously relate both the discrete model and the limiting probabilities to fused SLE (kappa=2) type random curves.
Based on an ongoing work with Augustin Lafay, Eveliina Peltola and Julien Roussillon.

Petri Laarne (University of Helsinki)
Metastable dynamics of the hyperbolic phi^4 model
We consider a stochastic wave equation with a symmetric double-well potential. The solutions spend long times near potential minima, but jump occasionally between them. What is the average frequency of jumping? I will sketch how this is answered with stochastic quantization. I will also briefly comment on the very different parabolic problem.
Based on recent preprint (arXiv:2410.03495) with Nikolay Barashkov.
Mikko Parviainen (University of Jyväskylä)
Regularity for a general class of discrete stochastic processes
In this talk, we consider an asymptotic regularity for expectations of a quite general class of discrete stochastic processes. Such expectations can also be described as solutions to a dynamic programming principles or as solutions to discretized PDEs. The result, which is also generalized to functions satisfying Pucci-type inequalities for discrete extremal operators, can be seen as a counterpart to the Krylov-Safonov regularity result in PDEs. However, the discrete step size has some crucial effects compared to the PDE setting. The proof combines analytic and probabilistic arguments. The result directly applies to a version of the tug-of-war with noise.
This talk is partly based on a joint work with Ángel Arroyo and Pablo Blanc.
István Prause (Åbo Akademi University)
The genus-zero five-vertex model
The five-vertex model is a probability measure on monotone nonintersecting lattice path configurations on the square lattice where each corner-turn is penalised by a fixed weight. I’ll introduce an inhomogeneous “genus-zero” version of this non-determinantal model and study its limit shape problem. That is, we are interested in the typical shape of configurations for large system size and fixed boundary conditions. We will emphasise new features in this setting going beyond determinantal models.
The talk is based on joint work with Rick Kenyon.
Paul Thevenin (Angers University)
Random meandric systems and the infinite noodle
A meandric system of size n is a configuration of noncrossing loops intersecting the horizontal axis at exactly 2n points. These objects were introduced in an attempt to answer a long-lasting question of Poincaré about topological configurations of two curves on the sphere. We prove that the number of connected components in a uniformly chosen random meandric system behaves linearly in n. The main ingredient of the proof is the convergence of this random meandric system towards an infinite discrete object called the infinite noodle. If time allows, I will present some interesting structural properties of the infinite noodle.
Xilin Zhou (University of Jyväskylä)
Decoupling of forward-backward stochastic differential equations on the Wiener space, and applications to regularity
For any $ p\geq 2$, S. Geiss and J. Ylinen [1] introduced the decoupling method to investigate the $L_p$ regularity in time of the solution to backward stochastic differential equations (BSDEs): specifically focusing on estimates for
where recently, using the chaos decomposition and decoupling method, S. Geiss and X. Zhou [2] provided a characterization of the Malliavin–Sobolev space $D_{1,2}$. It is shown that the aforementioned regularities are strongly connected to estimates involving a special structure derived using the decoupling method, referred to as the decoupling variance.
In this talk, we explore the decoupling method in the context of forward-backward stochastic differential equations (FBSDEs) of the form:
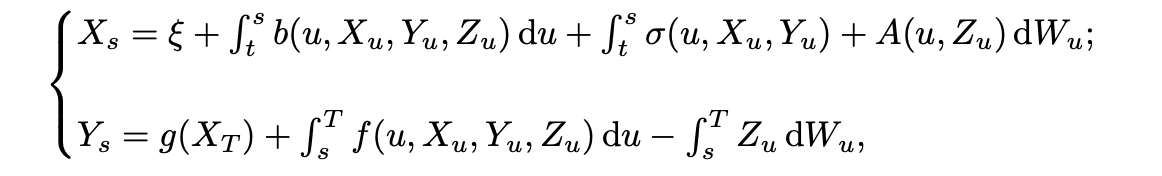
with all the random coefficients being uniformly Lipschitz in $(x,y,z)$, and $A$ further assumed to be linear in $z$.
We derive estimates for the $p$-decoupling variance when length of the time interval is sufficiently small. Furthermore, under the decoupling field structure studied in [3], these estimates are extended to arbitrary time intervals with finite length. As applications, we establish the regularity results for solutions to FBSDEs, including $L_p$ regularity in time and $D_{1,2}$ differentiability, in some special case.
[1] S. Geiss and J. Ylinen, Decoupling on Weiner Space, Related Besov Spaces, and Applications to BSDEs, Memoirs of AMS, 2021.
[2] S. Geiss and X. Zhou, Coupling of stochastic differential equations on the Wiener space, in preparation.
[3] Ma, Z. Wu, D. Zhang, J. Zhang, On well-posedness of forward-backward SDEs – A unified approach. Ann. Appl. Probab. 25(4):2168–2214.
Organizers
The workshop is hosted by the Department of Mathematics and Systems Analysis, Aalto University and organized by
Sponsors
Research Council of Finland (former Academy of Finland)
Finnish Centre of Excellence in Randomness and Structures (FiRSt)
Matematiikan Rahasto, Finnish Academy of Science and Letters
Department of Mathematics and Systems Analysis, School of Science, Aalto University





Page content by: webmaster-math [at] list [dot] aalto [dot] fi