Osa 2. Matriisityöskentelyä |
Otamme esille kestävän kehityksen periaatteet, jotka toimivat luotettavasti kaikissa ympäristöissä ja versioissa. (Tulevaisuudesta emme voi mennä takuuseen, versio 6 edustaa nykyhetkeä.)
>> diary doku % Avataan tiedosto doku >> A=eye(10) % Matlab-komennot ja tulosteet kirjoittuvat >> mesh(A) % doku-tiedostoon >> diary % Suljetaan tiedosto >> type doku % Katsotaan, tuliko mitäänJos halutaan antaa nimeksi vaikkapa doku.txt , on komennettava >> diary 'doku.txt', type 'doku.txt'
Editoidaan doku.txt-tiedostosta turhat tulosteet, virheilmoitukset ym. pois ja lisätään kommentteja, selostusta ym.
Kaikki ovat ihan käyttökelpoisia työtapoja. Viimemainittussa tulee muistaa antaa diary-komento ajoissa. Tosin Matlab-ikkunaa voi vierittää taaksepäin ja komentoja selata nuoli ylös-näpäimella, joten armonaikaa jää jonkinverran.
Varoitus: Älä luota save-komentoon
Monissa Matlab-oppaissa mainostetaan save-komentoa. Siitä ei ole dokumentin tallettamisen kannalta mitään hyötyä. Se mahdollistaa muuttujien tallettamisen levylle, mistä harvoin on hyötyä, paitsi jatketteassa laskentaa jollain muulla ohjelmalla. Tärkeämpää on yleensä tallettaa komennot, joilla muuttujat luotiin.
Tämä ei tarkoita, että komennot save ja load olisivat tekijän mielestä hyödyttömiä. Päinvastoin, datan siirtäminen eri ohjelmien välillä saattaa olla monessa tilanteessa todella välttämätöntä.
Komennot save ja load
Pelkkä save tallettaa kaikki muuttujat tiedostoon matlab.mat, josta ne saadaan palautetuksi komennolla load.
>> save 'tiedosto.txt' x y z -ascii tallettaa muuttujat x,y,z
mainittuun tiedostoon ascii-tekstinä.
Vastaavasti load 'tiedosto.txt' lataa ne työtilaan levyltä.
Kts. vanhaa L1.html ***
>> addpath /p/edu/mat-1.414/matlab/ >> addpath /p/edu/mat-1.414/matlab/laode/Nämä ovat tarpeen V-peruskursseilla, tällöin Matlab-kurssihakemistoon sijoitetut m-tiedostot ovat suoraan käytettävissä.
Jotta näitä ei aina tarvitse toistaa kannattaa kirjoittaa ne oman kotihakemiston alla olevaan matlab-hakemiston tiedostoon
startup.m
Tämä tapahtuu Unix-komennoilla
(Ollaan käyttöjärjestelmäikkunassa.) > cd % Kotihakemistoon > mkdir matlab % Luodaan matlab-hakemisto (ellei ole jo) > emacs matlab/startup.m & %Kirjoitetaan editoriin ainakin rivit (jos ollaan V3-kurssilla): addpath /p/edu/mat-1.414/matlab/ addpath /p/edu/mat-1.414/matlab/laode/Tehtävä: Tee tämä ja heti!
Kertolasku (*) on nimenomaan matriisikertolasku. Jos halutaan laskea kahden samankokoisen matriisin (vektorin) tulo vastinalkioittain (pisteittäin), kirjoitetaan kertomerkin eteen pite (.).
Jakolasku A\B tai A/B tarkoittaa matriisioperaationa yhtälöryhmän ratkaisemista ja taulukko-operaationa (A./B) yksinkertaisesti vastinalkioittain tapahtuvaa jakoa. (Taulukkotapauksessa A.\B on sama kuin A./B) .
Potenssiin korotus A^p tarkoittaa matriisioperaationa tuloa A*A*...*A ja edellyttää siten, että A on neliömatriisi. Taulukko-operaatio A.^B tarkoittaa vastinalkioittain muodostettuja potensseja ja edellyttää samankokoisia matriiseja (joista toinen voi olla skalaari). Kokoamme taulukkoon:
Matlabin laskutoimitukset
|
Oikeanpuoleiset taulukko-operaatiot suoritetaan siis aina vastinalkioittain ja ne edellyttävät, että operandimatriisit ovat samankokoiset. Jos toinen operandi on skalaari (1 x 1 - matriisi), niin tätä samaa skalaaria käytetään operandina jokaisessa laskutoimituksessa. (Taulukko-operaatioiden kohdalla voidaan ajatella, että Matlab laajentaa skalaarin samankokoiseksi vakiomatriisiksi toisen operandin kanssa.)
Vasemman sarakkeen matriisioperaatiot edellyttävät, että operandit ovat oikean kokoisia kyseiseen toimitukseen. Tässäkin tapauksessa skalaarilla operoiminen onnistuu aina. On syytä huomata, että potenssiin korotuksessa ja jakolaskussa matriisi- ja taulukko-operaatiot eivät ole samoja, vaikka toinen argumentti olisi skalaari. Kertolaskussa sensijaan skalaarin ja matriisin tulo on sama kuin pisteittäinen tulo.
>> x=A\bsaamme lineaarisen yhtälösysteemin A*x = b ratkaisuvektorin x . Kyseessä on neliömatriisin A tapauksessa sama asia kuin laskussa
>> x=inv(A)*bTosin käänteismatriisilla kertominen on numeerisen laskennan tehokkuuden ja tarkkuuden kannalta epäedullisempaa.
Tässä b:n on oltava A:n sarakkeen pituinen sarakevektori tai matriisi, jossa tällaisia sarakevektoreita on ladottuna vierekkäin.
Muistisäänöt:
Mainittakoon vielä, että matriisijakolaskussa A:n ei tarvitse olla neliömatriisi. Ellei se ole, ratkaisu suoritetaan PNS-mielessä. (Palataan lähemmin.)
Toisin kuin Maplessa, Matlabissa ei voida käsitellä "vapaita" muuttujia.Jos käytetään lisäpakkausta "symbolic toolbox", voidaan suorittaa myös symbolisia operaatioita, mutta tässä käsittelemme vain Matlabin perusajatusmaailmaa.
>> x=[-2,-1,0,3,5]
>> x2=x.^2 % x-vektorin 2. potenssit.
>> x^2 % Matriisipotenssi on tuomittu epäonnistumaan.
>> x.*exp(x) % exp toimii "pisteittäin", kerrotaan exp-arvot
% pisteittäin x-arvoilla.
>> x=linspace(-1,2); % 100-pituinen diskretoitu x-akselin pätkä.
>> plot(x,x.*exp(x)) % Yhdistetään kuvaajan 100-pistettä pikku janoilla.
Tee itsellesi selväksi pisteittäiset, vastinalkioittain toimivat operaatiot.
Matriisilausekkeita , vaikkapa matriisipolynomeja voidaan muodostaa, kunhan matriisit ovat kertomiskelpoisia, polynomin tapauksessa samankokoisia neliömatriiseja. Laskutoimitukset ovat silloin normaaleja, keskimmäisen sarakkeen pisteettömiä operaattorisymboleja, emmekä niitä siksi tässä yleisesittelyssä ryhdy esimerkein valaisemaan.
| Matlab | Maple |
|---|---|
| >> muuttuja=lauseke Loppumerkki ei pakollinen (;) estää tulostuksen |
> muuttuja:=lauseke;
Loppumerkki (; tai :) pakollinen, kaksoispiste estää tulostuksen. |
Muuttujan nimissä erotellaan pienet ja isot kirjaimet, siten esimerkiksi x ja X edustavat eri muuttujaa. Tämä pätee niin Maplen kuin Matlabin suhteen. Tuttu englanninkielinen termi "case sensitive" pätee siten molempiin.
Kuten todettu, Matlabissa ei ole vapaita muuttujia, kuten Maplessa. Tämä yksinkertaistaa evaluointimekanismia merkittävästi. Jos evaluonnissa törmätään muuttujaan, jolla ei ole arvoa, saadaan virheilmoitus. (Maplen evaluointisääntöjä on käsitelty mm. viitteessä [HAM].)
Matemaattisten lausekkeiden käsittely on siten Maplessa mukavampaa ja luontevampaa (myös vapaiden muuttujien takia).
Toisaalta Maplessa on tiettyjä komplikaatioita matriisien käsittelyssä. Asia
on paranemaan päin versiossa Maple 6 kehitetyn LinearAlgebra- pakkauksen
ansiosta. Kuitenkin siirtymäkauden hankaluuksia esiintyy, koska nykyisellään on
myös tarvetta vanhempaan linalg-syntaksiin.
Matlab on numeeristen
matriisien käsittelyssä ylivertaisen yksinkertainen ja lisäksi tehokas Mapleen
verrattuna. (Symbolisia matriiseja ei Matlabilla tietenkään voi käsitellä.)
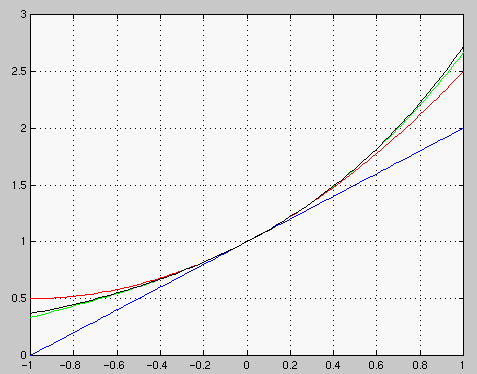
Esimerkki "algebrallisesta" lausekkeesta
x=linspace(-1,1); y1=1+x; y2=y1+(x.^2)/2; y3=y2+(x.^3)/(1*2*3); plot(x,y1,'b',x,y2,'r',x,y3,'g',x,exp(x),'k') >> plot(x,y1,'b',x,y2,'r',x,y3,'g',x,exp(x),'k') >> shg >> grid |

Tehtävä. Suorita Matlabissa yllä olevat komennot. Piirrä samaan kuvaan vielä astetta 5 oleva Taylorin polynomi jollain edellisistä erottuvalla värillä. Voit joko editoida komentoikkunassa yllä olevaa plot-komentoa tai lisätä yksittäisen kuvaajan komentamalla ennen piirtämistä hold on .
Esimerkki matriisilausekkeesta
>> rand('state',0)
>> A=rand(2,2);
>> S1=eye(2,2)+A;
>> S2=S1+(A^2)/2;
>> S3=S2+(A^3)/(1*2*3);
>> S4=S3+(A^4)/(1*2*3*4);
>> [A,S1,S2,S3,S4,expm(A)]
ans =
Columns 1 through 7
0.9501 0.6068 1.9501 0.6068 2.4716 1.0426 2.6704
0.2311 0.4860 0.2311 1.4860 0.3971 1.6742 0.4642
Columns 8 through 12
1.2187 2.7278 1.2702 2.7441 1.2849
1.7383 0.4838 1.7562 0.4894 1.7613
|
Tulosta on syytä katsoa ajattelemalla sitä vierekkäisinä 2 x 2-matriiseina. Kirjoitetaan yleisemmin for-silmukalla, käytetään samalla uudempaa Matlabin tietorakennetta, solumatriisia, jossa kukin 2 x 2 - matriisi on alkiona "matriisivektorissa" P. (Solumatriisin käyttö ei olisi mitenkään välttämätöntä, sen hyöty tässä yhteydessä on lyhentää laskentakaavaa jakamalla toiminta kahteen for-silmukkaan. Saammepa samalla ensituntuman uuteen tietorakenteeseen (versiossa 5 tulleeseen).
>> for k=1:20; P{k}=(A^k)/prod(1:k); end % Tässä on kätevää käyttää
% solumatriisia P ("cell array")
>> S=eye(2,2);for k=1:20; S=S+P{k}; end
>> [S,expm(A)]
ans =
2.7441 1.2849 2.7441 1.2849
0.4894 1.7613 0.4894 1.7613
>> format long % Täysi tulostustarkkuus
>> [S,expm(A)]
ans =
2.74410134440431 1.28494639715736 2.74410134440431 1.28494639715736
0.48941951062196 1.76130317613298 0.48941951062196 1.76130317613298
>> format short % Palataan alkuperäiseen tulostustarkkuuteen.
|
Huomaa ero x.^k, A^k. Lukija, joka tuntee matriisieksponenttifunktion, huomaa heti mistä on kyse. Sellaiselle lukijalle, joka ei ole tätä käsitettä kohdannut, esimerkki voi avata uusia huikeita näköaloja (?!)
a:b % vektori: [a,a+1,...,b] a:h:b % vektori: [a,a+h,...,b]Viimeinen alkio voi jäädä b:tä vähän pienemmäksi, jos jako "ei mene tasan", mutta se on harvemmin tärkeää. Kts. myös help colon .
Esim:
>> -5:6
ans =
-5 -4 -3 -2 -1 0 1 2 3 4 5 6
>> -3.1:0.1:-2
ans =
Columns 1 through 7
-3.1000 -3.0000 -2.9000 -2.8000 -2.7000 -2.6000 -2.5000
Columns 8 through 12
-2.4000 -2.3000 -2.2000 -2.1000 -2.0000
>> 2:-0.5:-1
ans =
2.0000 1.5000 1.0000 0.5000 0 -0.5000 -1.0000
|
Viimeinen esimerkki havainnollistaa sitä, että pienenevän jonon saamme kätevästi ottamalla negatiivisen askelpituuden h.
Usein on tarpeen jakaa annettu väli tasan n:ään osaan. Se voitaisiin tehdä tyyliin
h=(b-a)/n x=a:h:bTähän on myös valmis funktio linspace , vanha tuttavamme.
> x=linspace(a,b,n);
Funktiolla linspace on myös muoto linspace(a,b), jolloin n:n oletusarvona käytetään lukua 100. Tämä on tavallisessa käyrien piirtämisessä usein sopiva arvo.
> a:=-Pi: b:=Pi: n:=20:
> h:=(b-a)/n;
h := 1/10 Pi
> x:=seq(a+k*h,k=0..n);
x := -Pi, - 9/10 Pi, - 4/5 Pi, - 7/10 Pi, - 3/5 Pi, - 1/2 Pi, - 2/5 Pi,
- 3/10 Pi, - 1/5 Pi, - 1/10 Pi, 0, 1/10 Pi, 1/5 Pi, 3/10 Pi, 2/5 Pi,
1/2 Pi, 3/5 Pi, 7/10 Pi, 4/5 Pi, 9/10 Pi, Pi
|
Esim:
>> v=rand(1,7)
v =
0.7382 0.1763 0.4057 0.9355 0.9169 0.4103 0.8936
>> v(2:5)
ans =
0.1763 0.4057 0.9355 0.9169
|
Mikään ei estä ottamasta mitä tahanasa jonoa vektorin indekseiksi kelpaavia kokonaislukuja (siis välillä 1 ... length(v)). Samaa lukua saa toistaa ja indeksilukujen järjestys saa hypähdellä miten vain.
>> v([1 1 1 2 7 6 6 3])
ans =
Columns 1 through 7
0.7382 0.7382 0.7382 0.1763 0.8936 0.4103 0.4103
Column 8
0.4057
|
Vektorin osalle voidaan sijoittaa arvoksi jokin toinen vektori yksinkertaisesti tyyliin
>> v(1:4)=[2 4 6 8]
v =
2.0000 4.0000 6.0000 8.0000 0.9169 0.4103 0.8936
Tehtävä Miten kääntäisit vektorin alkiot vastakkaiseen järjestykseen
kaksoispistettä käyttäen?
>> A=[1 2 3;4 6 5]Matlabissa on koko joukko tehokkaita funktioita erilaisten matriisien muodostamiseen. Eri tavoin muodostetuista osamatriiseista voidaan rakentaa isompia matriiseja näitä periaatteita noudattaen:
>> A=[1 2 1;-1 2 3;-10 -11 -12]
A =
1 2 1
-1 2 3
-10 -11 -12
>> b=[1;1;1]; % tai b=ones(3,1)
>> Ab=[A,b]
Ab =
1 2 1 1
-1 2 3 1
-10 -11 -12 1
>> A_alle_trb=[A;b']
A_alle_trb =
1 2 1
-1 2 3
-10 -11 -12
1 1 1
>> [A,A,A]
ans =
1 2 1 1 2 1 1 2 1
-1 2 3 -1 2 3 -1 2 3
-10 -11 -12 -10 -11 -12 -10 -11 -12
|
Otetaan tässä vertailu Mapleen.
Nämä ja monet muut tuottavat neliömatriisin, jos niitä kutsutaan vain yhdellä argumentilla. Tämä on joskus epäjohdonmukaista, siksi suosittelemme aina kahden argumentin käyttöä.
Esimerkki
>> [zeros(2,3),eye(2,2),ones(2,4)]
ans =
0 0 0 1 0 1 1 1 1
0 0 0 0 1 1 1 1 1
>> eye(size([ans;ans]))
ans =
1 0 0 0 0 0 0 0 0
0 1 0 0 0 0 0 0 0
0 0 1 0 0 0 0 0 0
0 0 0 1 0 0 0 0 0
|
| Eräitä matriisinmuodostamisfunktioita |
|---|
ones Ykkösistä koostuva matriisi
zeros Nollamatriisi
rand Satunnaislukumatriisi
diag Vektorista diagonaalimatriisi,
matriisin diagonaalivektori
spdiags Harvan matriisin muodostaminen diagonaaleista.
blkdiag Lohkodiagonaalimatriisi
repmat Matriisin rakentaminen toistamalla lohkoa.
|
Esimerkki
>> A=rand(3,4)
A =
0.4451 0.4186 0.2026 0.0196
0.9318 0.8462 0.6721 0.6813
0.4660 0.5252 0.8381 0.3795
>> diag(A)
ans =
0.4451
0.8462
0.8381
>> diag(diag(A))
ans =
0.4451 0 0
0 0.8462 0
0 0 0.8381
>> repmat(eye(2,2),2,3)
ans =
1 0 1 0 1 0
0 1 0 1 0 1
1 0 1 0 1 0
0 1 0 1 0 1
>> blkdiag(diag([-1,1]),2*ones(2,2))
ans =
-1 0 0 0
0 1 0 0
0 0 2 2
0 0 2 2
|
>> [diag([-1,1]),zeros(2,2);zeros(2,2),2*ones(2,2)]
Alkuunpääsyosasssa esittelimme lyhyesti matriisin osiin viittausta. Kerrataan vielä:
A(:,[2,4,7]) A:n sarakkeet 2,4,7 kokonaisuudessaan. A(2:4,[2,4,7]) Samoista sarakkeista rivit 2,3,4. A(:) A:n kaikki alkiot jonoutettuina sarakkeittain.Aivan kuten vektorien tapauksessa, voidaan matriisin osaa muuttaa suoralla sijoituksella vastaavaan osamatriisiin tähän tapaan:
>> A(1:2,[1 3 5])=-ones(2,3)
A =
-1 4 -1 10 -1
-1 5 -1 11 -1
3 6 9 12 15
>> A(1:2,[1 3 5])=-1
A =
-1 4 -1 10 -1
-1 5 -1 11 -1
3 6 9 12 15
Jälkimmäinen komento havainnollistaa, että jos korvaavan matriisin
alkiot ovat samoja, riittää antaa tuo yhteinen skalaari sijoituslauseessa.
(Tämä on tavallaan "skalaarin laajennussäännön ilmentymä".)