Osa 1. Alkuunpääsy

0. Johdanto

Cleve Moler kirjoitti alkuperäisen Matlabin Fortran-version 1970-luvun loppupuolella pienimuotoiseksi matriisilaskennan opetusohjelmaksi. Kyseessä oli Fortranilla kirjoitettu matriisitulkki, joka käytti LINPACK- ja EISPACK- kirjastojen rutiineja laskentakoneenaan. Vaiheita:

• 1978 "Klassinen" Matlab, alkuperäinen FORTRAN-versio
• 1984 Matlab 1, uudelleen kirjoitettu C-kielellä
• 1985 Matlab 2
• 1987 Matlab 3
• 1992 Matlab 4
• 1997 Matlab 5
• 2000 Matlab 6

Esikuvia kielelle: "Speak Easy" ja APL (Kenneth Iverson 1960-luvulla, Jim Brown, IBM Yorktown Heights: APL2 1984, ...)

Nykyisin : "Teollisuusstandardin asemassa", suuri määrä ammattimaisia toolboxeja.

Matlab on saatavissa kaikkiin ajateltavissa oleviin käyttöjärjestelmiin. Matlab-koodit ja työtilat talletetaan tekstimuodossa, mikä takaa ongelmattoman siirrettävyyden eri ympäristöjen välillä.

Matlab-ohjelman lisenssin omistaa The MathWorks, Inc.,

1. Käynnistys ja työtila, avustus

        use matlab
        matlab

        >> quit

                              < M A T L A B >
                  Copyright 1984-1999 The MathWorks, Inc.
                         Version 5.3.0.10183 (R11)
                                Jan 21 1999

 
  To get started, type one of these: helpwin, helpdesk, or demo.
  For product information, type tour or visit www.mathworks.com.

     matlab -nodesktop

Ohjelman käynnistyttyä, tulkki antaa kehotteen >> . Tällöin sille voidaan kirjoittaa Matlab-komentoja.

Mitä opimme:

• Matlab laskee liukuluvuilla, jotka saavat olla kompleksisia
• Perustietorakenne on matriisi (erikoistapauksena vektori).
• Matriisin rivit erotellaan puolipisteellä.

• Komennon loppumerkiksi riittää ENTER. Jos tulostus halutaan estää, lopetetaan puolipisteeseen (;)
• Matlab on "herkistynyt kirjainkoolle" ("case sensitive").
• Muuttujan sisältö nähdään kirjoittamalla sen nimi (ja pelkkä ENTER ).

Pienimuotoista Matlab-laskentaa voi harrastaa komentoikkunassa. Komentoja voi selata nuoli-ylös-näppäimellä samaan tapaan kuin Unix:n tcshellissä ja komentoriviä voi editoida.

Vähänkin vakavampihenkinen työskentely kannattaa järjestää erillistä editori-ikkunaa hyödyntäen. Editorina voi käyttää Matlabin omaa File-valikosta avautuvaa editoria (Windows:ssa jo versiossa 5, Unix:ssa versiosta 6 alkaen). Yhtä hyvin voi käyttää mitä tahansa tekstieditoria, Unix:ssa luonnollisin lienee Gnu Emacs .

Komennot voidaan kirjoittaa tekstitiedostoon, vaikkapa komennot.m. Kun tiedoston nimi (ilman m-tarkennetta) kirjoitetaan Matlab- komentoikkunassa, tulkki suorittaa komennot, aivan kuin ne kirjoitettaisiin peräkkäin Matlab-istuntoon. Siis >> komennot (tällöin on vain huolehdittava siitä, että tiedosto on joko työhakemistossa tai Matlab-polun (path) varrella. Vaihtoehtoisesti komennot voidaan koota tekstitiedostoon doku.txt tai vaikkapa doku.html. Tällöin tiedostossa olevia komentoja voidaan leikkaus/liimaus-hiirioperaatiolla siirtää komentoikkunan ja dokumentin välillä.

Komentojonotiedostoja kutsutaan lyhyesti skripteiksi. Skriptit ja funktiotiedostot ovat yhteiseltä nimeltään m-tiedostoja, molemmat ovat tyyppiä tied.m olevia tekstitiedostoja. Funktiotiedosto alkaa avainsanalla function ja se toimii, kuten funktion kuuluu: sille annetaan syöteparametreja, ja se palauttaa yhden tai useamman tulosarvon.

Katso lähemmin ja ... ref**

Avustus- ja opastus

     help, helpwin, helpdesk, lookfor

helpdesk käynnistää www-pohjaisen laajan avustus- ja opiskelujärjestelmän hakuineen ym.

• help - Matlab-hakemistorakenne (päähakusanat)
  • help aihe - aiheeseen aihe liittyvää apua
  • help help
  • help general - hakemiston general funktiot
  • help elfun - alkeisfunktiot
  • help specfun - erikoisfunktiot (myös lukuteoriaa ym.)
• doc - laaja www-pohjainen opasmateriaali.
  • Getting started -> The Matlab environment
• lookfor
  • lookfor elliptic, hyperbolic

Työtila

who   - muuttujien nimet
whos  - lisäksi koko- ja talletusinformaatio
clear - työtilan muuttujien vapauttaminen arvoistaan
why   - elämää suuremmat kysymykset

2. Vektorit ja matriisit

Vektoreita ja skalaareja voidaan pitää erikoistapauksina matriisista, viimemainittu on 1 x 1 - matriisi. Tästä ajattelusta seuraa, että rivivektorit ja sarakevektorit erotellaan toisistaan, edelliset ovat 1 x n - ja jälkimmäiset n x 1 - kokoisia matriiseja, missä n on vektorin pituus.

Versiosta 5 alkaen Matlabissa on myös sisäkkäisiä ja moniulotteisia rakenteita.

2.1 Matriisien muodostaminen ja alkioiden poiminta

Matriiseja voidaan luoda eri tavoilla:

• Kirjoittamalla alkioittain suoraan komentoikkunaan tai m-tiedostoon, joka suoritetaan kirjoittamalla sen nimi.
• Valmiilla matriisinluontifunktioilla.
• Lataamalla ulkoisesta tiedostosta komenolla load.

      >> A = [1 2 3; 4 5 6; 7 8 9]

Rivien erottimena on puolipiste, rivin alkioiden erottimena voidaan käyttää tyhjän ohella myös pilkkua. Rivierottimena käy myös rivinvaihto, selkeämpää lienee tällöin kirjoittaa myös puolipiste.
Sama matriisi voitaisiin siten kirjoittaa vaikkapa näin:

      >> A = [1 2 3; 
              4 5 6;
              7 8 9];

>> format compact  % Tulostusasua säätelevä komento.
>> v=[1 2 3 4 5]   % v=[1,2,3,4,5]  % Pilkut käyvät myös. 
v =
     1     2     3     4     5

>> v=1:5;             % Sama vektori saadaan kätevämmin näin.
                      % help colon (lähemmin kohdassa 11)
>> vt=v'              % Transponoidaan pystyvektoriksi.
vt =
     1
     2
     3
     4
     5
>> [1;2;3;4;5]        % Pystyvektori voidaan luoda myös suoraan.
ans =                 % Tässä emme sijoita sitä arvoksi millekään
     1                % muuttujalle. Matlab antaa sille nimen ans,
     2                % johon voidaan viitata, kuten mihin tahansa
     3                % muuttujaan. Tämä pätee vain viimeksi suoritettuun
     4                % komentoon. (Vrt. Maplen %)
     5 

Matriisin alkion poiminta

Vektorin (niin vaaka- kuin pysty) indeksointiin riittää yksi indeksi.

A(1,:) ilmaisee A-matriisin ensimmäisen rivin, yksinäinen kaksoispiste jälkimmäisenä indeksinä tarkoittaa, että sarakeindeksi käy läpi kaikki arvonsa . Vastaavasti A(:,2) tarkoitta A:n toista saraketta. Edelleen, A(2:4,3:6) poimii riveistä [2,3,4] sarakkeet [3,4,5,6]

Pelkkä kaksoispiste matriisin indeksinä tarkoittaa, että molemmat indeksit saavat kaikki mahdollset arvonsa. Tällöin tulee tietää, kumpaa matriisin indeksisuuntaa pidetään ensisijaisena. Paljastamme asian nyt: Matlab on sarakeorientoitunut, eli järjestys on : 1. sarake, 2. sarake, ...

Esim

>> A=reshape(1:12,4,3)   % Kätevä tapa muotoilla vektorista matriisi. 
>> A(:)                  % Jonoutus sarakkeittain.

Indeksointia ja kaksoispistenotaatiota käsitellään tarkemmin kohdassa 11 ... Kts. myös [SKK] 2.9, ss. 23 - 25.

2.2 Vektorilausekkeita, kuvaajan piirto

Halutkaamme piirtää funktio f(x)=sin(2*pi*x) välillä [0,1].
Tarvitsemme

• vektorin x=[x₁,x₂, ... ,x_n], missä 0 = x₁ < x₂ < ... < x_n = 1,
• vektorin y=[y₁,y₂, ... ,y_n], missä y_k= f(x_k), k=1 ... n ,
• murtoviivan, joka yhdistää koordinaattipisteet (x₁,y₁), ... , (x_n,y_n).

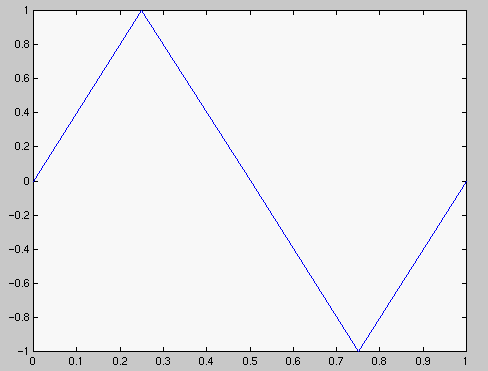
>> x=[0 0.25 0.5 0.75 1] % Havainnollisuuden vuoksi harva pisteistö. x = 0 0.2500 0.5000 0.7500 1.0000 >> y=sin(2*pi*x) % sin-funktio operoi jokaiseen x-vektorin % komponenttiin (skaalarifunktio) y = 0 1.0000 0.0000 -1.0000 -0.0000 >> [x' y'] % Pisteparien taulukko saadaan laittamalla pystyyn % transponoidut vektorit vierekkäin 2-sarakkeiseksi % matriisiksi.(Tämä vain asian havainnollistamiseksi) ans = 0 0 0.2500 1.0000 0.5000 0.0000 0.7500 -1.0000 1.0000 -0.0000 >> plot(x,y) % Yhdistetään edellä olevat (x,y)-parit murtoviivalla.

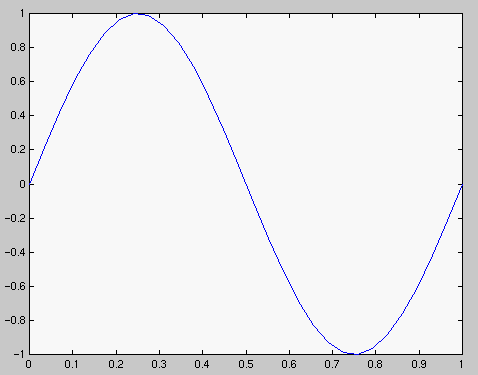
Jako 4:ään osaväliin	Jako 29:ään osaväliin

Tarkemman kuvan saamme jakamalla välin hienommin. Tähän on kaksi oivallista tapaa, joko muoto x=0:0.1:1; tai x=linspace(0,1,30); Kokeile tai lue lisää (tai help colon, help linspace) (Kaksoispiste on englanniksi "colon".) Homma hoituu näin:

>> x=linspace(0,1,30); y=sin(2*pi*x); plot(x,y)

  >> x=linspace(-pi/2,pi/2); 
  >> y=x.^2;            % Kukin vektorin komponentti toiseen potenssiin
  >> z=x.*sin(x);       % Vektorit x ja sin(x) kerrotaan "pisteittän"
  >> plot(x,y,x,z)

Varoitus! Aloittelevan Matlab-urheilijan tyypillinen virheloukku on pisteen unohtaminen "pisteittäisistä" vektorilaskutoimituksista.

2.3 Matriisiesimerkki, lineaarinen yhtälösysteemi

>> A=vander([1 2 3])   % Vandermonden matriisi on ei-singulaarinen,
                       % Matlabissa on valmis funktio sen muodostamiseen.
>> B=inv(A)
>> A*B                 % Katsotaan, onko B tosiaan käänteismatriisi.
>> A*B-eye(size(A))    % Yleisemmin voidaan samuutta testata näin.
>> b=[1;1;1]           % Haluamme ratkaista systeemin A*x = b .
>> x=B*b               % Kerrotaan käänteismatriisilla.
>> x=A\b               % Tehokkaampi tapa on käyttää \-operaatiota.
                       % Muistisääntö: "matriisijako, jossa jakajamatriisi 
                       % on jakoviivan alla.                      

Matriisijakolaskuun saat lisävalaistusta komentamalla help slash , kts. myös ...

2.4. Esimerkkejä Matlabin funktiosta

Komento help elfun antaa alkeisfunktioluettelon ("elementary functios").

Edellä olemme jo käytelleet joitakin funktioita. Otetaan pieni kommentein varustettu esimerkki-istunto, jossa esiintyy myös vanha tuttavamme linspace

Esim.

  
  >> x=linspace(0,5,10)
x =
  Columns 1 through 7 
         0    0.5556    1.1111    1.6667    2.2222    2.7778    3.3333
  Columns 8 through 10 
    3.8889    4.4444    5.0000
>> y=log(x)             % log on luonnollinen logaritmi 
Warning: Log of zero.
y =
  Columns 1 through 7 
      -Inf   -0.5878    0.1054    0.5108    0.7985    1.0217    1.2040
  Columns 8 through 10 
    1.3581    1.4917    1.6094

• Funktio linspace on kaikkein eniten tarvittavia datavektorin muodostamisfunktioita kaksoispistenotaation ohella. Tässä tapauksessa väli [0,5] jaetaan tasavälisiin osiin siten, että jakopisteiden lukumäärä on 10.

• Funktio log laskee (luonnollisen) logaritmifunktion arvon jokaisessa x-vektorin komponentissa ( skalaarifunktio).

• Vektorimme alkaa alkiosta 0. Laskenta ei kaadu tähän, vaan Matlab varoittaa asiasta ja sijoittaa y-vektorin 1. komponentiksi arvon -Inf (IEEE- aritmetiikkastandardin mukaisesti).

2.5. Tehtäviä

Piirrä log-funktion kuvaaja välillä (0,5) alkamalla yllä olevasta karkeasta diskretoinnista ja hienontaen sitten vaikkapa jakovölien lukumääriin 20,50,100.

Tehtävä 2

Fahrenheit-asteet saadaan Celsius-asteilla kaavasta F=1.8 C + 32 . Tee (käden käänteessä) 2-sarakkeinen taulukko, jossa on 5:n (C-) asteen välein arvot -40 ... 40 (siis C-sarake ja F-sarake vierekkäin).

Käännä taulukko myös vaakasuoraan ja muuttele taulukon rajoja ja askelta. Kaiken tämän voit hyvin tehdä suoraan komentoikkunassa, selaamalla komentopuskuria tarpeen mukaan "nuoli ylös"-näppäimella.

Muista, että Matlabissa ei ole Maplen tapaan vapaita muuttujia. Niinpä et voi etukäteen kirjoittaa laskentakaavaa, vaan C-vektorin on oltava olemassa ennen kaavan käyttöä. Tästä myös seuraa, että F ei päivity automaattisesti (kuten Maplessa), vaan aina, kun C-vektoria muutetaan, on haettava komentopuskurista F-kaava ja annettava sille ENTER:iä.