MattieT/mlteht/mlNonlinEqu
Contents
mlNl005R
Tarkastellaan yhtälöä

- Osoita, että yhtälöllä on yksikäsitteinen ratkaisu avoimella välillä
 .
. - Piirrä kummankin puolen kuvaaja samaan kuvaan etsiäksesi sopivan alkuarvon x0.
- Ratkaise yhtälö numeerisesti Matlab-funktiolla fzero
- Myos Newtonin menetelmalla funktiolla myNewton tms., jos on annettu aiemmin ohjelmoitavaksi (tai annetaan valmiina)
Ratkaisu
(a)
Erotuksella eri merkit lähellä päätepisteitä ==> Erotuksella nollakohta. Toinen on kasvava, toinen pienenevä, joten erotus monotoninen ==> ratkaisu yksikäsitteinen.
(b)
clear
close all
x=linspace(3,4);
plot(x,tan(0.1*x),x,9.2*exp(-x));grid on;shg
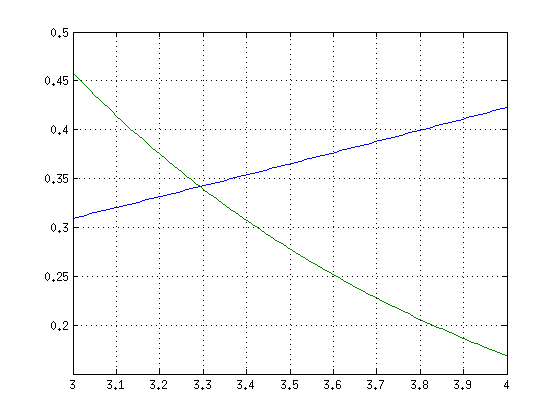
Haetaan funktion f nollakohtaa, missä:
f=@(x) tan(0.1*x)-9.2*exp(-x)
% Alkuarvaus näkyy kuvasta:
f =
@(x)tan(0.1*x)-9.2*exp(-x)
x0=3.3; x1=fzero(f,x0) figure ezplot(f,[3,4])
x1 = 3.292924614900908
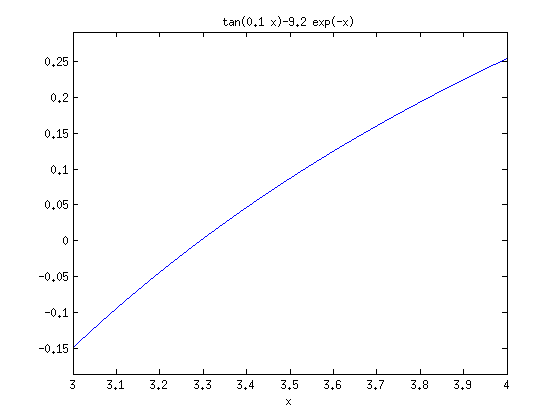
hold on plot(x1,f(x1),'ro');grid on; title(['Ratkaisu = ',num2str(x1)]) shg
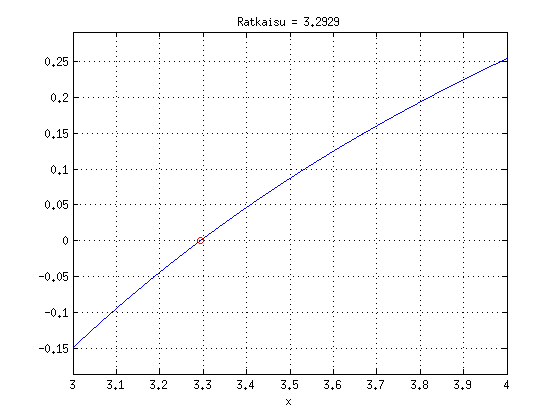
format long
x1
x1 = 3.292924614900908
(d)
help myNewton
Ratkaistaan yhtälö f(x)=0 Newtonin menetelmällä f on funktio ja fder sen derivattafunktio. x0 alkupiste Esim: f=@sin; df=@cos; x0=1; (Kokeile esim. 1.5, 2, 3 jne.) x=myNewton(f,df,x0)
syms x diff(f(x),x) % ans = % (46*exp(-x))/5 + tan(x/10)^2/10 + 1/10
ans = (46*exp(-x))/5 + tan(x/10)^2/10 + 1/10
Maaritellaan funktioksi:
df=@(x)(46*exp(-x))/5 + tan(x/10)^2/10 + 1/10
df =
@(x)(46*exp(-x))/5+tan(x/10)^2/10+1/10
Nyt voidaan soveltaa "myNewtonia":
myNewton(f,df,pi)
ans = 3.292924614900908
Ihmettely: Miksi funktiomäärittelyissä ei tarvita pisteitä?
Vastaus: Koska fzero ja myNewton ovat puhdasta skalaarikoodia. Entä tilanteessa, jossa tarvitaan? Derivaatan lauseke voidaan "pisteyttää" komennolla vectorize.
vectorize-esimerkki:
vectorize(df(x)) % Pisteistä ei koskaan ole haittaa (ellei olla suorittamassa % matriisialgebraa), joten aina voidaan varmistella.
ans = (46.*exp(-x))./5 + tan(x./10).^2./10 + 1./10