Alustukset
| > |
with(LinearAlgebra):
with(linalg):
|
Warning, the previous binding of the name GramSchmidt has been removed and it now has an assigned value
Warning, the protected names norm and trace have been redefined and unprotected
| > |
with(plots):setoptions(scaling=constrained):setoptions3d(axes=boxed,orientation=[-30,50]):
|
Warning, the name changecoords has been redefined
| > |
alias(Inv=MatrixInverse,Id=IdentityMatrix,Diag=DiagonalMatrix,Tr=Transpose):
|
| > |
alias(rref=ReducedRowEchelonForm):alias(ref=GaussianElimination):
alias(Id=IdentityMatrix):
|
Määritellään apufunktioita.
Ovat kertakäyttöluonteisia, helposti lennossa modifioitavia.
1. Muotoa [xdata ]
[ydata ]
olevan matriisin määräämien pisteiden polygonipiirto Vastaa Matlabin plot(xdata,ydata) - komentoa.
| > |
piirraM:=dataM->plot(convert(Transpose(dataM),listlist),axes=box,scaling=constrained):
|
| > |
piirraMb:=dataM->plot(convert(Transpose(dataM),listlist),color=blue,axes=box): # Sama sinisellä (värin olis voinut laittaa lisäargumentiksi, mutta näin on vähemmän koodia.)
|
| > |
piirraMr:=dataM->plot(convert(Transpose(dataM),listlist),color=red,axes=box): # Varmuudeksi vielä punaisella, vaikka onkin oletus.
|
Yllä olevat sopivat erilaisten
alueiden kuvautumistehtäviin
.
Seuraavaksi katsotaan yksittäisten vektorien kuvautumista, erityisesti ominaisvektorihavainnollistuksiin.
Funktio
plots[arrow]
mahdollistaa hyvin mainion helpon tavan nuolikuvioon, jossa
sinisellä
annetaan
lähtönuoli
ja
punaisella
sen
kuvanuoli
, kas näin:
| > |
kuvakulma:=(A,u)->display(arrow(u,shape=arrow,color=blue),arrow(A.u,shape=arrow,color=red),scaling=constrained,title="Lahto:sininen, kuva:punainen"):
|
Haluamme katsoa kuvauksen dynamiikkaa animaationa, se käy taas kuin unelma. Jaetaan täyskulma n:ään osaan ja jokaista kohti piirretään sininen yksikkövektori ja sen punainen kuva. Ajetaan animaationa (
insequence=true
).
| > |
nuoletAni:=(A,n)->display(seq(kuvakulma(A,<cos(Theta),sin(Theta)>),Theta=[seq(kkk*2*Pi/n,kkk=0..n)]),insequence=true,scaling=constrained):
|
Joskus on mukavaa (ainakin esteettisesti) katsoa kuvaa staattisesti jättäen kaikki nuolet kuvaan mukaan. Muuten sama, mutta "
insequence=false
"
| > |
nuolikimppu:=(A,n)->display(seq(kuvakulma(A,<cos(Theta),sin(Theta)>),Theta=[seq(kkk*2*Pi/n,kkk=0..n)]),insequence=false,scaling=constrained):
|
Ominaisvektoreiden (ja -arvojen) havainnollistusta nuolikuvin
Yllä määritelty
kuvakulma
ja siihen pohjautuva
nuoletAni
(ja
nuolikimppu
) ovat nyt onnen omiaan.
Esim 1.
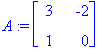
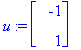
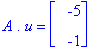
![[Maple Plot]](images/ominaisarvot34.gif)
Valitaan toinen lähtöpiste
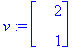
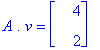
![[Maple Plot]](images/ominaisarvot37.gif)
![[Maple Plot]](images/ominaisarvot38.gif)
No kävipä ihmeellinen sattuman oikku! Lähtö ja kuva osuivat samalle suoralle!!
Jos näin ihmeellisesti käy, sanotaan, että kyseessä on A:n
ominaisvektori
. Kuvan mukaan näyttäisi siltä, että punainen nuoli on n. 2 kertaa sinisen
pituinen. Siinä tapauksessa sanotaan, että vastaava
ominaisarvo
= 2 .
Miten hakisimme yleisemmin? Otetaan (sinisiä)
yksikkövektoreita sopivan tiheästi
ja kuvataan A:lla. Toisin sanoen jaetaan yksikköympyrän kehä
tasavälisesti riittävän hienolla jaolla.
Tässä koodi, jonka kokosimme yllä funktioksi
nuoletAni
| > |
#n:=80:display(seq(kuvakulma(A,<cos(Theta),sin(Theta)>),Theta=[seq(k*2*Pi/n,k=0..n)]),insequence=true,scaling=constrained);
|
![[Maple Plot]](images/ominaisarvot39.gif)
![[Maple Plot]](images/ominaisarvot40.gif)
Tässä näkyy kummankin nuolen rata, mutta ei se, mikä sininen kuvautuu millekin punaiselle. Siispä ominaisvektorit eivät tästä staattisesta kuvasta paljastu. (Mutta esteettistä mielihyvää se voi tuottaa, ja sitäpaitsi ehkä selventää edellisen funktion toimintaperiaatetta.)
Esim 2.
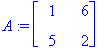
![[Maple Plot]](images/ominaisarvot42.gif)
| > |
piirraM(A.Talo); piirraM(A.ympyra);
|
Plotting error, empty plot
![[Maple Plot]](images/ominaisarvot43.gif)
Nuolet pyörivät nyt vastakkaisiin suuntiin, Toinen ominaissuunta on siinä, missä vektorit ovat päällekkäin, toinen siinä, missä ne ovat vastakkaissuuntaiset.
No lasketaan:
| > |
karpoly:=det(A-lambda*Id(2));Lambda:=solve(karpoly=0,lambda);
|
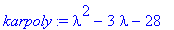
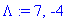
| > |
Eigenvectors(A); # Katsotaan valmiilla funktiolla.
|
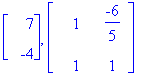
Ominaisvektoria [1,1] matriisi A venyttää kertoimella 7 ja vektoria [-6,5] kertoimella 4, miinus-merkki tarkoittaa, että vektorit ovat vastakkaissuuntaiset.
Tarkistetaan vielä:
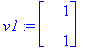
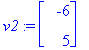
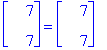
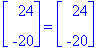
Niinpä on!
| > |
N:=50: h:=2*Pi/N:t:=seq(k*h, k=1..N+1):x:=map(cos,[t]): y:=map(sin,[t]):
|
| > |
display(piirraM(A.ympyra),piirraMb(ympyra),arrow([7*v1/norm(v1,2),4*v2/norm(v2,2)],scaling=constrained,shape=arrow));
|
![[Maple Plot]](images/ominaisarvot51.gif)
Sininen yksikköympyrä, punainen kuvaellipsi, yksikköominaisvektorien kärjet ovat nuolien ja sinisen ympyrän leikkauspisteissä, ominaisarvoilla kerrottuna ne
yltävät ellipsin kehälle puoliakselien kohdalla.
Esim 3
Onko kiertokuvauksella ominaisarvoja/vektoreita?
| > |
A:=<<cos(phi),sin(phi)>|<-sin(phi),cos(phi)>>;
|
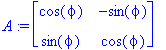
| > |
phi:=Pi/4:nuoletAni(A,40);
|
![[Maple Plot]](images/ominaisarvot53.gif)
No ei sitten millään voi olla ominaisarvoja, nuolet pyörivät samaa vauhtia, eivätkä missään mene päällekkäin.
Mutta mutta ... mehän sallimme myös kompleksiset skalaarit. Kompleksikertlaskuhan on tason kiertoa!
Lasketaanpa!
| > |
karpoly:=det(A-lambda*Id(2));
|
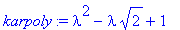
| > |
lam:=solve(karpoly=0,lambda);
|
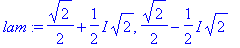
| > |
M1:=A-lam[1]*Id(2);rM1:=ref(M1);
|
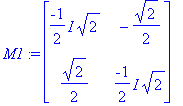
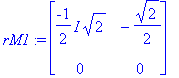
| > |
x2:=t: x1:=solve(rM1[1,1]*x+rM1[1,2]*x2=0,x);
|
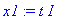
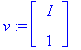
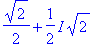
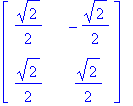
| > |
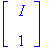
A.v,map(evalc,lam[1].v);
|
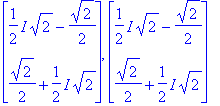
Samoja ovat, joten oikein laskettiin. Toinen ominaisarvo/vektori saadaan kompleksikonjugoimalla.
Kysymys
: Onko nyt niin, että joko nuolet menevät jossain päällekkäin (reaaliset ominaisarvot) tai kyseessä on kierto.
Vastaus:
Kyllä, paitsi kiertoon voi yhdistyä venytys/kutistus (kertominen reaalisella skalaarilla).
Onko tässä siis kaikki
, mitä 2 x 2-matriisesita voidaan yleisesti sanoa?
Eipä olekaan!
Kukaan ei ole sanonut, että ominaisvektoreita on aina kaksi lineaarisesti riippumatonta.
No onko vai ei?
| > |
A1:=<<1,0>|<1,1>>; #A2:=<<1,1>|<-1,-1>>; A3:=<<0,0>|<1,0>>;
|
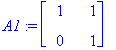
| > |
karpoly1:=det(A1-lambda*Id(2));#karpoly2:=det(A2-lambda*Id(2));karpoly3:=det(A3-lambda*Id(2));
|
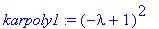
![[1, 2, {vector([1, 0])}]](images/ominaisarvot68.gif)
Tämä tarkoittaa, että A1:n ominaisrvo 1 on kaksinkertainen (senhän jo näimme edellä), ja sillä on vain yksi LRT ominaisvektori [1,0]. Tutkitaanpa:
![[Maple Plot]](images/ominaisarvot69.gif)
Huomataan, että nuolet menevät kaksi kertaa samalle suoralle, mutta kyseessä on sama x-akseli kummallakin kertaa. Sillä perusteella on vain yksi LRT ominaisvektori. Tässä tapauksessa mistään kompleksikosmoksesta ei voi tipahtaa ylimääräisiä ominaisvektoreita, sillä kompleksitapauksessa kaksinkertainen ominaisarvo ei ole mahdollinen. (Miksi?)
| > |
piirraM(A1.ympyra); # Vertaa tätä edelliseen animaatioon, niin ymmärrät. Nyt ei max venymä/kutistuma edustakaan ominaisarvoa.
|
![[Maple Plot]](images/ominaisarvot70.gif)
Kysymys: Ovatko ellipsin puoliakselivektorit hyödyllisiä, miten ne liittyvät yleisiin lineaarialgebrakäsitteisin?
![[Maple Plot]](images/ominaisarvot71.gif)
Tämä kuva on kaunis, mutta siitä ei näe, mikä sininen kuvautuu millekin punaiselle.
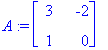
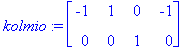
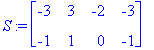
![[Maple Plot]](images/ominaisarvot4.gif)
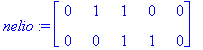
![[Maple Plot]](images/ominaisarvot6.gif)
![[Maple Plot]](images/ominaisarvot7.gif)
![[Maple Plot]](images/ominaisarvot8.gif)
![[Maple Plot]](images/ominaisarvot9.gif)
![[Maple Plot]](images/ominaisarvot10.gif)
![[Maple Plot]](images/ominaisarvot11.gif)
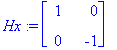
![[Maple Plot]](images/ominaisarvot13.gif)
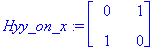
![[Maple Plot]](images/ominaisarvot15.gif)
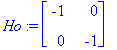
![[Maple Plot]](images/ominaisarvot17.gif)
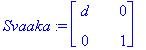
![[Maple Plot]](images/ominaisarvot19.gif)
![[Maple Plot]](images/ominaisarvot20.gif)
![]()
![[Maple Plot]](images/ominaisarvot22.gif)
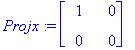
![[Maple Plot]](images/ominaisarvot24.gif)
![]()
![[Maple Plot]](images/ominaisarvot26.gif)
![[Maple Plot]](images/ominaisarvot27.gif)
![[Maple Plot]](images/ominaisarvot28.gif)
![[Maple Plot]](images/ominaisarvot29.gif)
![[Maple Plot]](images/ominaisarvot30.gif)
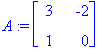
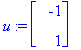
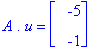
![[Maple Plot]](images/ominaisarvot34.gif)
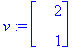
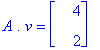
![[Maple Plot]](images/ominaisarvot37.gif)
![[Maple Plot]](images/ominaisarvot38.gif)
![[Maple Plot]](images/ominaisarvot39.gif)
![[Maple Plot]](images/ominaisarvot40.gif)
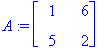
![[Maple Plot]](images/ominaisarvot42.gif)
![[Maple Plot]](images/ominaisarvot43.gif)
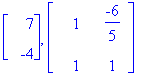
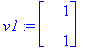
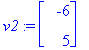
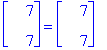
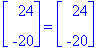
![[Maple Plot]](images/ominaisarvot51.gif)
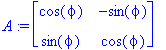
![[Maple Plot]](images/ominaisarvot53.gif)
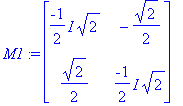
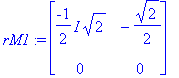
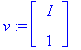

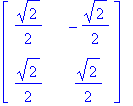
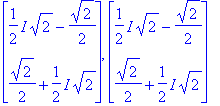
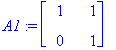
![[Maple Plot]](images/ominaisarvot69.gif)
![[Maple Plot]](images/ominaisarvot70.gif)
![[Maple Plot]](images/ominaisarvot71.gif)