Euler, Heun, eli parannettu Euler (RK2)
Esim 1 y' = t+y
| > | restart: |
| > | with(plots): |
Warning, the name changecoords has been redefined
| > | f:=(t,y)->t+y; # Diff. yhtälön määrittelevä funktio f(t,y) |
![]()
| > | h:=0.4:T[0]:=0:y[0]:=0: N:=3: # Alkuasetukset. |
| > | T[1]:=T[0]+h; y[1]:=y[0]+h*f(T[0],y[0]); # 1. Euler-askel |
![]()
![]()
| > | T[2]:=T[1]+h; y[2]:=y[1]+h*f(T[1],y[1]); # 2. Euler-askel |
![]()
![]()
Nyt riitti manuaalinen toiminta. Aloitetaan alusta ja rakennetaan for-silmukka.
| > | h:=0.4:T[0]:=0:y[0]:=0: N:=3: # Alkuasetukset uudestaan. |
| > | for k from 0 to N do T[k+1]:=T[k]+h; y[k+1]:=y[k]+h*f(T[k],y[k]) end do: |
| > | polku1:=[seq([T[k],y[k]],k=0..N)]; # Tässä ovat pisteet [t[k],y[k]]: |
![]()
| > | plot(polku1,axes =box,legend="h=0.4"); |
![[Maple Plot]](images/dynumer7.gif)
| > | Ekuva1:=%: |
| > | h:=h/2;T[0]:=0;y[0]:=0: N:=2*N; # Puolitetaan askel h ja kaksinkertaistetaan N. |
![]()
![]()
![]()
| > | for k from 0 to N do T[k+1]:=T[k]+h: y[k+1]:=y[k]+h*f(T[k],y[k]) end do: |
| > | polku2:=[seq([T[k],y[k]],k=0..N)]: plot(polku2,color=green,axes=box,legend="h=0.2"); Ekuva2:=%: |
![[Maple Plot]](images/dynumer11.gif)
| > | h:=h/2;T[0]:=0;y[0]:=0: N:=2*N; T1:=N*h; # Ja vielä kerran. |
![]()
![]()
![]()
![]()
| > | for k from 0 to N do T[k+1]:=T[k]+h: y[k+1]:=y[k]+h*f(T[k],y[k]) end do: |
| > | polku3:=[seq([T[k],y[k]],k=0..N)]; plot(polku3,color=blue,axes=box,legend="h=0.1"); Ekuva3:=%: |
![]()
![]()
![]()
![]()
![[Maple Plot]](images/dynumer20.gif)
| > | display(Ekuva1,Ekuva2,Ekuva3,title="Eulerin polut"); |
![[Maple Plot]](images/dynumer21.gif)
Katsotaan kunkin polun viimeinen y-arvo, eli ratkaisuapproksimaatio pisteessä t=1.2:
| > | yLoppu[1]:=polku1[-1][2];yLoppu[2]:=polku2[-1][2];yLoppu[3]:=polku3[-1][2]; |
| > |
![]()
![]()
![]()
| > |
| > | dsolve({diff(Y(t),t)=t+Y(t),Y(0)=0},Y(t)); |
![]()
| > | ytarkka:=rhs(%); |
![]()
| > | display(Ekuva1,Ekuva2,Ekuva3,plot(ytarkka,t=0..1.2,color=black,legend="Tarkka ratkaisu")); |
![[Maple Plot]](images/dynumer27.gif)
| > | ytarkka12:=eval(subs(t=1.2,ytarkka)); |
![]()
| > | virheet:=seq(ytarkka12-yLoppu[k],k=1..3); |
![]()
Aika lähellä on O(h)-käytös, eli virhe puolittuu, kun askel puolittuu.
Esim. 2 y'=t+y Parannetulla E:lla
| > | #restart: |
| > | with(plots): |
| > | f:=(t,y)->t+y; |
![]()
| > | h:=0.4;T[0]:=0:y[0]:=0: N:=3: |
![]()
| > | for n from 0 to N-1 do s1:=f(T[n],y[n]); s2:=f(T[n]+h,y[n]+h*s1); y[n+1]:=y[n]+h*(s1+s2)/2; T[n+1]:=T[n]+h; end do; |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| > | polku1:=[seq([T[k],y[k]],k=0..N)]; |
![]()
| > | plot(polku1,color=blue,legend="Heun, h=0.4"); |
![[Maple Plot]](images/dynumer45.gif)
| > | Hkuva1:=%: |
| > | display(Ekuva1,Hkuva1,title="Punainen Euler, sininen Heun"); |
![[Maple Plot]](images/dynumer46.gif)
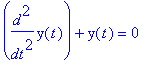
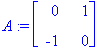
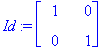
![Y[0] := Vector(%id = 3033508)](images/dynumer50.gif)
![[Maple Plot]](images/dynumer54.gif)
![[Maple Plot]](images/dynumer56.gif)
![[Maple Plot]](images/dynumer58.gif)
![[Maple Plot]](images/dynumer60.gif)