Differentiaaliyhtälöitä Laplace-muunnoksin, osa 2
4.10.2005 HA
Alustukset
| > |
with(inttrans): alias(L=laplace,IL=invlaplace,u=Heaviside):
|
Esim. 1
| > |
with(inttrans): alias(L=laplace,IL=invlaplace,u=Heaviside):
|
| > |
diffyht:=diff(y(t),t,t)+4*y(t)=t*u(t-3);
|
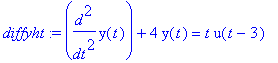
| > |
Ldy:=L(diffyht,t,s); # L-muunnetaan.
|
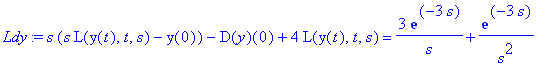
| > |
Ldy:=subs(y(0)=0,D(y)(0)=0,Ldy); # Sijoitetaan alkuehdot.
|
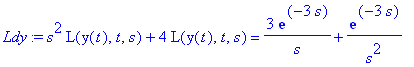
| > |
Y:=solve(Ldy,L(y(t),t,s)); # Ratkaistaan algebr. yhtälö.
|
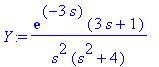
| > |
Yrat:=Y/exp(-3*s); # Otetaan rationaalitekijä käsittelyyn.
|
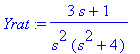
| > |
Yrat:=convert(Yrat,parfrac,s); # Maple muuntaa helposti osamurroksi.
|
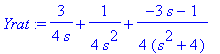
| > |
y:=IL(Yrat*exp(-3*s),s,t); latex(%,a); # Käänteismuunnetaan.
|
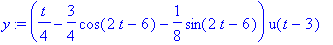
| > |
plot([t*u(t-3),y],t=0..10,color=[red,blue],title="Punainen heräte, sininen vaste",axes=frame);
|
![[Maple Plot]](images/L11LaplaceDY8.gif)
| > |
plot([t*u(t-3),y],t=10..20,color=[red,blue],title="Punainen heräte, sininen vaste",axes=frame);
|
![[Maple Plot]](images/L11LaplaceDY9.gif)
| > |
plot(y,t=0..5,title="Vaste",axes=frame,color=blue);
|
![[Maple Plot]](images/L11LaplaceDY10.gif)
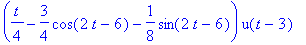
Tutkitaan derivaattojen jatkuvuutta:
| > |
yplus:=(-3/4*cos(2*t-6)-1/8*sin(2*t-6)+1/4*t);
|
| > |
dyplus:=diff(yplus,t);subs(t=3,dyplus): eval(%);
|
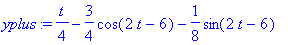
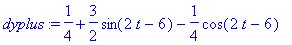
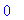
| > |
plot(dyplus*u(t-3),t=0..5,axes=frame);
|
![[Maple Plot]](images/L11LaplaceDY15.gif)
Lasku ja kuva osoittavat, että derivaatta y' on jatkuva, mutta y'' on epäjatkuva 3:ssa. Lasketaan vielä:
| > |
d2yplus:=diff(dyplus,t);subs(t=3,d2yplus): eval(%);
|
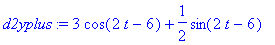
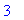
Oikeanpuoleinen y'' on 3 ja vasemmanpuoleinen on 0. Siispä todellakin y'' epäjatkuva (ja sitä ei ole olemassa) pisteessä t=3.
Tämä on tyypillistä: Herätteen epäjatkuvuus ilmenee toisen derivaatan epäjatkuvuutena, alemmat ovat jatkuvia.
Vaimennetun värähtelijän impulssivaste ja delta-approksimointi
| > |
restart:with(inttrans):alias(u=Heaviside,L=laplace,IL=invlaplace):with(plots):#interface(showassumed=2):
|
Warning, the name changecoords has been redefined
| > |
dy:=diff(y(t),t,t)+2*diff(y(t),t)+2*y(t)=Dirac(t);
|
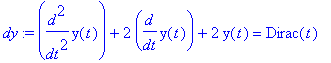
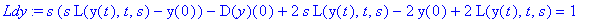
| > |
Ldy:=subs(y(0)=0,D(y)(0)=0,Ldy);
|
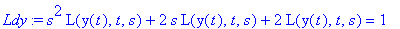
| > |
Y:=solve(Ldy,L(y(t),t,s));
|
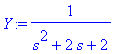
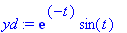
| > |
ydkuva:=plot(yd,t=0..5,color=black,thickness=2):
|
![[Maple Plot]](images/L11LaplaceDY23.gif)
Approksimoidaan Diracin deltaa yksikköimpulssifunktioilla
![delta[epsilon]](images/L11LaplaceDY24.gif) .
.
| > |
delta:=(t,eps)->(u(t)-u(t-eps))/eps;
|
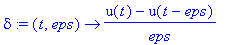
| > |
plot([seq(delta(t,eps),eps=[0.5,0.25,0.1])],t=0..2,color=[blue,green,red]);
|
![[Maple Plot]](images/L11LaplaceDY26.gif)
| > |
dyeps:=diff(y(t),t,t)+2*diff(y(t),t)+2*y(t)=delta(t,epsilon);
|
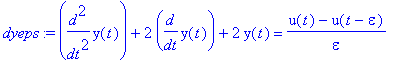
| > |
#Ldyeps:=subs(y(0)=0,D(y)(0)=0,Ldyeps);
|
| > |
#Ye:=solve(Ldyeps,L(y(t),t,s));
|
Yllä olevien automaattisten sijaan suoritetaan enemmän käsinlaskutyylillä.

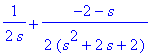
| > |
g:=unapply(IL(%,s,t),t);
|
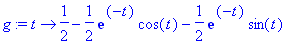
Vaihtoehtoisesti voitaisiin käyttää integraalin muunnosta:
| > |
int(exp(-tau)*sin(tau),tau=0..t);
|
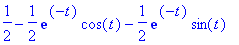
| > |
y:=(t,epsilon)->(g(t)-g(t-epsilon)*u(t-epsilon))/epsilon;
|
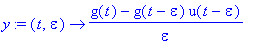
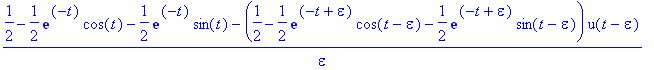
| > |
kuva:=epsilon->plot([delta(t,epsilon),y(t,epsilon)],t=0..5,color=[blue,red],axes=box,title="Sininen herate, punainen vaste");
|
![kuva := proc (epsilon) options operator, arrow; plot([delta(t,epsilon), y(t,epsilon)],t = 0 .. 5,color = [blue, red],axes = box,title =](images/L11LaplaceDY34.gif)
| > |
#display(seq(kuva(1/k),k=1..10),insequence=true,view=[0..5,0..1]);
|
| > |
ydkuva:=plot(yd(t),t=0..5,color=black,thickness=2):
|
| > |
display(seq(kuva(1/(2^k)),k=1..7),insequence=true,view=[0..5,-0.1..1]);
|
![[Maple Plot]](images/L11LaplaceDY35.gif)
| > |
display(seq(kuva(1/(2^k)),k=1..7),ydkuva,insequence=false,view=[0..5,-0.1..1]);
|
![[Maple Plot]](images/L11LaplaceDY36.gif)
![[Maple Plot]](images/L11LaplaceDY37.gif)
Konvoluutioratkaisu
| > |
restart:with(inttrans):alias(u=Heaviside,L=laplace,IL=invlaplace):with(plots):
|
Warning, the name changecoords has been redefined
| > |
dy:=diff(y(t),t,t)+3*diff(y(t),t)=r(t);
|
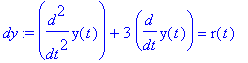
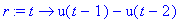
![[Maple Plot]](images/L11LaplaceDY40.gif)
| > |
Q:=convert(1/s/(s+3),parfrac,s);
|
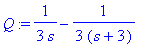
| > |
q:=unapply(IL(Q,s,t),t);
|
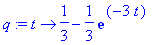
Ratkaisu 1:
Lasketaan "käsin", annetaan Maplen vain tehdä rutiini-integroinnit:
| > |
y=Int('r(tau)'*'q(t-tau)',tau=0..t);
|
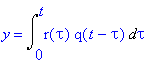
1) 0 < t < 1. Tällöin
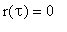 ja siis y(t)=0.
ja siis y(t)=0.
2) 1 < t < 2 Nyt
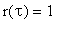 , joten
, joten
| > |
y=Int('q(t-tau)',tau=1..t);
|
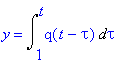
| > |
y=int(q(t-tau),tau=1..t);
|
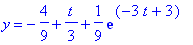
3) t > 2. Nyt integroidaan väli 1..2 kokonaan:
| > |
y=Int('q(t-tau)',tau=1..2);
|
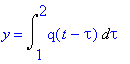
| > |
y=int(q(t-tau),tau=1..2);
|
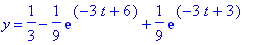
Tässä siis tulos. Kerätään vielä yhteen antamalla Maplen ensin integroida suoraan ja ...
| > |
yy:=int(r(tau)*q(t-tau),tau=0..t);
|
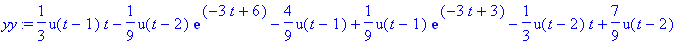
... sitten antamalla sen muuntaa Heaviside-esitys paloittain määritellyksi "piecewise"- esitykseksi:
Kutsutaan täsä
ratkaisuksi 2
:
![PIECEWISE([0, t < 1],[undefined, t = 1],[-4/9+1/3*t+1/9*exp(-3*t+3), t < 2],[undefined, t = 2],[1/3-1/9*exp(-3*t+6)+1/9*exp(-3*t+3), 2 < t])](images/L11LaplaceDY51.gif)
Ratkaisu 3
: Ilman konvoluutiota (vanhoin keinoin)
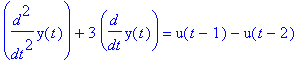
| > |
Ldy:=subs(y(0)=0,D(y)(0)=0,L(dy,t,s));
|
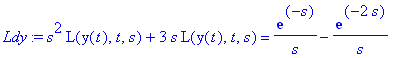
| > |
Y:=solve(Ldy,L(y(t),t,s));
|
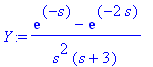
| > |
yik:=IL(Y,s,t); # "y-ilman-konvoluutiota"
|
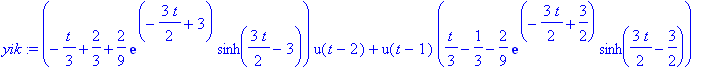
| > |
plot([yy,yik+0.002],t=0..5); # Nostetaan toista hiukan (0.002), jotta erottuisivat.
|
![[Maple Plot]](images/L11LaplaceDY56.gif)
| > |
convert(yik,exp): simplify(%); convert(%,piecewise);
|
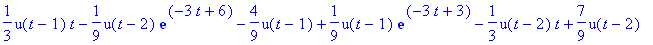
![PIECEWISE([0, t < 1],[undefined, t = 1],[-4/9+1/3*t+1/9*exp(-3*t+3), t < 2],[undefined, t = 2],[1/3-1/9*exp(-3*t+6)+1/9*exp(-3*t+3), 2 < t])](images/L11LaplaceDY58.gif)
| > |
plot([r(t),yy],t=0..5);
|
![[Maple Plot]](images/L11LaplaceDY59.gif)
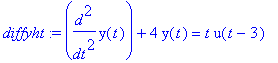
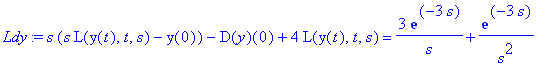
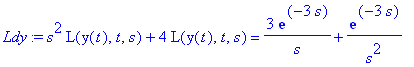
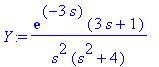
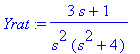
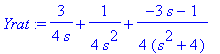
![]()
![[Maple Plot]](images/L11LaplaceDY8.gif)
![[Maple Plot]](images/L11LaplaceDY9.gif)
![[Maple Plot]](images/L11LaplaceDY10.gif)
![]()
![]()
![]()
![]()
![[Maple Plot]](images/L11LaplaceDY15.gif)
![]()
![]()
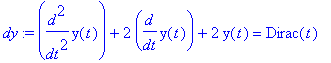
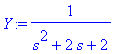
![[Maple Plot]](images/L11LaplaceDY23.gif)
![[Maple Plot]](images/L11LaplaceDY26.gif)
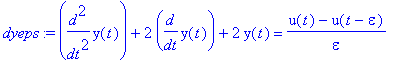

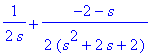
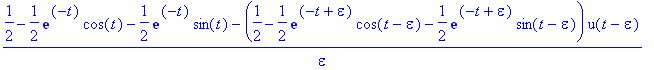
![[Maple Plot]](images/L11LaplaceDY35.gif)
![[Maple Plot]](images/L11LaplaceDY36.gif)
![[Maple Plot]](images/L11LaplaceDY37.gif)
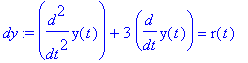
![[Maple Plot]](images/L11LaplaceDY40.gif)
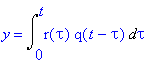
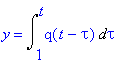
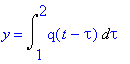
![PIECEWISE([0, t < 1],[undefined, t = 1],[-4/9+1/3*t+1/9*exp(-3*t+3), t < 2],[undefined, t = 2],[1/3-1/9*exp(-3*t+6)+1/9*exp(-3*t+3), 2 < t])](images/L11LaplaceDY51.gif)
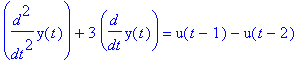
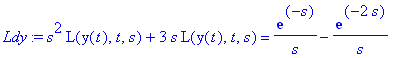
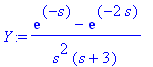
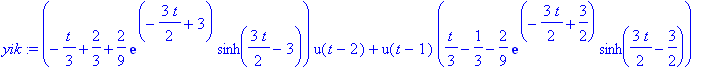
![[Maple Plot]](images/L11LaplaceDY56.gif)
![PIECEWISE([0, t < 1],[undefined, t = 1],[-4/9+1/3*t+1/9*exp(-3*t+3), t < 2],[undefined, t = 2],[1/3-1/9*exp(-3*t+6)+1/9*exp(-3*t+3), 2 < t])](images/L11LaplaceDY58.gif)
![[Maple Plot]](images/L11LaplaceDY59.gif)