Teht.5

Lämpöyhtälö: ut=a2uxx
Reunat = 0
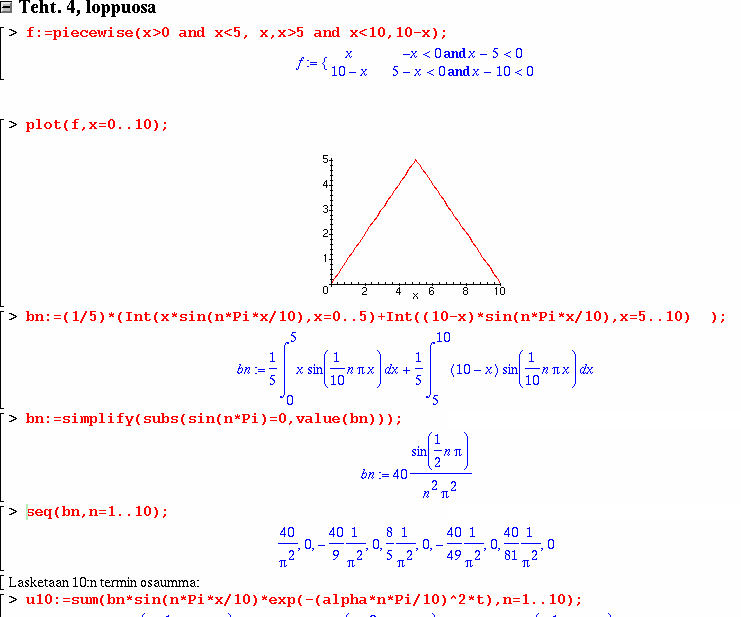
Alkuehto: u(x,0)=x,   väl.  (0,5)
                10-x, väl.  (5,10)

L=10  

Yrite: u(x,t)=X(x)T(t), sij. lämpöyhtälöön:

==>                     X''    T'
                        --- =  -- = -p2  (vakio)
                         X    a2 T
=>  X'' + p2 X = 0
    T' = -a2p2 T

=> X(x)=A cos px + B sin px, T=C exp(-a2p2 t)

RE1: 0=X(0)=A
RE2: 0=X(Pi)=B sin(p L)  => p=pn=n Pi/L

un(x,t)=bn sin pnx exp(-a2pn2 t)

Näiden summa tot. lämpöyhtälön ja RE:t, siten 

                        infinity
                         -----
                         \                          
             u(x,t)  =    )     bn sin(n Pi x/L) exp(-(a n Pi/L)2  t)
                         /
                         -----
                         n = 1

toteuttaa myös (kun termeittäin derivoinnin luvallisuus uskotaan).

AE:
=== 

                             infinity
                               -----
                                \                   
                   u(x,0)  =     )     bn sin(n Pi x/L)
                                /
                               -----
                               n = 1
Siis, kun valitaan bn:t annetun alkuarvofunktion f(x) Fourier-sinisarjan
kertoimiksi (väl. [0,L]), saadaan AE:kin toteutumaan: