Harj. 9 AV teht. 1

20.11.2005  HA

1.

>    restart:

>    with(LinearAlgebra):with(linalg): 

Warning, the previous binding of the name GramSchmidt has been removed and it now has an assigned value



Warning, the protected names norm and trace have been redefined and unprotected

>    A:=<<1,9>|<-1,-5>>;

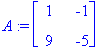
A := Matrix(%id = 17944116)

Harj. 9 AV tehtävässä 3 saatiin HY:n  yleinen  ratkaisu y(t) = c1*y1(t)+c2*y2(t) , otetaan siitä (eräs) perusmatriisi latomalla y1(t) ja y2(t)

sarakkeiksi. Näin saadaan:

>    Y:=exp(-2*t)*<<1,3>|<t,3*t-1>>;

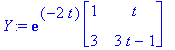
Y := exp(-2*t)*Matrix(%id = 18009652)

Luennolla esitetyn määritelmän mukaan:

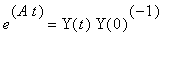
                                                                       e^(A*t) = Y(t)*Y(0)^(-1)

>    Y0:=eval(subs(t=0,Y));Y0I:=MatrixInverse(Y0);

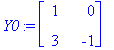
Y0 := Matrix(%id = 18082496)

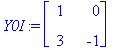
Y0I := Matrix(%id = 18104108)

>    E:=t->exp(-2*t)*(<<1,3>|<t,3*t-1>>.Y0I);

E := proc (t) options operator, arrow; exp(-2*t)*(`<|>`(`<,>`(1,3),`<,>`(t,3*t-1)).Y0I) end proc

>    E(t);

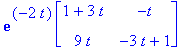
exp(-2*t)*Matrix(%id = 18160672)

Tarkistetaan ja todetaan, että oikein meni:

>    Matrix(exponential(A,t));

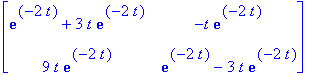
Matrix(%id = 18421044)

Sitten lasketaan:

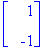
>    y0:=<1,-1>;   # Alkuehto

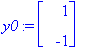
y0 := Vector(%id = 18221108)

>    yh:=E(t).y0;  # (HY):n osuus

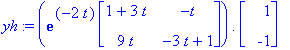
yh := exp(-2*t)*Matrix(%id = 18665184).Vector(%id = 18221108)

>    yh:=exp(-2*t)*((<<1,3>|<t,3*t-1>>.Y0I).y0);  # Sievenettynä

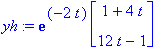
yh := exp(-2*t)*Vector(%id = 18797936)

(EHY)-osuus:

>    EHYintgroitava:=map(simplify,E(t-s).<s,1>);

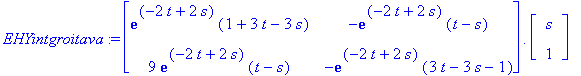
EHYintgroitava := Matrix(%id = 18992868).Vector(%id = 18906668)

>    yp:=map(int,EHYintgroitava,s=0..t);   # (EHY):n erikoinen

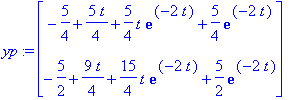
yp := Vector(%id = 18906708)

                                                 

>    y:=yh+yp;  y:=simplify(%);               # Tässä koko ratkaisu.

>   

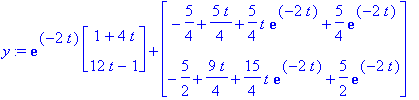
y := exp(-2*t)*Vector(%id = 18797936)+Vector(%id = 18906708)

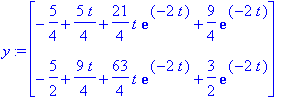
y := Vector(%id = 20967452)

Tarkistus:

>    subs(t=0,y);

Vector(%id = 2484704)

>    vasen:=map(diff,y,t);

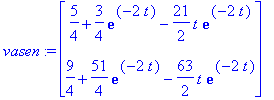
vasen := Vector(%id = 2490288)

>    oikea:=A.y+<t,1>;

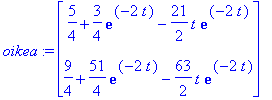
oikea := Vector(%id = 2572660)

>