|
Rakenne: Kaikkein perustavin asia sijoitetaan yhteen tiedostoon, "ylimmän tason" viitteet ovat siten sisäisiä linkkejä. Lisäpiirteet ovat omissa tiedostoissaan. Tämä helpottaa perusoppaan paperitulostusta ja säästää paperia, erityispiirteitä voi itsekukin tulostella tarpeen mukaan.
Tässä kappaleessa (ensi)esiintyvät Matlab-komennot
Sanomme tarkoituksellisesti saman asian monessa eri paikassa, jotta lukija välttyisi ylenmääräiseltä selailulta. (Joskus tällaista voi sattua vahingossakin, mutta sitä emme myönnä.)
Matlab-työskentelyn dokumentoinnissa noudatamme seuraavanlaista käytäntöä:
Osa 1. Alkuunpääsy |
|
|---|---|
0. Johdanto
|
1. Käynnistys, työtila, avustus>> help , doc >> u=[1 2 3] % vaakavektori >> v=[1;2;3] % pystyvektori >> A=[1 2 3;4 5 6] % matriisi >> path, addpath |
2. Vektorit ja matriisit
| |
0. Johdanto |
1. Käynnistys, työtila, avustus>> help , doc >> u=[1 2 3] % vaakavektori >> v=[1;2;3] % pystyvektori >> A=[1 2 3;4 5 6] % matriisi >> path, addpath |
2. Ensiaskeleet vektoreilla ja matriiseilla
|
|
3. Matriisi- ja taulukko-operaatiot 3.1 Työtila, muuttujat, istunnon talletus, help 3.2 Laskentatarkkuus, tulostusasu, aritmetiikkaa |
4. Muuttujat ja lausekkeet, vertailua Mapleen | 5. Matriisien osat ja kokoaminen matriisifunktioita |
| 6. Ohjausrakenteita: for, while, if | 7. Skalaarifunktiot | 8. Vektorifunktiot |
Cleve Moler kirjoitti alkuperäisen Matlabin Fortran-version 1970-luvun loppupuolella pienimuotoiseksi matriisilaskennan opetusohjelmaksi. Kyseessä oli Fortranilla kirjoitettu matriisitulkki, joka käytti LINPACK- ja EISPACK- kirjastojen rutiineja laskentakoneenaan. Vaiheita:
Esikuvia kielelle: "Speak Easy" ja APL (Kenneth Iverson 1960-luvulla, Jim Brown, IBM Yorktown Heights: APL2 1984, ...)
Nykyisin : "Teollisuusstandardin asemassa", suuri määrä ammattimaisia toolboxeja.
Matlab on saatavissa kaikkiin ajateltavissa oleviin käyttöjärjestelmiin. Matlab-koodit ja työtilat talletetaan tekstimuodossa, mikä takaa ongelmattoman siirrettävyyden eri ympäristöjen välillä.
Matlab-ohjelman lisenssin omistaa The MathWorks, Inc., www.mathworks.com
matlab tai kaksoisklikkaamalla Matlab-ikonia.
use matlab matlabOhjelma lopetetaan komennolla
>> quittai sulkemalla hiirellä Matlab-ikkuna.
< M A T L A B >
Copyright 1984-1999 The MathWorks, Inc.
Version 5.3.0.10183 (R11)
Jan 21 1999
To get started, type one of these: helpwin, helpdesk, or demo.
For product information, type tour or visit www.mathworks.com.
Ohjelman käynnisttyttyä, tulkki antaa kehotteen >> . Tällöin sille
voidaan kirjoittaa Matlab-komentoja.
>> v=[1; 2; 3] % Muodostetaan pystyvektori v
v =
1
2
3
>> A=[1 -1 0;2+3*i 4.5 7;5 6 -1] % Muodostetaan 3 x 3-matriisi A
A =
1.0000 -1.0000 0
2.0000 + 3.0000i 4.5000 7.0000
5.0000 6.0000 -1.0000
>> A*v % Matriisi kertaa vektori
ans =
-1.0000
32.0000 + 3.0000i
14.0000
|
Mitä opimme:
Pienimuotoista Matlab-laskentaa voi harrastaa komentoikkunassa. Komentoja voi selata nuoli-ylös-näppäimellä samaan tapaan kuin Unix:n tcshellissä ja komentoriviä voi editoida.
Vähänkin vakavampihenkinen työskentely kannattaa järjestää erillistä editori-ikkunaa hyödyntäen. Komennot voidaan kirjoittaa tekstitiedostoon, vaikkapa komennot.m. Kun tiedoston nimi (ilman m-tarkennetta) kirjoitetaan Matlab- komentoikkunassa, tulkki suoritettaa komennot, aivan kuin ne kirjoitettaisiin peräkkäin Matlab-istuntoon. Siis >> komennot (tällöin on vain huolehdittava siitä, että tiedosto on joko työhakemistossa tai Matlab-polun (path) varrella. Vaihtoehtoisesti komennot voidaan koota tekstitiedostoon doku.txt tai vaikkapa doku.html. Tällöin tiedostossa olevia komentoja voidaan leikkaus/liimaus-hiirioperaatiolla siirtää komentoikkunan ja dokumentin välillä.
Komentojonotiedostoja kutsutaan lyhyesti skripteiksi. Skriptit ja funktiotiedostot ovat yhteiseltä nimeltään m-tiedostoja, molemmat ovat tyyppiä tied.m olevia tekstitiedostoja. Funktiotiedosto alkaa avainsanalla function ja se toimii, kuten funktion kuuluu: sille annetaan syöteparametreja, ja se palauttaa yhden tai useamman tulosarvon.
M-tiedostoja käsitellään lähemmin kohdassa 14
help, helpwin, helpdesk, lookfor
who - muuttujien nimet whos - lisäksi koko- ja talletusinformaatio clear - työtilan muuttujien vapauttaminen arvoistaanKomennon keskeytys : CTRL-C
Vektoreita ja skalaareja voidaan pitää erikoistapauksina matriisista, viimemainittu on 1 x 1 - matriisi. Tästä ajattelusta seuraa, että rivivektorit ja sarakevektorit erotellaan toisistaan, edelliset ovat 1 x n - ja jälkimmäiset n x 1 - kokoisia matriiseja, missä n on vektorin pituus.
Versiosta 5 alkaen Matlabissa on myös sisäkkäisiä ja moniulotteisia rakenteita.
Matriiseja voidaan luoda eri tavoilla:
>> A = [1 2 3; 4 5 6; 7 8 9]Matlab näyttää komennon tuloksen tai muuttujan sisällön (jota emme tässä kuitenkaan näytä), ellei komentoa päätetä puolipisteellä.
Rivien erottimena on puolipiste, rivin alkioiden erottimena voidaan käyttää
tyhjän ohella myös pilkkua. Rivierottimena käy myös rivinvaihto, selkeämpää
lienee tällöin kirjoittaa myös puolipiste.
Sama matriisi voitaisiin siten
kirjoittaa vaikkapa näin:
>> A = [1 2 3; 4 5 6; 7 8 9];Tässä päätimme komennon puolipisteeseen, joten Matlab-tulkki ei tulosta ruudulle matriisin A sisältöä. Otamme pienen esimerkki-istunnon vektoreista.
>> format compact % Tulostusasua säätelevä komento.
>> v=[1 2 3 4 5] % v=[1,2,3,4,5] % Pilkut käyvät myös.
v =
1 2 3 4 5
>> v=1:5; % Sama vektori saadaan kätevämmin näin.
% help colon (lähemmin kohdassa 11)
>> vt=v' % Transponoidaan pystyvektoriksi.
vt =
1
2
3
4
5
>> [1;2;3;4;5] % Pystyvektori voidaan luoda myös suoraan.
ans = % Tässä emme sijoita sitä arvoksi millekään
1 % muuttujalle. Matlab antaa sille nimen ans,
2 % johon voidaan viitata, kuten mihin tahansa
3 % muuttujaan. Tämä pätee vain viimeksi suoritettuun
4 % komentoon. (Vrt. Maplen %)
5
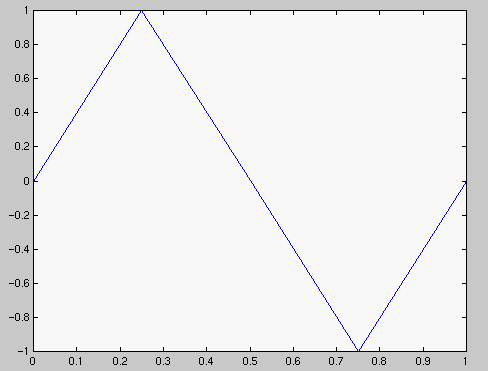
Halutkaamme piirtää funktio f(x)=sin(2*pi*x) välillä
[0,1].
Tarvitsemme
>> x=[0 0.25 0.5 0.75 1] % Havainnollisuuden vuoksi harva pisteistö.
x =
0 0.2500 0.5000 0.7500 1.0000
>> y=sin(2*pi*x) % sin-funktio operoi jokaiseen x-vektorin
% komponenttiin (skaalarifunktio)
y =
0 1.0000 0.0000 -1.0000 -0.0000
>> [x' y'] % Pisteparien taulukko saadaan laittamalla pystyyn
% transponoidut vektorit vierekkäin 2-sarakkeiseksi
% matriisiksi.(Tämä vain asian havainnollistamiseksi)
ans =
0 0
0.2500 1.0000
0.5000 0.0000
0.7500 -1.0000
1.0000 -0.0000
>> plot(x,y) % Yhdistetään edellä olevat (x,y)-parit murtoviivalla.
|

|

|
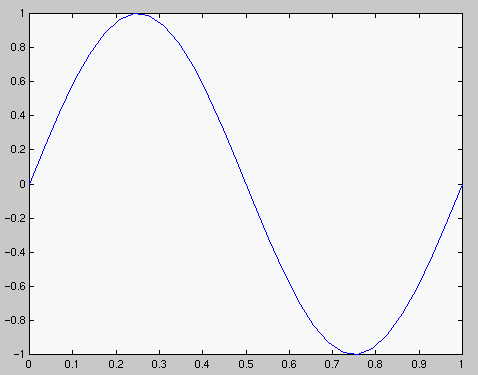
| Jako 4:ään osaväliin | Jako 29:ään osaväliin |
Tarkemman kuvan saamme jakamalla välin hienommin. Tähän on kaksi oivallista tapaa, joko muoto x=0:0.1:1; tai x=linspace(0,1,30); Kokeile tai lue lisää (tai help colon, help linspace) (Kaksoispiste on englanniksi "colon".) Homma hoituu näin:
>> x=linspace(0,1,30); y=sin(2*pi*x); plot(x,y)
>> A=vander([1 2 3]) % Vandermonden matriisi on ei-singulaarinen,
% Matlabissa on valmis funktio sen muodostamiseen.
>> B=inv(A)
>> A*B % Katsotaan, onko B tosiaan käänteismatriisi.
>> A*B-eye(size(A)) % Yleisemmin voidaan samuutta testata näin.
>> b=[1;1;1] % Haluamme ratkaista systeemin A*x = b .
>> x=B*b % Kerrotaan käänteismatriisilla.
>> x=A\b % Tehokkaampi tapa on käyttää \-operaatiota.
% Muistisääntö: "matriisijako, jossa jakajamatriisi
% on jakoviivan alla.
Muistatko, missä yhteydessä johduttiin Vandermonden matriisiin?
Matriisijakolaskuun saat lisävalaistusta komentamalla help slash , kts. myös ...
Kaksi edellistä on helppo arvata (tai >> help zeros , ... ). >> eye(m,n) tekee m x n - kokoisen osan yksikkömatriisista, ja >> rand(m,n) tekee vastaavasti satunnaisluvuista koostuvan matriisin, viimeiseksi mainittu primes muodostaa alkulukuvektorin. Tutustumme näihin sekä moniin muihin aikanaan lähemmin.
Matriisien rakenteluun voidaan käyttää tehokkaasti myös isojen matriisien kokoamista pienemmistä osista, for-silmukoita, meshgrid- komentoa, sparse-alkuisia harvojen matriisien luontikomentoja jne. ( section 6 Kts).
Vektorin (niin vaaka- kuin pysty) indeksointiin riittää yksi indeksi.
Esim:
>> A=ones(3,4); >> A(2,2)=-1; >> A >> v=-5:5; v(6)Huom: Luvuilla indeksointiin kelpaavat vain positiiviset kokonaisluvut . (Indeksointia loogisilla vektoreilla käsitellään
A(1,:) ilmaisee A-matriisin ensimmäisen rivin (yksinäinen kaksoispiste jälkimmäisenä indeksinä tarkoittaa, että sarakeindeksi käy läpi kaikki arvonsa . Vastaavasti A(:,2) tarkoitta A:n toista saraketta.
Pelkkä kaksoispiste matriisin indeksinä tarkoittaa, että molemmat
indeksit saavat kaikki mahdollset arvonsa. Tällöin tulee tietää, kumpaa
matriisin indeksisuuntaa pidetään ensisijaisena.
Matlab on
sarakeorientoitunut. Tämä johtunee alkuperäisen Matlabin
Fortran-sidonnaisuudesta, mutta siihen on myös relevantteja puhtaasti
matriisilaskennallisia perusteita. (Usein ajattelmme matriisia
kokoelmana vierekkäin ladottuja sarakevektoreita.)
Esim
>> A=reshape(1:12,4,3) % Kätevä tapa muotoilla vektorista matriisi. >> A(:) % Jonoutus sarakkeittain.
Indeksointia ja kaksoispistenotaatiota käsitellään tarkemmin kohdassa 11 ... Kts. myös [SKK] 2.9, ss. 23 - 25.
Komento help elfun antaa alkeisfunktioluettelon ("elementary functios").
Esim.
>> x=linspace(0,5,10) >> y=log(x) % log on luonnollinen logaritmi >> % kokeile vaikka log(exp(1))
Funktio log laskee (luonnollisen) logaritmifunktion arvon jokaisessa x-vektorin komponentissa ( skalaarifunktio).
Piirrä log-funktion kuvaaja välillä (0,5) alkamalla yllä olevasta karkeasta diskretoinnista ja hienontaen sitten vaikkapa jakovölien lukumääriin 20,50,100.
>> clear % Kaikki työtilan muuttujat vapautetaan.
>> x(3)=0 % Matlab varaa 3-pituisen vektorin
x =
0 0 0
>> x(9)=2 % Tilaa varataan automaattisesti lisää.
x =
0 0 0 0 0 0 0 0 2
>> clear A % Varmuustoimenpide
>> A(3,4)=1 % Matriisille varataan oikean kokoinen tila.
A =
0 0 0 0
0 0 0 0
0 0 0 1
Jos tätä tapaa käytetään muuttujan alustuksessa, on siis syytä suorittaa
ensin >> clear x .
Operoitaessa suurilla datamäärillä, on tehokkuussyistä edullista kuitenkin
varata tila ennakkoon. Jos tiedämme tarvitsevamme numeerista vektoria, jonka
pituus on 10 000, on syytä alustaa:
>> x=zeros(1,10000);
Muussa tapauksessa muistinhallinta joutuu
kohtuuttoman kovalle koetukselle.
Havainnollistamme asiaa pienellä esimerkillä, jossa samalla tulee ensi
kosketus Matlabin for-silmukkarakenteeseen .
>> clear x, x(1)=1; for k=1:5, x(k+1)=atan(x(k)), end
x =
1.0000 0.7854
x =
1.0000 0.7854 0.6658
x =
1.0000 0.7854 0.6658 0.5874
x =
1.0000 0.7854 0.6658 0.5874 0.5311
x =
1.0000 0.7854 0.6658 0.5874 0.5311 0.4882
Huomaamme, että muisinhallintajärjestelmä joutuu joka kierroksella
töihin.
[tulos1,tulos2,...] = fun(arg1,arg2,...)Monet funktiot on ohjelmoitu niin, että sekä syöte- että tulosargumenttien lukumäärää voidaan vaihdella.
Jos tulosagumentteja on vain yksi, voidaan vasemalla ovat hakasulut jättää pois.
Esim.
linspace(a,b,n) - funktiossa n=100 on oletus, se on useimmiten sopiva arvo 2-ulotteiseen grafiikkaan, jossa linspace on erityisen tarpeellinen.
>> x=linspace(-pi,pi); % Kolmannen argumentin oletusarvo on 100 >> y=sin(x); >> plot(x,y)Hig: s. 32
>> x=[1 2 3] >> norm(x,2) % Euklidinen normi >> norm(x,1) % l1-normi (itseisarvojen summa) >> norm(x) % Oletusarvona euklidinenTulosargumentit:
>> x=[1 -1 2 -3 4 6] >> m=max(x) >> [m,k]=max(x) % sekä maksimiarvo että sen indeksi.
>> A=rand(6,4); >> koko=size(A) % Palauttaa 2-pituisen vektorin. >> [m,n]=size(A) % Sijoittaa rivien lkm:n muuttujaan m ja >> % sarakkeiden lkm:n muuttujaan n
>> A=rand(5,5); >> eig(A) >> [V,D]=eig(A)
Kertolasku (*) on nimenomaan matriisikertolasku. Jos halutaan laskea kahden samankokoisen matriisin (vektorin) tulo vastinalkioittain (pisteittäin), kirjoitetaan kertomerkin eteen pite (.).
Jakolasku A\B tai A/B tarkoittaa matriisioperaationa yhtälöryhmän ratkaisemista ja taulukko-operaationa (A./B) yksinkertaisesti vastinalkioittain tapahtuvaa jakoa. (Taulukkotapauksessa A.\B on sama kuin A./B) .
Potenssiin korotus A^p tarkoittaa matriisioperaationa tuloa A*A*...*A ja edellyttää siis, että A on neliömatriisi. Taulukko-operaatio A.^B tarkoittaa vastinalkioittain muodostettuja potensseja ja edellyttää samankokoisia matriiseja (joista siis toinen voi olla skalaari).
Kokoamme taulukkoon:
| Laskutoimitus | Matriisioperaatio | Taulukko-operaatio |
|---|---|---|
| Yhteenlasku | + | + |
| Vähnnyslasku | - | - |
| Kertolasku | * | .* |
| Vasemmalta jako | \ | .\ |
| Oikealta jako | / | ./ |
| Potenssi | ^ | .^ |
Vasemman sarakkeen matriisioperaatiot edellyttävät, että operandit ovat oikean kokoisia kyseiseen toimitukseen. Tässäkin tapauksessa skalaarilla operoiminen onnistuu aina. On syytä huomata, että potenssiin korotuksessa ja jakolaskussa matriisi- ja taulukko-operaatiot eivät ole samoja, vaikka toinen argumentti olisi skalaari. Kertolaskussa sensijaan skalaarin ja matriisin tulo on sama kuin pisteittäinen tulo.
>> x=A\bsaamme lineaarisen yhtälösysteemin A*x = b ratkaisuvektorin x . Kyseessä on neliömatriisin A tapauksessa sama asia kuin laskussa
>> x=inv(A)*bTosin käänteismatriisilla kertominen on numeerisen laskennan tehokkuuden ja tarkkuuden kannalta epäedullisempaa.
Tässä b:n on oltava A:n sarakkeen pituinen sarakevektori tai matriisi, jossa tällaisia sarakevektoreita on ladottuna vierekkäin.
Muistisäänöt:
Mainittakoon vielä, että matriisijakolaskussa A:n ei tarvitse olla neliömatriisi. Ellei se ole, ratkaisu suoritetaan PNS-mielessä. (Palataan lähemmin.)
Toisin kuin Maplessa, Matlabissa ei voida käsitellä "vapaita" muuttujia. (Jos käytetään lisäpakkausta "symbolic toolbox", voidaan suorittaa myös symbolisia operaatioita, mutta tässä käsittelemme vain Matlabin perusajatusmaailmaa.)
>> x=[-2,-1,0,3,5]
>> x2=x.^2 % x-vektorin 2. potenssit.
>> x^2 % Matriisipotenssi on tuomittu epäonnistumaan.
>> x.*exp(x) % exp toimii "pisteittäin", kerrotaan exp-arvot
% pisteittäin x-arvoilla.
>> x=linspace(-1,2); % 100-pituinen diskretoitu x-akselin pätkä.
>> plot(x,x.*exp(x)) % Yhdistetään kuvaajan 100-pistettä pikku janoilla.
Tee itsellesi selväksi pisteittäiset, vastinalkioittain toimivat operaatiot.
Esimerkki
rand('state',1)
A=rand(4,4)
[rank(A),rank(A^10),rank(A^25),rank(A^30)]
>> rand('state',1)
>> A=rand(4,4)
A =
0.9528 0.8407 0.0222 0.1996
0.7041 0.4428 0.3759 0.3031
0.9539 0.8368 0.8986 0.5383
0.5982 0.5187 0.4290 0.9102
>> [rank(A),rank(A^10),rank(A^25),rank(A^30)]
ans =
4 4 2 1
Muutaman kokeilun jälkeen näyttää siltä, että välillä [0,1] olevista
satunnaisluvuista koostuvalla neliömatriisilla tapahtuu
rangin putoaminen arvoon 1, kun matriisi korotetaan riittävän korkeaan
potenssiin.
Ilmiötä voidaan analysoida ominaisarvojen avulla erityisesti ns.
Markovin matriisien yhteydessä.
Myös ns. potenssimenetelmä ominaisarvojen numeriikassa liittyy tähän.
clear, CTRL-C, help, helpwin, helpdesk, ... load, diary, saveKertaamme ja täydennämme ensijohdatuksessa sanottua. Ota soveltuvin osin "opas: Työskentely-ystö, help(desk)
Istunnosta saadaan "päiväkirja" tiedostoon "doku" komennolla diary doku. Tämä on tehtävä etukäteen. Usein on kätevämpää menetellä edellisellä tavalla, jotta vältytään kaikenmaailman virheilmoitusten jälkisiivoukselta.
Komentoja save ja load voidaan käyttää, jos halutaan tallettaa kaikki tai osa muuttujista ja palauttaa ne jälkeenpäin levyltä työtilaan. Pelkkä save tallettaa kaikki muuttujat tiedostoon matlab.mat, josta ne saadaan palautetuksi komennolla load. Muuttujien tallettamista tarvittaneen aika harvoin, hyödyllisempää on yleensä tallettaa komennot ja ajaa ne uudestaan.
Sensijaan tyyppiä save 'tiedosto.txt' x y z -ascii olevat
komennot ovat varsin
hyödyllisiä tulosten talletukseen, jos halutaan vaikka jatkaa datan
käsittelyä
jollain muulla ohjelmalla.
Vastaavasti load 'tiedosto.txt' .
Kts. vanhaa L1.html ***
eps, formatHIG s. 35 ieee, NaN, inf
| Matlab | Maple |
|---|---|
| >> muuttuja=lauseke Loppumerkki ei pakollinen (;) estää tulostuksen |
> muuttuja:=lauseke;
Loppumerkki (; tai :) pakollinen, kaksoispiste estää tulostuksen. |
Muuttujan nimissä erotellaan pienet ja isot kirjaimet, siten esimerkiksi x ja X edustavat eri muuttujaa. Tämä pätee niin Maplen kuin Matlabin suhteen. Tuttu englanninkielinen termi "case sensitive" pätee siten molempiin.
Kuten todettu, Matlabissa ei ole vapaita muuttujia, kuten Maplessa. Tämä yksinkertaistaa evaluointimekanismia merkittävästi. Jos evaluonnissa törmätään muuttujaan, jolla ei ole arvoa, saadaan virheilmoitus. (Maplen evaluointisääntöjä on käsitelty mm. viitteessä [HAM].)
Matemaattisten lausekkeiden käsittely on siten Maplessa mukavampaa ja luontevampaa (myös vapaiden muuttujien takia).
Toisaalta Maplessa on tiettyjä komplikaatioita matriisien käsittelyssä. Asia
on paranemaan päin versiossa Maple 6 kehitetyn LinearAlgebra- pakkauksen
ansiosta. Kuitenkin siirtymäkauden hankaluuksia esiintyy, koska nykyisellään on
myös tarvetta vanhempaan linalg-syntaksiin.
Matlab on numeeristen
matriisien käsittelyssä ylivertaisen yksinkertainen ja lisäksi tehokas Mapleen
verrattuna. (Symbolisia matriiseja ei Matlabilla tietenkään voi käsitellä.)
Esimerkki "algebrallisesta" lausekkeesta
x=linspace(-1,1); y1=1+x; y2=y1+(x.^2)/2; y3=y2+(x.^3)/(1*2*3); plot(x,y1,'b',x,y2,'r',x,y3,'g',x,exp(x),'k') >> plot(x,y1,'b',x,y2,'r',x,y3,'g',x,exp(x),'k') >> shg >> grid |
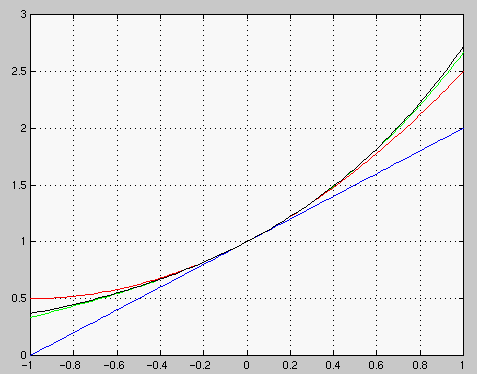
Esimerkki matriisilausekkeesta
>> rand('state',0)
>> A=rand(2,2);
>> S1=eye(2,2)+A;
>> S2=S1+(A^2)/2;
>> S3=S2+(A^3)/(1*2*3);
>> S4=S3+(A^4)/(1*2*3*4);
>> [A,S1,S2,S3,S4,expm(A)]
ans =
Columns 1 through 7
0.9501 0.6068 1.9501 0.6068 2.4716 1.0426 2.6704
0.2311 0.4860 0.2311 1.4860 0.3971 1.6742 0.4642
Columns 8 through 12
1.2187 2.7278 1.2702 2.7441 1.2849
1.7383 0.4838 1.7562 0.4894 1.7613
|
Tulosta on syytä katsoa ajattelemalla sitä vierekkäisinä 2 x 2-matriiseina. Kirjoitetaan yleisemmin for-silmukalla, käytetään samalla uudempaa Matlabin tietorakennetta, solumatriisia, jossa kukin 2 x 2 - matriisi on alkiona "matriisivektorissa" P. (Solumatriisin käyttö ei olisi mitenkään välttämätöntä, sen hyöty tässä yhteydessä on lyhentää laskentakaavaa jakamalla toiminta kahteen for-silmukkaan. Saammepa samalla ensituntuman uuteen tietorakenteeseen (versiossa 5 tulleeseen).
>> for k=1:20; P{k}=(A^k)/prod(1:k); end % Tässä on kätevää käyttää
% solumatriisia P ("cell array")
>> S=eye(2,2);for k=1:20; S=S+P{k}; end
>> [S,expm(A)]
ans =
2.7441 1.2849 2.7441 1.2849
0.4894 1.7613 0.4894 1.7613
>> format long % Täysi tulostustarkkuus
>> [S,expm(A)]
ans =
2.74410134440431 1.28494639715736 2.74410134440431 1.28494639715736
0.48941951062196 1.76130317613298 0.48941951062196 1.76130317613298
>> format short % Palataan alkuperäiseen tulostustarkkuuteen.
|
Huomaa ero x.^k, A^k. Lukija, joka tuntee matriisieksponenttifunktion, huomaa heti mistä on kyse. Sellaiselle lukijalle, joka ei ole tätä käsitettä kohdannut, esimerkki voi avata uusia huikeita näköaloja (?!)
Komentoja, funktioitaeye,zeros,ones,diag,tril, triu, rand, hilb, vander, magic, primes reshape |
>> A=[1 2 1;-1 2 3;-10 -11 -12] >> b=[1;1;1] % tai b=ones(3,1) >> Ab=[A,b] >> A_alle_b=[A;b]Otetaan tässä vertailu Mapleen.
| yhtäsuuri | erisuuri | pienempi | suurempi | pienempi tai yhtäsuuri | suurempi tai yhtäsuuri |
| == | ~= | < | > | <= | >= |
Vertailuoperaattorit voidaan ajatella funktioiksi, joiden argumentit ovat operaattorimerkin molemmin puolin, voidaan puhua vasemmasta ja oikeasta argumentista.
Vertailufunktiot toimivat kohdassa 7 käsiteltävien skalaalaarifunktioiden tavoin.
Tämä tarkoittaa:
>> 2==3, 2<3
ans =
0
ans =
1
Matriisin ja matriisin vertailu >> A=[0 1;2 1],B=ones(size(A)),C=zeros(size(A)),E=eye(2,2)
A =
0 1
2 1
B =
1 1
1 1
C =
0 0
0 0
E =
1 0
0 1
>> A==B
ans =
0 1
0 1
>> A<=C
ans =
1 0
0 0
>> A>E
ans =
0 1
1 0
>> E==(E ~=0)
ans =
1 1
1 1
>> E=(E ~=0) % Pieni kompa: tässä suoritetaan sijoitus muuttujaan E.
E =
1 0
0 1
Skalaarin ja matriisin vertailu >> A=rand(10,10);
>> A>=0.5
ans =
1 0 0 0 1 0 1 0 0 0
0 0 0 1 0 0 0 0 0 0
1 1 1 0 1 0 0 0 1 0
0 1 0 1 1 0 0 0 1 0
0 0 1 1 0 0 1 0 0 1
0 1 1 0 0 0 0 1 0 0
1 1 1 1 1 1 0 1 1 1
1 0 1 0 1 0 1 1 0 0
1 1 0 0 0 0 1 0 1 0
1 0 0 1 1 1 1 1 1 1
Tämä on kätevä tapa selvittää niiden alkioiden paikat, jotka toteuttavat
annetun ehdon (tässä tapauksessa ehtona on " olla >= 0.5 " ).
| ischar | isempty | isequal | isfinite | isieee | isinf |
| isnan | isnumeric | islogical | isprime | issparse |
Lukijaa kehoitetaan kokeilemaan/tutkimaan helpin avulla.
>> luvut10=1:10
luvut10 =
1 2 3 4 5 6 7 8 9 10
>> tosi10=luvut10==luvut10
tosi10 =
1 1 1 1 1 1 1 1 1 1
>> epatosi10=luvut10 ~=luvut10
epatosi10 =
0 0 0 0 0 0 0 0 0 0
>> ykkoset10=ones(1,10)
ykkoset10 =
1 1 1 1 1 1 1 1 1 1
>> nollat10=zeros(1,10)
nollat10 =
0 0 0 0 0 0 0 0 0 0
>> isnumeric(tosi10)
ans =
1
>> islogical(ykkoset10)
ans =
0
>> tosi10-tosi10
ans =
0 0 0 0 0 0 0 0 0 0
>> isequal(ans,nollat10)
ans =
1
>> 2*tosi10
ans =
2 2 2 2 2 2 2 2 2 2
>> 2*tosi10-3.5
ans =
Columns 1 through 7
-1.5000 -1.5000 -1.5000 -1.5000 -1.5000 -1.5000 -1.5000
Columns 8 through 10
-1.5000 -1.5000 -1.5000
|
Huomataan, että totuusarvot ovat myös numeerisia, mutta kääntäen numeeriset funktiot (kuten zeros, ones) tuottavat numeerisen tuloksen, joka ei ole tyyppiä "logical".
Edellistä voidaan hyödyntää usein kätevästi suorittamalla laskutoimituksia totuusarvoilla 0 ja 1, jälkimmäinen on hyvä tiedostaa. Palaamme asiaan find-komennon yhteydessä kohdassa 52.
Merkkijonojen ("string") suhteen kannattaa tässä yhteydessä mainita myös konversiofunktiot num2str ja str2num
>> luvut10
luvut10 =
1 2 3 4 5 6 7 8 9 10
>> ischar(luvut10)
ans =
0
>> merkki10=num2str(luvut10)
merkki10 =
1 2 3 4 5 6 7 8 9 10
>> ischar(merkki10)
ans =
1
>> isnumeric(str2num(merkki10))
ans =
1
>> isequal(str2num(merkki10),luvut10)
ans =
1
>> isequal(str2num(merkki10),merkki10)
ans =
0
>> isequal(merkki10,num2str(luvut10))
ans =
1
|
Jos haluat hassutella merkkijonoilla, niin kokeilepa hyvin vuoksi, mitä antaa >> merkki10+0 . Tälle on luonnollinen (ASCII-) selitys, mutta älä nyt juutu kuitenkaan.
| ja (and) | tai (or) | ei (not) | "joko tai" | tosi, jos kaikki alkiot ~= 0 | tosi, jos jokin alkio ~= 0 |
| & | | | ~ | xor | all | any |
Esimerkki loogisista operaatioista vektoreilla
>> x=[-2,1,0,5];
>> y=[-2,-1,0,1];
>> (x>0) | (y>0)
ans =
0 1 0 1
>> (x>0) & (y>0)
ans =
0 0 0 1
|
Esimerkki all- ja any- funktioista matriiseilla
>> A=reshape(1:6,3,2)'
A =
1 2 3
4 5 6
>> B=A; B(2,2)=-B(2,2)
B =
1 2 3
4 -5 6
>> all(A==B) % all-funktiota sovelletaan sarakkeittain,
ans = % identtiset sarakkeet antavat 1:n (ja vain ne).
1 0 1
>> all(all(A==B)) % Näin voidaan testata, ovatko matriisien kaikki
ans = % alkiot samat.
0
>> any(A==B) % any-funktiota sovelletaan sarakkeittain.
ans = % Jos vastinsarakkeissa on jotkin samat
1 1 1 % vastinalkiot, saadaan 1, muuten 0.
>> any(any(A==B)) % Onko edes yksi vastinalkiopari sama?
ans = % Tässä tapauksessa on (monikin).
1
>> all(any(A==B)) % Onko jokaisessa vastinsarakkeessa ainakin yksi
ans = % sama vastinalkiopari?
1
|
Tällaisia yhdistelmiä voidaan soveltaa luovasti.
Huomaamme (jos olemme lukeneet pitemmälle), että all ja any ovat skalaarifunktioita
Esimerkiksi integraalimuunnosten yhteydessä tarvitaan usein paloittain määritellyn funktion esitystä karakterististen funktioiden (Heavisiden funktioiden) lineaarikombinaationa.
Matlabissa välin karakteristinen funktio voidaan esittää ällistyttävän
näppärästi ja vähäeleisesti.
Ajatellaan, että x on diskretoitu x-akseli
(tietysti käytännössä äärellinen osa sitä) ja a ja b skalaareja. Matlab-lauseke
>> (x > a) & (x < b)antaa x:n pituisen vektorin, joka käyttäytyy halutulla tavalla.
Esimerkki
a=0;b=1; x=linspace(a,b,20) % Karkea diskretointi havainnollistuksen vuoksi. y=(x>a) & (x < b) plot(x,y); % Yhdistetään vektorien x ja y vastinpisteet jananpätkillä. axis([-1,2,-0.1,1.1]);grid;shg % Parannellaan kuvan ulkoasua. |
Jos haluaisimme tarkemman kuvan, voisimme ottaa hienomman diskretoinnin. Tässä tapauksessa olisi toki piirtämisen kannalta ekonomisinta valita 6 pistettä älykkäästi, kuvaajahan koostuu viidestä jananpätkästä.
Erityisesti, jos H on Heavsiden funktio (ts. positiivisen reaaliakselin karakteristinen funktio), niin siirretty funktio H(x-a) saadaan Matlab-lausekkeella >> x > a .
Huomaamme, kuinka kätevää on, että totuusarvoilla 0 ja 1 voi suorittaa myös tavallisia aritmeettisia laskutoimituksia.
Esimerkki
>> rand('state',0) % Kokeen toistettavuuden takia alustus.
>> v=floor(10*rand(1,8)) % Satunnaisia kokonaislukuja välillä [0,10].
v =
9 2 6 4 8 7 4 0
>> indvek=[1 1 3 4 2 2 6 1 7 5 5 5]; % indeksivektori saa olla miten
% pitk„ tahansa, toistoja saa esiintyä
>> v(indvek)
ans =
9 9 6 4 2 2 7 9 4 8 8 8
|
Usein on tarvetta valita vektorista alkiot, jotka toteuttavat tietyt ehdot. Voimme esimerkiksi tarvita kaikki alkiot, jotka ylittävät jonkin kynnysarvon. (Pankinjohtaja voi haluta valita avainasiakkaikseen kaikki ne, joiden pankkitalletusten vuoden keskiarvo ylittää 50 000 mk.)
Funktio find palauttaa nollasta poikkeavien vektorin alkioiden indeksit. Ehtovektoreitahan osaamme muodostaa loogisilla ja järjestysoperaatioilla.
Esimerkki
>> x=[0,1,-3,5,0];
>> ind=find(x)
ind =
2 3 4
>> x(ind)
ans =
1 -3 5
>> x=[x,2*x,-x] % Rakennetaan pitempi ja luvuiltaan vaihtelevampi vektori
x =
Columns 1 through 12
0 1 -3 5 0 0 2 -6 10 0 0 -1
Columns 13 through 15
3 -5 0
>> ind=find(x>=2)
ind =
4 7 9 13
>> x(ind)
ans =
5 2 10 3
|
Yleensä kirjoitetaan suoraan x(find(x>=2)) , mikä on helppo omaksua idiomina.
Matlab sallii myös find-funktion poisjättämisen yllä: x(x>=2)
toimii yhtä hyvin.
Jos ajattelemme tätä idiomina, se on sinänsä
luonteva (ja pankinjohtajankin helposti omaksuttavissa). Sensijaan indeksoinnin
kannalta ajateltuna siinä on näennäinen ristiriita: edellähän olemme oppineet,
että 0 ei kelpaa indeksiksi.
Indeksointiin lisätäänkin nyt sellainen sääntö, että indeksointi loogisella vektorilla toimii niin, että valitaan ykkösiä vastaavat vektorin alkiot ja jätetään nollia vastaavat valitsematta. Varjopuolena on, että looginen ja numeerinen (0/1)-vektori (sanomme lyhyesti: "bittivektori") näyttää samalta, mutta edellinen toimii, kun taas jälkimmäinen johtaa virheeseen.
Suositus
Suosittelemme aina käytettäväksi find-funktiota ehtovalintatilanteissa. Se on yhtä find-sanaa (ja kahta sulkua) pitempi, mutta johdonmukaisempi.
Tehtävä Valitse annetusta vektorista parittomia (vastaavasti parillisia) indeksejä vastaavat alkiot.
Ratkaisu
Eleganttia on käyttää jakojäännosfunktiota rem
v=... % Jokin vektori indeksit=1:length(v) % v:n indeksivektori v(find(rem(indeksit,2)==0)) % Parillisia vastaavat v(find(rem(indeksit,2)~=0)) % Parittomia vastaavat
Funktio find on valmiiksi ohjelmoitu niin, että kutsu ind=find(A) tekee tuon jonoutuksen. (Ei siis tarvitse kirjoittaa: ind=find(A(:)) .) Kaiken lisäksi matriisit ymmärtävät myös jonoutetun indeksin käytön, ts. jos matriisille annetaan indeksivektori, se tulkitsee sen luvut jonoutetun matriisin indekseiksi.
Toisaalta funktiota voidaan myös kutsua : [i,j]=find(A) Tällöin palautetaan indeksivektorit ijaj, jotka rinnakkain asetettuna antavat 0:sta poikkeavien A:n alkioiden paikat. Tämä muoto on erityisen hyödyllinen käsiteltäessä matriiseja "harvoina" ("sparse").
Esimerkki
A=magic(4) % Olkoon A 4 x 4- "taikaneliö"
ehtomat=mod(A,3)==0 % Mitkä alkiot ovat jaollisia 3:lla ?
ind=find(ehtomat) % Indeksit ovat vektoriksi jonoutetun A:n indeksejä.
% (siis sama kuin find(ans(:))
A(ind) %
A(ind)=33 % Sijoitetaan kuhunkin arvo 33.
|
Olkoon A vaikkapa edellinen 4 x 4-taikaneliö (tai mikä tahansa matriisi). Kirjoita Matlab-lauseke, joka korvaa 0:lla kaikki ne A:n luvut, jotka eivät ole jaollisia 3:lla.
Ratkaisu
A=magic(4) % tms. A(find(mod(A,3)~=0))=0
Toisaalta ohjausrakenteiden välttelyssä ei kannata mennä liiallisuuksiin, eikä se aina ole mahdollistakaan.
if lauseke
komentoja
end
Tässä lauseke on skalaari tai yleisemmin matriisi, joka
tyypillisesti saadaan järjestys- tai loogisilla operaatioilla. Komennot
suoritetaan, jos lausekematriisin kaikki alkiot (tarkemmin niiden reaaliosat)
ovat nollasta poikkevia.
Tyypillisimmin lauseke on skalaari.
Yleisesti if -lauseessa voi olla elseif ja else- haaroja. (elseif on kirjoitettava yhteen.)
Koodi voidaan kirjoittaa samalle riville, silloin rivinvaihdot on korvattava
pilkuilla. Selkeyden takia on syytä suosia yllä olevaa kirjoitustapaa
sisennyksineen.
Luonnollisesti ohjausrakenteet kirjoitetaan yleensä
m-tiedostoon, vain aivan yksinkertaisissa tapauksissa kannattaa kirjoittaa
suoraan komentoikkunaan.
Esimerkki
Kirjoitetaan koodi, joka palauttaa arvon 0, jos luku on 0, arvon 1, jos se on positiivinen tai Inf, arvon -1, jos negatiivinen tai -Inf ja virheilmoituksen, jos "luku" on kompleksinen tai NaN.
Vaikka tällainen rakenne voidaan kirjoittaa suoraan Matlab-istuntoon, se ei ole mitenkään järkevää. Kirjoitamme koodin tiedostoon ifesim.m . Laitamme alkuun input-lauseen, joka kysyy käyttäjältä syötelukua n.
n=input('Anna luku tai +-Inf ')
' Jos annoit kompleksiluvun tai NaN:n, syytä itseäsi. '
if imag(n)~=0
error('Haluan reaaliluvun')
elseif n < 0
tulos=-1
elseif n==0
tulos=0
elseif n > 0
tulos=1
else
error('Haluan reaaliluvun, tai +/- Inf:n, NaN ei käy. ')
end
|
Switch-esimerkki
Kirjoitetaan muunnelma edellisestä, joka sopii switch-rakenteelle. Tehdään se tiedostoon switchesim.m .
n=input('Anna luku tai +-Inf ')
switch n
case 0
'Annoit luvun 0'
case 1
'Annoit luvun 1'
case -1
'Annoit luvun -1'
otherwise
['Annoit jotain muuta, tarkemmin sanottuna ',num2str(n),':n']
end
|
Switch-rakenne soveltuu siis tilanteeseen, jossa haaraudutaan muutaman "vaihdemuuttujan" arvon mukaan. Toisin kuin if-lauseessa, tässä ei käytetä loogisia ehtoja, vaan rakenne itsessään sisältää "vaihdemuuttujan" vertailun "tapausarvoon".
Näyttää siltä, että kompleksinen vaihdemuuttuja toimii jonkin tämän kirjoittajalle vaikeasti aukeavan logiikan mukaisesti. En voi nyt muuta kuin suositella pitäytymistä reaalisissa (tai käyttämään if-rakennetta).
Yllä oleva koodi toimii järkevästi reaaliluvuilla sekä syötteillä Inf,-Inf, NaN ja 'kissa'. Kompleksilukujen suhteen se puhuu joskus palturia.
for muuttuja=vektorilauseke komennot endMuuttuja käy läpi kaikki vektorilausekkeen komponentit ja suorittaa kullakin komennot. Useimmiten vektorilauske on muotoa 1:n tai alku:askel:loppu. Mikään ei estä käyttämästä vaikkapa vektoria
Esimerkki (tyhmä)
Lasketaan vektorin alkioiden itseisarvojen summa "vääräoppisella" tavalla.
v=... % Annetaan vektori v n=length(v); summa=0; for k=1:n summa=summa+abs(v(k)); end; |
Esimerkki (viisaampi)
Iteroidaan neliöjuurifunktiota annettuun lähtäarvoon ja talletetaan koko iteraatiojono vektoriksi iterjono .
a=5 % Annetaan iteraation lähtäarvo, olkoon 5 n=10 % Iteraatiokierrosten lukumäärä %%%%%%%%%%% iter.m alkaa %%%%%%%%%%%%%%%%%% iterjono=[]; % Alustetaan iterjono tyhjäksi vektoriksi. uusiarvo=a; for k=1:n iterjono=[iterjono,uusiarvo]; uusiarvo=sqrt(uusiarvo); end; iterjono %%%%%%%%%%%%%% iter.m loppuu %%%%%%%%%%%% |
Jos kirjoitamme yllä merkityn osan tiedostoon iter.m, voimme edetä Matlab-istunnossamme seuraavaan tapaan:
a=5;n=10;
iter % Suoritetaan tiedostossa iter.m olevat komennot.
a=iterjono(end) % Uudeksi alkuarvoksi viimeinen edellä saatu arvo
a =
1.0031
>> iter % Suoritetaan tiedostossa iter.m olevat komennot,
iterjono = % alkuarvona on edellisen iteroinnin viimeinen arvo.
Columns 1 through 7
1.0031 1.0016 1.0008 1.0004 1.0002 1.0001 1.0000
Columns 8 through 10
1.0000 1.0000 1.0000
>> format long % Täysi tulostustarkkuus
>> iter % Nyt ei muuteta alkuarvoa, katsotaan edellistä tarkemmin
iterjono =
Columns 1 through 4
1.00314837919044 1.00157295250543 1.00078616722326 1.00039300638462
Columns 5 through 8
1.00019648388935 1.00009823711941 1.00004911735345 1.00002455837517
Columns 9 through 10
1.00001227911220 1.00000613953725
>> format short % Palataan oletustulostustarkkuuteen.
|
Esimerkki sisäkkäisistä silmukoista, Hilbertin matriisi
Muodostetaan ns. Hilbertin matriisi, jonka alkiot ovat H(i,j)=1/(i+j-1).
m=4;n=4 % Annetaan m ja n
for i=1:m
for j=1:n
H(i,j)=1/(i+j-1);
end
end
H % Näytä tulos.
H =
1.0000 0.5000 0.3333 0.2500
0.5000 0.3333 0.2500 0.2000
0.3333 0.2500 0.2000 0.1667
0.2500 0.2000 0.1667 0.1429
|
Tässä on esimerkki tilantessa, joka on varmasti helpointa kirjoittaa alkiotason silmukointina. Matriisioperaatioratkaisu vaatii hieman kokemusta. Itse asiassa Matlabissa on valmis funktio hilb, jonka on kirjoittanut Matlab:n luoja, Cleve Moler. Koodin voi katsoa komennolla type hilb .
while lauseke
komennot
end
Komennot suoritetaan niin kauan kuin lauseke on tosi.
While-rakenne on sopivampi iterointiin kuin for sikäli, että lopetusehto voidaan ottaa luontevasti mukaan.
Esimerkki, kone-epsilon
Kone-epsilon on suurin liukuluku eps>0, joka lisättynä 1:een antaa tulokseksi 1. Kyseessä on liukulukujärjestelmän suhteellisen tarkuuden mitta, jota myös pyöristysyksiköksi sanotaan.
e=1; % Alustus while 1+e > 1 e=e/2; end e eps % Systeemimuuttuja eps antaa arvion kone-epsilonille abs(e-eps) % Paljonko eroavat |
Tämä koodi voi antaa "pahimmassa tapauksessa" arvon eps/2 riippuen alkuarvosta. Kone-epsilonin tapauksessa tärkeää on tietää suuruusluokka, kertoimella 2 ei ole merkitystä.
Siis jos f on skalaarifunktio, niin
f(skalaari) -> skaalaari | f(a1 1) ... f(a1 n) | | f(a2 1) ... f(a2 n) | f(A) -> | ... | | ... | | f(am 1) ... f(am n) |
Otetaanpa hieman laajempi luettelo Matlabin skaalaarifunktioita:
sin asin exp abs round
cos acos log sqrt floor
tan atan rem sign ceil
Jos joku näistä on tuntematon, niin muistathan katsoa helpistä.
Esimerkki, sum, max
A=reshape(1:12,4,3) sum(A) max(A) |
Other MATLAB functions operate essentially on a vector (row or column), but act on an m-by-n matrix (m>=2) in a column-by-column fashion to produce a row vector containing the results of their application to each column. Row-by-row action can be obtained by using the transpose; for example, mean(A')'.
f(vekt) -> skal f(A) operoi sarakkeittain: | | | | | f(a. 1) ... f(a. n) | f(A) -> | | | | | | | |A few of these functions are
max sum median any floor min prod mean all ceil round sort stdFor example, the maximum entry in a matrix A is given by max(max(A)) rather than max(A). Try it.
Matriisin jonoutus pitkäksi sarakevektoriksi saadaan aikaan kirjoittamalla
A(:)Niinpä matriisin A suurin alkio saadaan myös näin: max(A(:)) . Kokeile tätäkin.
Jonoutetusta pitkästä vektorista päästään takaisin matriisiin komennolla reshape , joka on varsin kätevä moneen hommaan, katso helpwin reshape .
Tehtävä: (a) Kirjoita lauseke, joka laskee matriisin A alkioiden
itseisarvojen sarakesummien maksimin.
(b) Sama rivisummille.
Edellinen
on matriisin ns. 1-normi, jälkimmäinen taas "ääretön-normi", näistä enemmän
tuonnempana.
eig, inv, svd, lu, rref, expm, det, size, norm, cond, rankLukijaa kehoitetaan tutkimaan näitä helpin avulla.
Mainittakoon tässä eig .
lam=eig(A)
antaa neliömatriisin ominaisarvot.
Kutsulla
[V,D]=eig(A)saadaan diagonaalimatriisi D, jonka diagonaalilla ovat ominaisarvot, ja vastaavista ominaisvektorisarakkeista koostuva matriisi V.
Tehtävä: Muodosta symmetrinen 10 x 10 satunnaismariisi (käyttäen rand -funktiota), nimeltään A. Huomaa, että symmetrisen matriisin saat esim. kertomalla mielivaltaisen matriisin ja sen transpoosin keskenään. Muodosta matriisit V ja D, missä V:n sarakkeet ovat A:n ominaisvektorit ja D:n diagonaalialkiot ovat A:n ominaisarvot. Laske A*V ja V*D ja totea ne samoiksi. Muistele ominaisarvojen ja - vektoreiden määritelmää ja perustele, miksi näin on.
Ympäristö on Unix:n tcshell-komentotilan tyylinen:
Matlab-ikkunassa voidaan pystyttää pikaisesti ihan merkittäviä on-line algoritmeja suorittamalla iteraatiota nuolinäppäimellä. Tarvittaessa kannattaa venyttää Matlab-ikkuna leveäksi, jotta saadaan pitkä (tarvittaessa pari pitkää riviä) algoritmin ytimeksi. Tätä toimintaa kannattaa suunnitella yhdessä editori-ikkunan kanssa (muista myös kynä ja paperi!)
Esim: Ratkaise f(x)=0 Newtonin menetelmällä , kun f(x)=x*exp(-x)-sin(5*x) Verrataan vielä kuvaan zoomaamalla.
x=linspace(0,5);y=x.*exp(-x)-sin(5*x);plot(x,y);grid;shg
Lasketaan derivaatta Maplella:
|\^/| Maple V Release 5.1 (Helsinki University of Technology)
._|\| |/|_. Copyright (c) 1981-1998 by Waterloo Maple Inc. All rights
\ MAPLE / reserved. Maple and Maple V are registered trademarks of
<____ ____> Waterloo Maple Inc.
| Type ? for help.
> diff(x*exp(-x)-sin(5*x),x);
exp(-x) - x exp(-x) - 5 cos(5 x)
%Valitaan kuvasta alkupiste 1.3.
x=1.3;
fx=x.*exp(-x)-sin(5*x);dfx=exp(-x)-x.*exp(-x)-5*cos(5*x);x=x-fx./dfx
1+x2-y2+excos y = 0 2 x y + ex sin y = 0Piirretään ensin:
clf x=linspace(-2,5,40);y=linspace(-6,6,40); [X,Y]=meshgrid(x,y); Z1=1+X.^2-Y.^2+exp(X).*cos(Y); Z2=2*X.*Y+exp(X).*sin(Y); contour(X,Y,Z1,[0 0]) hold on contour(X,Y,Z2,[0 0],'r') shg figure surfl(X,Y,Z1);hold on; surfc(X,Y,Z2);colorbar;shg;grid
%%%%%%% funjac.m %%%%%%%%%%%%
function [f,J]=funjac(x)
% Kutsuesim: [f,J]=funjac([1,2]) % Lasketaan funktio ja Jakobiaani pist [1,2].
% Tämä on algoritmin ongelmariippuva osa, käytä tarvittaessa Maplea
% Jakobiaanin muodostamiseen
function [f,J]=funjac(x)
% Kutsuesim: [f,J]=funjac([1,2]) % Lasketaan funktio ja Jakobiaani pist [1,2].
% Tämä on algoritmin ongelmariippuva osa, käytä tarvittaessa Maplea
% Jakobiaanin muodostamiseen
f=[1+x(1)^2-x(2)^2+exp(x(1))*cos(x(2)); 2*x(1)*x(2)+exp(x(1))*sin(x(2))];
J=[2*x(1) + exp(x(1))*cos(x(2)), -2*x(2) - exp(x(1))*sin(x(2))
2*x(2) + exp(x(1))*sin(x(2)), 2*x(1) + exp(x(1))*cos(x(2))];
%%%%%%%%% end funjac.m %%%%%%%%%%%%%%%%%%%%%%%%%
\ MAPLE / reserved. Maple and Maple V are registered trademarks of
<____ ____> Waterloo Maple Inc.
| Type ? for help.
> with(linalg):
> jacobian([1+x^2-y^2+exp(x)*cos(y),2*x*y+exp(x)*sin(y)],[x,y]);
[2 x + exp(x) cos(y) -2 y - exp(x) sin(y)]
[ ]
[2 y + exp(x) sin(y) 2 x + exp(x) cos(y) ]
Sitten iteroidaan: x=[1;-2]; [fx,Jx]=funjac(x);h=-Jx\fx;x=x+h Tai vaikka: x=ginput x=x' [fx,Jx]=funjac(x);h=-Jx\fx;x=x+h
format compact
f=inline('t.^2-y','t','y')
clf;hold on, grid, title('dy/dt=t^2-y'); n=2;a=0;b=4;ya=1;
[T,Y]=euleri(f,a,b,ya,n);plot(T,Y,T,Y,'o'); shg;[T',Y'], n=2*n
%%%%%% euleri.m %%%%%%%%%%%%
function [T,Y]=euleri(f,a,b,ya,n)
h=(b-a)/n;
Y=zeros(1,n+1);T=Y;
T(1)=a;Y(1)=ya;
for j=1:n
Y(j+1)=Y(j)+h*feval(f,T(j),Y(j));
T(j+1)=a+j*h;
end;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
a:b % vektori: [a,a+1,...,b] a:h:b % vektori: [a,a+h,...,b]Viimeinen alkio voi jäädä b:tä vähän pienemmäksi, jos jako "ei mene tasan", mutta se on harvemmin tärkeää. Kts. myös help colon .
Kokeile esim:
>> -5:6 >> -3.1:0.1:4 >> 2:-0.5:-1Kaksoispiste antaa kätevän tavan muodostaa tasavälisesti diskretoitu x-vektori, kun askelpituus on annettu. Tämä on hyödyllinen piirtämisessä ja taulukoinnissa:
>> x=-pi:0.1:pi; y=sin(x); >> plot(x,y) >> [x' y']Jos haluamme antaa jakopisteiden lukumäärän, voimme käyttää valmista linspace -funktiota. Mikään ei estäisi rakentamasta sitä myöskään tähän tapaan:
>> a=-pi; b=pi; n=20; % Muuteltavat arvot. >> h=(b-a)/n; >> x=a:h:b;(Pieni ero syntyy loppupisteen käsittelyssä, mutta se ei useimmiten ole kiinnostavaa.)
Vectors and submatrices are often used in MATLAB to achieve fairly complex data manipulation effects. Colon notation" (which is used both to generate vectors and reference submatrices) and subscripting by vectors are keys to efficient manipulation of these objects. Creative use of these features permits one to minimize the use of loops (which slows MATLAB) and to make code simple and readable. Special effort should be made to become familiar with them.
The expression 1:5 (met earlier in for statements) is actually the row vector [1 2 3 4 5]. The numbers need not be integers nor the increment one. For example,
0.2:0.2:1.2gives [0.2, 0.4, 0.6, 0.8, 1.0, 1.2], and
5:-1:1 gives [5 4 3 2 1].The following statements will, for example, generate a table of sines. Try it.
x = [0.0:0.1:2.0]' ; y = sin(x); [x y]Note that since sin operates entry-wise, it produces a vector y from the vector x.
The colon notation can be used to access submatrices of a matrix. For example,
A(1:4,3) is the column vector consisting of the first four entries of the third column of A.A colon by itself denotes an entire row or column:
A(:,3) is the third column of A , and A(1:4,:) is the first four rows.Arbitrary integral vectors can be used as subscripts:
A(:,[2 4]) contains as columns, columns 2 and 4 of A .Such subscripting can be used on both sides of an assignment statement:
A(:,[2 4 5]) = B(:,1:3) replaces columns 2,4,5 of A with the first three columns of B. Note that the entire altered matrix A is printed and assigned. Try it.Columns 2 and 4 of A can be multiplied on the right by the 2-by-2 matrix [1 2;3 4]:
A(:,[2,4]) = A(:,[2,4])*[1 2;3 4]Once again, the entire altered matrix is printed and assigned.
If x is an n-vector, what is the effect of the statement x = x(n:-1:1)? Try it.
To appreciate the usefulness of these features, compare these MATLAB statements with a Pascal, FORTRAN, or C routine to effect the same.
There are two types of M-files: script files and function files.
Script files. A script file consists of a sequence of normal MATLAB statements. If the file has the filename, say, rotate.m, then the MATLAB command rotate will cause the statements in the file to be executed. Variables in a script file are global and will change the value of variables of the same name in the environment of the current MATLAB session.
Script files are often used to enter data into a large matrix; in such a file, entry errors can be easily edited out. If, for example, one enters in a diskfile data.m
A = [ 1 2 3 4 5 6 7 8 ];then the MATLAB statement data will cause the assignment given in data.m to be carried out.
An M-file can reference other M-files, including referencing itself recursively.
Function files. Function files provide extensibility to MATLAB. You can create new functions specific to your problem which will then have the same status as other MATLAB functions. Variables in a function file are by default local. However, version 4.0 (nyt on jo 5.3) permits a variable to be declared global.
We first illustrate with a simple example of a function file. Otetaan pari vielä yksinkertaisempaa. Määritellään funktio 'sincos', joka laskee sinin ja cosinin tulon.
function y=sincos(x) y=sin(x).*cos(x);Huomaa vektorointi .*-kertolaskulla. (Muuten emme voisi edes piirtää alla olevalla standarditavalla.) Huom! Uusissa Matlabin versioissa tällaiset pikku funktiot voidaan myös määritellä suoraan Matlab-istunnossa:
sincos=inline('sin(x).*cos(x)','x');
Piirretään
x=linspace(0,2*pi); plot(x,sincos(x)); shgSitten kaksi tulosarvoa palauttava pikku esimerkki.
function [mean,stdev] = stat(x)
% Keskeisiä tilastollisia tunnuslukuja
% x - vektori
% esim: [ke,std]=stat(1:10)
n = length(x);
mean = sum(x) / n;
stdev = sqrt(sum((x - mean).^2)/n);
function a = randint(m,n) %RANDINT Randomly generated integral matrix. % randint(m,n) returns an m-by-n such matrix with entries % between 0 and 9. a = floor(10*rand(m,n));A more general version of this function is the following:
function a = randint(m,n,a,b) %RANDINT Randomly generated integral matrix. % randint(m,n) returns an m-by-n such matrix with entries % between 0 and 9. % rand(m,n,a,b) return entries between integers a and b . if nargin < 3, a = 0; b = 9; end a = floor((b-a+1)*rand(m,n)) + a;This should be placed in a diskfile with filename randint.m (corresponding to the function name). The first line declares the function name, input arguments, and output arguments; without this line the file would be a script file. Then a MATLAB statement z = randint(4,5), for example, will cause the numbers 4 and 5 to be passed to the variables a and b in the function file with the output result being passed out to the variable z. Since variables in a function file are local, their names are independent of those in the current MATLAB environment.
Note that use of nargin ("number of input arguments") permits one to set a default value of an omitted input variable-such as a and b in the example.
Tehtävä Kirjoita tämä tiedostoon randint.m (Voit leikata/liimata tästä suoraan, onhan sinulla emacs auki!) (Tietysti UNIX:ssa näinkin: Hiiren vasen, maalaus, cat > randint.m, hiiren keskimmäinen, CTR-D). Kokeile help randint ja testaa.
Kehitetään yllä oleva stat-funktio tomimaan vektorifunktioiden tavoin, jos syötteenä on matriisi, siis saraketyyliin, kuten sum, max jne.
function [mean, stdev] = stat(x) % STAT Mean and standard deviation % For a vector x, stat(x) returns the % mean and standard deviation of x. % For a matrix x, stat(x) returns two row vectors containing, % respectively, the mean and standard deviation of each column. [m n] = size(x); if m == 1 m = n; % handle case of a row vector end mean = sum(x)/m; stdev = sqrt(sum(x.^ 2)/m - mean.^2);Once this is placed in a diskfile stat.m, a MATLAB command [xm, xd] = stat(x), for example, will assign the mean and standard deviation of the entries in the vector x to m and xd, respectively. Single assignments can also be made with a function having multiple output arguments. For example, xm = stat(x) (no brackets needed around xm) will assign the mean of x to xm.
The % symbol indicates that the rest of the line is a comment; MATLAB will ignore the rest of the line. However, the first few comment lines, which document the M-file, are available to the on-line help facility and will be displayed if, for example, help stat is entered. Such documentation should always be included in a function file.
This function illustrates some of the MATLAB features that can be used to produce efficient code. Note, for example, that x.^2 is the matrix of squares of the entries of x, that sum is a vector function (section 8), that sqrt is a scalar function (section 7), and that the division in sum(x)/m is a matrix-scalar operation.
The following function, which gives the greatest common divisor of two integers via the Euclidean algorithm, illustrates the use of an error message (see the next section).
function a = gcd(a,b)
% GCD Greatest common divisor
% gcd(a,b) is the greatest common divisor of
% the integers a and b, not both zero.
a = round(abs(a)); b = round(abs(b));
if a == 0 & b == 0
error('The gcd is not defined when both numbers are zero')
else
while b ~= 0
r = rem(a,b);
a = b; b = r;
end
endSome more advanced features
are illustrated by the following function. As noted earlier, some of the input
arguments of a function-such as tol in the example, may be made
optional through use of nargin ("number of input arguments"). The
variable nargout can be similarly used. Note that the fact that a
relation is a number (1 when true; 0 when false) is used and that, when
while or if evaluates a relation, "nonzero" means "true" and
0 means "false". Finally, the MATLAB function feval permits
one to have as an input variable a string naming another function. function [b, steps] = bisect(fun, x, tol)
%BISECT Zero of a function of one variable via the bisection method.
% bisect(fun,x) returns a zero of the function. fun is a string
% containing the name of a real-valued function of a single
% real variable; ordinarily functions are defined in M-files.
% x is a starting guess. The value returned is near a point
% where fun changes sign. For example,
% bisect('sin',3) is pi. Note the quotes around sin.
%
% An optional third input argument sets a tolerence for the
% relative accuracy of the result. The default is eps.
% An optional second output argument gives a matrix containing a
% trace of the steps; the rows are of form [c f(c)].
% Initialization
if nargin < 3, tol = eps; end
trace = (nargout == 2);
if x ~= 0, dx = x/20; else, dx = 1/20; end
a = x - dx; fa = feval(fun,a);
b = x + dx; fb = feval(fun,b);
% Find change of sign.
while (fa > 0) == (fb > 0)
dx = 2.0*dx;
a = x - dx; fa = feval(fun,a);
if (fa > 0) ~= (fb > 0), break, end
b = x + dx; fb = feval(fun,b);
end
if trace, steps = [a fa; b fb]; end
% Main loop
while abs(b - a) > 2.0*tol*max(abs(b),1.0)
c = a + 0.5*(b - a); fc = feval(fun,c);
if trace, steps = [steps; [c fc]]; end
if (fb > 0) == (fc > 0)
b = c; fb = fc;
else
a = c; fa = fc;
end
endSome of MATLAB's functions
are built-in while others are distributed as M-files. The actual listing of any
M-file-MATLAB's or your own-can be viewed with the MATLAB command type
functionname. Try entering type eig, type vander,
and type rank.
Opettavaista katsoa, miten "isot pojat/tytöt" Mathworks:ssa ovat funktioita kirjoitelleet. Sama pätee Mapleen (Maplesoft).
s = 'This is a test'assigns the given text string to the variable s.
Text strings can be displayed with the function disp. For example:
disp('this message is hereby displayed')Error
messages are best displayed with the function error error('Sorry, the matrix must be symmetric')since
when placed in an M-File, it causes execution to exit the M-file.
In an M-file the user can be prompted to interactively enter input data with the function input. When, for example, the statement
iter = input('Enter the number of iterations: ')is
encountered, the prompt message is displayed and execution pauses while the user
keys in the input data. Upon pressing the return key, the data is assigned to
the variable iter and execution resumes.
The MATLAB function flops keeps a running total of the flops performed. The command flops(0) (not flops = 0!) will reset flops to 0. Hence, entering flops(0) immediately before executing an algorithm and flops immediately after gives the flop count for the algorithm.
tic ja toc, esim:
A=rand(100,100);b=ones(100,1); tic; x = A \ b; toc
format short fixed point with 4 decimal places (the default) format long fixed point with 14 decimal places format short e scientific notation with 4 decimal places format long e scientific notation with 15 decimal placesOnce invoked, the chosen format remains in effect until changed.
The command format compact will suppress most blank lines allowing more information to be placed on the screen or page. It is independent of the other format commands.
MATLAB can produce both planar plots and 3-D mesh surface plots. To preview some of these capabilities in version 3.5, enter the command plotdemo.
Planar plots. The plot command creates linear x-y plots; if x and y are vectors of the same length, the command plot(x,y) opens a graphics window and draws an x-y plot of the elements of x versus the elements of y. You can, for example, draw the graph of the sine function over the interval -4 to 4 with the following commands:
x = -4:.01:4; y = sin(x); plot(x,y)Try it. The vector x is a partition of the domain with meshsize 0.01 while y is a vector giving the values of sine at the nodes of this partition (recall that sin operates entrywise).
Kuten edellä oli puhe, usein linspace voi olla kätevämpikin (saadaan aina 100:aan osaan jako, jos käytetään oletusarvoa). Siis edellä olisi yhtä hyvin voitu kirjoittaa:
x=linspace(-4,4);plot-funktion toiminnasta saa havainnollisen kuvan ottamalla harvan diskretoinnin. Kokeile vaikka näin:
x=linspace(-4,4,10); y=sin(x); [x' y'], plot(x,y)Varmista, että ymmärrät kaiken, kiinnitä myös huomiota puolipisteisiin ja pilkkuun, tässä on kaikki harkittua. Huomaa, että Matlabin nuolinäppäineditointityylillä on kätevää operoida, kun kirjoitetaan pitkiä rivejä. Tässäkin tarvitaan vain yksi nuolipainallus, jonka jälkeen voidaan esim. diskretointimäärää käydä muuttamassa ja lähettää rivi uudelleen suoritukseen.
Tehtävä Piirrä funktion
As a second example, you can draw the graph of y=e-x^2 over the interval -1.5 to 1.5 as follows:
x = -1.5:.01:1.5; y = exp(-x.^2); plot(x,y)Note that one must precede the power-to sign by a period to ensure that it operates entrywise (see section 3).
Parametrimuodossa annetut käyrät
Plots of parametrically defined curves can also be made. Try, for example,
t=0:.001:2*pi; x=cos(3*t); y=sin(2*t); plot(x,y)Ennen tätä kannattaa kokeilla kaikkein perustavanlaatuisinta, eli yksikköympyrää (piirrämme oikeastaan 100-kulmion):
t=linspace(0,2*pi);x=cos(t);y=sin(t);plot(x,y);
axis('equal');axis('square')Vertaa tätä kuvaan t=linspace(0,2*pi);x=cos(t);y=sin(t);plot(t,x,'r',t,y,'b');Ymmärräthän nyt varmasti! Vrt. Maplen parametripiirto, harj0.mws , [HAM] s. 93
The command grid will place grid lines on the current graph. Kannattaa käyttää !
Jos ympyrä on perusparametrikäyrä tasossa, niin ruuviviiva on sitä avarudessa.
t=linspace(0,4*pi);x=cox(t);y=sin(t);z=t; plot3(x,y,z); % RuuviviivaNapakoordinaatistossa annettu käyrä
fii=linspace(fii1,fii2);x=r(fii).*cos(fii);y=r(fii).*sin(fii);
plot(x,y);
axis('equal');axis('square');grid % Usein näissä halutaan sama
% skaala akseleilleM
atlabissa on myös funktio polar , jossa napakoordinaattimuunnos on
sisäänrakennettu. Sitä käyttäen voidaan piirtää suoraan näin: fii=linspace(fii1,fii2);polar(fii,r(fii)); grid % Lisäbonuksena saadaan myös hilaviivat napakoordinaattiviivoinaLisää napakoordinaattiesim. [BB] s. 53 -> ja sec 10.3 ja exe 10.1, 10.3 The graphs can be given titles, axes labeled, and text placed within the graph with the following commands which take a string as an argument.
title graph title xlabel x-axis label ylabel y-axis label gtext interactively-positioned text text position text at specified coordinatesFor example, the command
title('Best Least Squares Fit')gives
a graph a title. The command gtext('The Spot') allows a mouse or the
arrow keys to position a crosshair on the graph, at which the text will be
placed when any key is pressed. Tämäkin voidaan nykyisin hoitaa kuvaikkunan
valikosta.
By default, the axes are auto-scaled. This can be overridden by the command axis. If c=[xmin,xmax,ymin,ymax] is a 4-element vector, then axis(c) sets the axis scaling to the precribed limits. By itself, axis freezes the current scaling for subsequent graphs; entering axis again returns to auto-scaling. The command axis('square') ensures that the same scale is used on both axes. In version 4.0, axis has been significantly changed; see help axis.
Two ways to make multiple plots on a single graph are illustrated by
x=0:.01:2*pi;y1=sin(x);y2=sin(2*x); y3=sin(4*x);plot(x,y1,x,y2,x,y3)and by forming a matrix Y containing the functional values as columns
x=0:.01:2*pi; Y=[sin(x)', sin(2*x)', sin(4*x)']; plot(x,Y)Another way is with hold. The command hold freezes the current graphics screen so that subsequent plots are superimposed on it. Entering hold again releases the "hold." The commands hold on and hold off are also available in version 4.0.
One can override the default linetypes and pointtypes. For example,
x=0:.01:2*pi; y1=sin(x); y2=sin(2*x); y3=sin(4*x); plot(x,y1,'--',x,y2,':',x,y3,'+') plot(x,y1,'--b',x,y2,'g',x,y3,'+y')renders a dashed line and dotted line for the first two graphs while for the third the symbol is placed at each node. The line- and mark-types are
Linetypes: solid (-), dashed (-). dotted (:), dashdot (-.)See help plot for line and mark colors.Marktypes: point (.), plus (+), star (*), circle (o), x-mark (x)
Viimeisellä rivillä lisättiin vielä värimääreet (lisää help plot, help color).
'b' - blue, 'g' - green, 'y' - yellowThe command subplot can be used to partition the screen so that up to four plots can be viewed simultaneously. See help subplot.
Kuva voidaan myös tulostaa tiedostoon monissa eri muodoissa, kuten eps, gif, jpeg, ym. Voidaan käyttää print-komennon valitsimia tai tulostaa suoraan grafiikkaikkunan valikosta. Versiossa 5.3 on mahdollisuus myös editoida kuvaa piirtämällä siihen viivoja, lisäämällä tekstiä ym. Valikko selittää itse itsensä.
Piirtoikkunat, figure, clf, shg
Grafiikkakomento (kuten plot) avaa ikkunan numero 1. Jos halutaan ohjata grafiikka uuteen ikkunaan, komennetaan figure tai figure(n). Aiemmin avattuihin ikkunoihin päästään käsiksi komenttamalla vaikkapa figure(1) , jolloin voidaan jatkaa piirtämistä ensimmäiseen ikkunaan, arvatenkin käytteän hyväksi hold on komentoa, tai voidaan editoida kuvaa, tulostaa se, ym.
3-D mesh plots. Three dimensional mesh surface plots are drawn with the function mesh. The command mesh(z) creates a three-dimensional perspective plot of the elements of the matrix z. The mesh surface is defined by the z-coordinates of points above a rectangular grid in the x-y plane. Try mesh(eye(10)).
To draw the graph of a function z=f(x,y) over a rectangle, one first defines vectors x and y which give partitions of the sides of the rectangle. With the function meshgrid one then creates a matrix X, each row of which equals x and whose column length is the length of y, and similarly a matrix Y, each column of which equals y, as follows:
[X,Y] = meshgrid(x,y);One then computes a matrix Z, obtained by evaluating f entrywise over the matrices X and Y, to which mesh can be applied.
You can, for example, draw the graph of z=e-x^2-y^2 over the square [-2,2] x [-2,2] as follows (try it):
x = -2:.1:2; y = x; [X,Y] = meshgrid(x,y); Z = exp(-X.^2 - Y.^2); mesh(x,y,Z) % yhtä hyvin mesh(X,Y,Z)You are referred to the User's Guide for further details regarding mesh.
Lisää [BB] s. 54 ->
Kts. myös surf, surfc, contour, waterfall, etc.In version 4.0, the 3-D graphics capabilities of MATLAB have been considerably expanded. Consult the on-line help for plot3, mesh, and surf.
Katselusuuntaa voi säädellä view-komennolla ja versiossa 5.3 voi kuvaa pyöritellä myös grafiikkaikkunan valikosta hiiren avulla. (Ei ihan niin hienosti kuin Maplessa mutta toisaalta grafiikka on Matlabissa paljon nopeampaa.)
Jatketaan vielä yllä olevaa esimerkkiä piirtämällä vierekkäin pintakuva ja korkeuskäyrät, lisätään tekstejä:
subplot(1,2,1),surfc(x,y,Z)
title('Pintapiirros')
subplot(1,2,2),contour(x,y,Z)
title('Korkeuskäyrät')
x=linspace(a,b);plot(x,f(x))Hieman vaivattomammin voimme tehdä näin
fplot('f',[a,b])Tämä vastaa läheisemmin sitä tapaa, jota
esim. Maplen plot noudattaa. (Käyttäjän ei tarvitse huolehtia diskretoinnista.)
Kokeile nyt aluksi vaikka fplot('log',[0.5,2])
Tehtävä Piirrä fplot:n avulla
funktion
A={'Otsikko';[1 2;3 4];magic(10)}
A
celldisp(A)
cellplot(A)
A{1,1},A{2,1},A{3,1}
%% ei toimi näin: %[ots,ykakone,taika10]=deal([A{1,1},A{2,1},A{3,1}])
A={'Otsikko';{1 2;3 4};magic(10)}
A
celldisp(A)
cellplot(A)
clear
AA={'A';magic(3)}
nimi=AA{1}
A=AA{2}
clear
M=magic(4)
A.nimi='M'
A.data=M
A2.nimi='A2'
A2.data=A.data^2
for i=1:5
nimet{i}=['nimi',num2str(i)]
end;
cellplot(nimet);shg
A(:,:,1)=[1 2 3;-2 3 -1;5 -4 -1];A(:,:,2)=vander(1:3);
A(:,:,1) =
1 2 3
-2 3 -1
5 -4 -1
A(:,:,2) =
1 1 1
4 2 1
9 3 1
» max(A)
ans(:,:,1) =
5 3 3
ans(:,:,2) =
9 3 1
» min(A)
ans(:,:,1) =
-2 -4 -1
ans(:,:,2) =
1 1 1
» whos
Name Size Bytes Class
A 3x3x2 144 double array % 3 riviä, 3 saraketta, 2 tasoa
ans 1x3x2 48 double array
min(min(A))
ans(:,:,1) =
-4
ans(:,:,2) =
1
» min(min(min(A)))
ans =
-4
» min(A(:))
ans =
-4
A
sum(A)
A(:,:,1) =
1 2 3
-2 3 -1
5 -4 -1
A(:,:,2) =
1 1 1
4 2 1
9 3 1
ans(:,:,1) =
4 1 1 % 1. tason sarakesummat
ans(:,:,2) =
14 6 3 % 2. tason sarakesummat
cumsum(A)
ans(:,:,1) =
1 2 3 % 1. tason sarakkeittain otetut kumulatiiviset summat
-1 5 2
4 1 1
ans(:,:,2) =
1 1 1 % 2. tason sarakkeittain otetut kumulatiiviset summat
5 3 2
14 6 3
Vastaavasti: prod, cumprod
format compact x=[1 1 3 4 5 1 9 8] [m,y]=hist(x,10) % Oletusarvo 10, toimii siten muodossa hist(x). bar(y,m)
Aika havainnollinen esim. talosta, jossa 3 kerrosta, ... s. 437-8.
house=ceil(10*rand(3,3,3,4))
A=cell(3,4)
for i=1:3
for j=1:4
A{i,j}=ceil(10*rand(3,3));
end;
end;
celldisp(A)
cellplot(A)
>> help colspace
--- help for sym/colspace.m ---
COLSPACE Basis for column space.
The columns of B = COLSPACE(A) form a basis for the column space of A.
SIZE(B,2) is the rank of A.
Example:
colspace(sym(magic(4))) is
[ 0, 1, 0]
[ 0, 0, 1]
[ 1, 0, 0]
[ -3, 1, 3]
See also NULL.
There are many functions beyond these. There exist, in particular, several "toolboxes" of functions for specific areas; included among such are signal processing, control systems, robust-control, system identification, optimization, splines, chemometrics, mu-analysis and synthesis, state-space identification, and neural networks. (The toolboxes, which are optional, may not be installed on your system.) These can be explored via the command help.
General