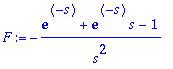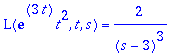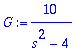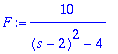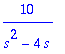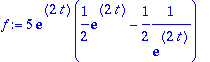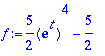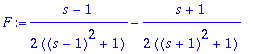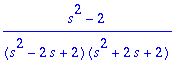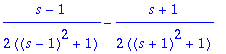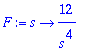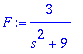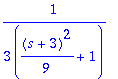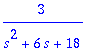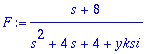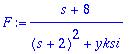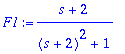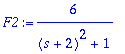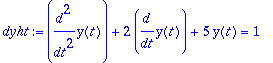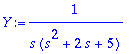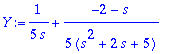1.
a)
| > | restart:with(inttrans):alias(L=laplace,IL=invlaplace): # Jätetään u vapaaksi. |
Warning, the name changecoords has been redefined
| > | f:=t^2; |
![]()
| > | FT:=Int(f*exp(-s*t),t=0..T); |
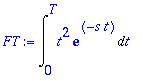
| > | u:=t^2; dv:=exp(-s*t); v:=int(dv,t); du:=diff(u,t); |
![]()
![]()
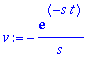
![]()
| > | FT:=subs(t=T,u*v)-subs(t=0,u*v)-Int(v*du,t=0..T); |
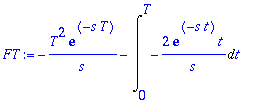
1. termi menee o:aan, kun T lähenee
![]() :tä.
:tä.
Laskettavaksi jää:
| > | FT:=Int(2*exp(-s*t)/s*t,t = 0 .. T); |
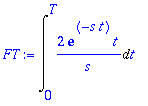
| > | u:=2/s*t; dv:=exp(-s*t): du:=diff(u,t): v:=int(dv,t); |
![]()
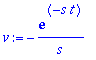
| > | FT:=subs(t=T,u*v)-subs(t=0,u*v)-Int(v*du,t=0..T); |
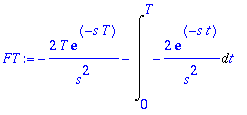
Jälleen eka termi menee 0:aan (kun s > 0), joten
| > | FT:=Int(2*exp(-s*t)/s^2,t = 0 .. T); |
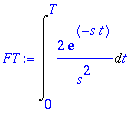
Tässä onkin pelkkä exp-funktion integraali. Annetaan nyt Maplen laskea se:
| > | value(FT); |
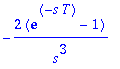
Siispä saadaan:
| > | F:=2/s^3; |
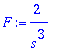
Tarkistus:
| > | int(f*exp(-s*t),t=0..infinity); |
Definite integration: Can't determine if the integral is convergent.
Need to know the sign of --> s
Will now try indefinite integration and then take limits.
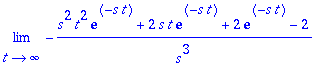
| > | assume(s > 0);int(f*exp(-s*t),t=0..infinity); |
![]()
| > | with(inttrans): |
| > | laplace(f,t,s); |
![]()
Onpa nyt ainakin varmennettu.
b)
| > | restart:with(inttrans):alias(L=laplace,IL=invlaplace): |
Warning, the name changecoords has been redefined
Malliratkaisuissa riittäköön a)-kohdan perusteellinen "vaiheistus". Antaa Maplen nyt integroida.
| > | f:=t*exp(-t); |
![]()
| > | intT:=int(f*exp(-s*t),t=0..T); |
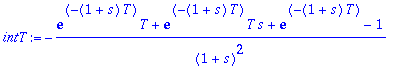
Kun s > -1 , saadaan raja-arvoksi:
| > | Limit('intT',T=infinity)=1/(1+s)^2; |
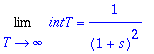
| > | L(f,t,s); # Tarkistus |
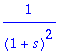
Lisätehtävä: Mieti, miten saat tämän s-siirtolauseen avulla!
c)
| > | f:=cos(a*t); |
![]()
| > | intT:=int(f*exp(-s*t),t=0..T); |
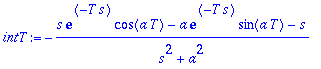
| > | Limit('intT',T=infinity)=s/(s^2+a^2); # kun s > 0 |
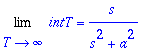
Katsotaan taulukosta, oikein on.
Kahdella peräkkäisellä osittaisintegroinnilla johdetaan yhtälö, josta integraali voidaan ratkaista.
d)
No tämä nyt on aivan samanlainen:
| > | f:=sin(a*t); |
![]()
| > | intT:=int(f*exp(-s*t),t=0..T); |
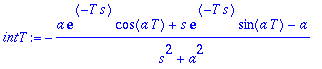
| > | Limit('intT',T=infinity)=a/(s^2+a^2); # kun s > 0 |
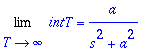
![[Maple Plot]](images/harj9lv30.gif)
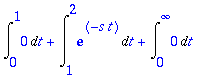
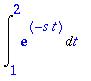
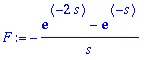
![[Maple Plot]](images/harj9lv34.gif)