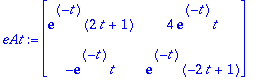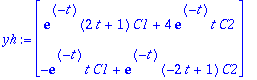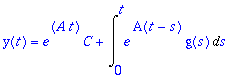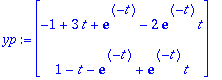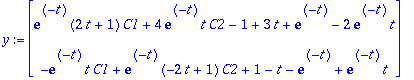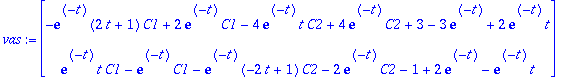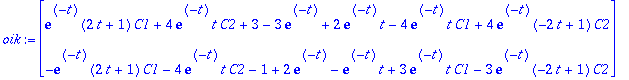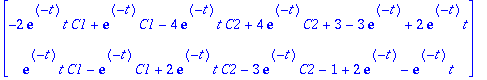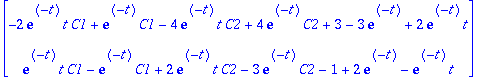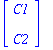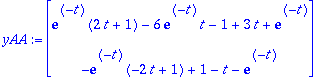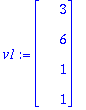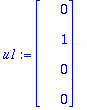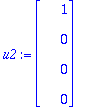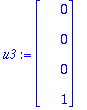Harj 8 LV
pe 8.11.02
Alustukset
| > |
restart:with(LinearAlgebra):with(linalg):
|
Warning, the name changecoords has been redefined
Warning, the previous binding of the name GramSchmidt has been removed and it now has an assigned value
Warning, the protected names norm and trace have been redefined and unprotected
| > |
alias(Id=IdentityMatrix):
|
| > |
alias(rref=ReducedRowEchelonForm): alias(Diag=DiagonalMatrix):alias(ref=GaussianElimination):
|
3.
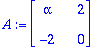
| > |
p:=det(A-lambda*Id(2));
|
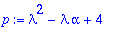
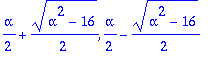
1)
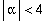 => kompleksijuuret, lähdefokus (epästabiili), jos
=> kompleksijuuret, lähdefokus (epästabiili), jos
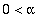 , nielufokus (stabiili), jos
, nielufokus (stabiili), jos
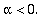 (Jos
(Jos
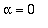 , saadaan keskus, joka on heikosti stabiili)
, saadaan keskus, joka on heikosti stabiili)
2)
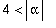
Molemmat ominaisarvot samanmerkkiset (tulo =4). Jos
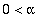 , niin positiiviset, jos
, niin positiiviset, jos
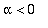 , negatiiviset.
, negatiiviset.
Siten alpha > 4 ==> lähde (epästabiili), alpha < 0 ==> nielu (stabiili).
Mielenkiintoisimmat ovat ehkä dgeneraatiotapaukset 4 ja -4.
Tällöin käytetään Cayley-Hamiltonia:
| > |
alpha:=4: lambda:=alpha/2;
|
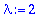
| > |
At:='lambda*t*Id(2)'+'t*(A-lambda*Id(2))';
|
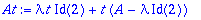
| > |
expAt:=exp(lambda*t)*(Id(2)+t*(A-lambda*Id(2)));
|
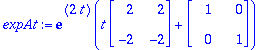
![matrix([[exp(2*t)*(2*t+1), 2*exp(2*t)*t], [-2*exp(2*t)*t, exp(2*t)*(-2*t+1)]])](images/harj8lv14.gif)
![matrix([[exp(2*t)+2*exp(2*t)*t, 2*exp(2*t)*t], [-2*exp(2*t)*t, exp(2*t)-2*exp(2*t)*t]])](images/harj8lv15.gif)
4.
a)
diag(d1,d2, .. dn)^k = diag(d1^k,d2^k,...,dn^k). (Diagonaalimatriisien kertolaskussa diagonaalialkiot kerrotaan keskenään.)
| > |
At:=<<t*d1,0>|<0,t*d2>>;
|
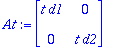
| > |
add((At^k)/k!,k=0..10);
|
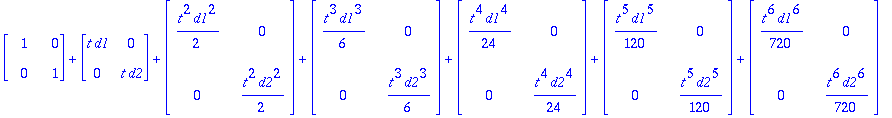
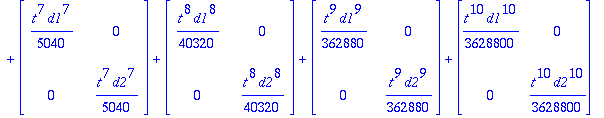
![matrix([[1+t*d1+1/2*t^2*d1^2+1/6*t^3*d1^3+1/24*t^4*d1^4+1/120*t^5*d1^5+1/720*t^6*d1^6+1/5040*t^7*d1^7+1/40320*t^8*d1^8+1/362880*t^9*d1^9+1/3628800*t^10*d1^10, 0], [0, 1+t*d2+1/2*t^2*d2^2+1/6*t^3*d2^3+1...](images/harj8lv19.gif)
Tässä näkyy selkeästi, miten matriisisarja muodostuu. Diagonaalialkiosarjat ovat
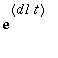 :n ja
:n ja
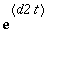 :n sarjoja. Eli:
:n sarjoja. Eli:
![matrix([[exp(t*d1), 0], [0, exp(t*d2)]])](images/harj8lv22.gif)
Tämä tietysti pätee yleisellä n:llä.
Tässä siis:
| > |
A:=<<1,0>|<0,2>>; exponential(A,t);
|
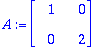
![matrix([[exp(t), 0], [0, exp(2*t)]])](images/harj8lv24.gif)
b.
| > |
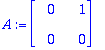
A:=<<0,0>|<1,0>>; At:=<<0,0>|<t*1,0>>; # LinearAlgebra on huono sieventelemään matriiislausekkeita. Siksi tämä At.
|
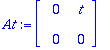
| > |
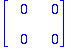
expAt:=Id(2)+At; # Tästä eteenpäin 0:aa
|
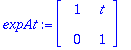
| > |
exponential(A,t); # Tarkistus
|
![matrix([[1, t], [0, 1]])](images/harj8lv29.gif)
c.)
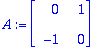
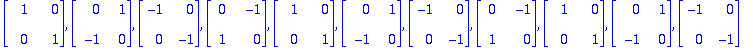
4:n pituinen jakso. Siitä nähdään kerroinjonot.
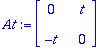
| > |
add((At^k)/k!,k=0..10);evalm(%);
|

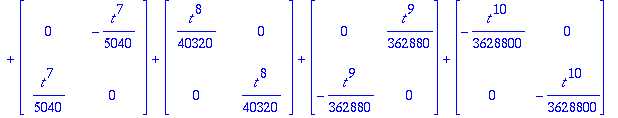
![matrix([[1-1/2*t^2+1/24*t^4-1/720*t^6+1/40320*t^8-1/3628800*t^10, t-1/6*t^3+1/120*t^5-1/5040*t^7+1/362880*t^9], [-t+1/6*t^3-1/120*t^5+1/5040*t^7-1/362880*t^9, 1-1/2*t^2+1/24*t^4-1/720*t^6+1/40320*t^8-1...](images/harj8lv35.gif)
Kun vielä kertomat otetaan mukaan, saadaan tällaisia osasummia alkiosarjoille, ts.
| > |
expAt:=<<cos(t),-sin(t)>|<sin(t),cos(t)>>;
|
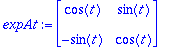
Toki voidaan myös diagonalisoida ja käyttää Eulerin kaavaa.
5.
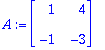
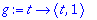
| > |
(lambda,ov):=Eigenvectors(A);
|
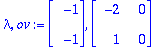
Lasketaan
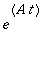 taiteen sääntöjen mukaan, vaikka tehtävässä ei vaadittu. (Olis kannattanut):
taiteen sääntöjen mukaan, vaikka tehtävässä ei vaadittu. (Olis kannattanut):
| > |
'A'*t=(-t)*'Id'+('A'+'Id')*t;
|
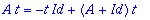
| > |
eAt:=exp(-t)*(Id(2)+(A+Id(2))*t);
|
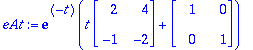
| > |
(A+Id(2))^2; # Toden totta, Cayley-Hamilton toimii!
|
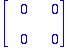
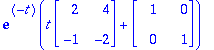
![eAt := matrix([[exp(-t)*(2*t+1), 4*exp(-t)*t], [-exp(-t)*t, exp(-t)*(-2*t+1)]])](images/harj8lv45.gif)
![matrix([[exp(-t)+2*exp(-t)*t, 4*exp(-t)*t], [-exp(-t)*t, exp(-t)-2*exp(-t)*t]])](images/harj8lv46.gif)
Saatiin sama!
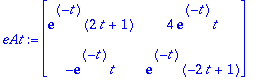
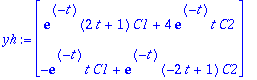
Sitten se kaunis EHY-kaava:
| > |
y(t)=e^('A'*t)*C+Int(e^'A(t-s)'*'g(s)',s=0..t); #tekstinkäsittelyä
|
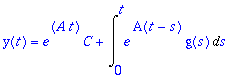
| > |
yp:=map(int,expA(t-s).g(s),s=0..t);
|
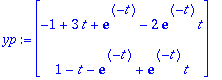
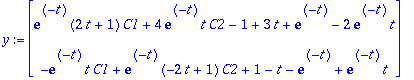
Tarkistetaan, että toteuttaa diffyhtälön:
| > |
vas:=map(diff,y,t); oik:=A.y+g(t);
|
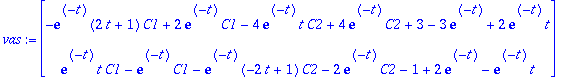
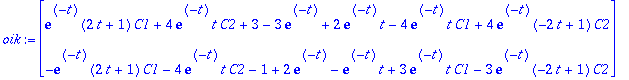
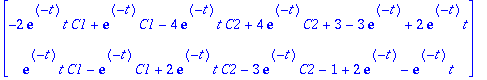
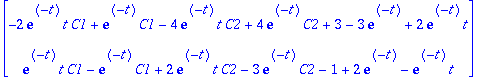
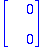
Hyvin kävi!
Sitten alkuehto:
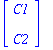
Voiko olla totta, no voi näinkin käydä. Siispä:
| > |
yAA:=subs(C1=1,C2=-1,y);
|
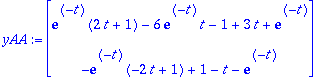
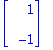
Niin se vaan on!
6.
| > |
A:=<<1,1,0,0>|<0,1,0,0>|<1,2,2,1>|<2,1,0,1>>;
|
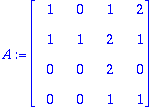
| > |
(lambda,ov):=Eigenvectors(A);
|
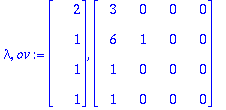
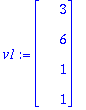
Etsitään ominaiarvoa 1 vastaavat yleistetyt ominaisvektorit:
| > |
u1:=ov[1..-1,2]; # Ensin se oikea ominaisvektori
|
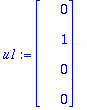
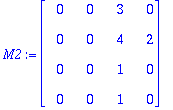
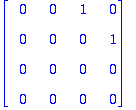
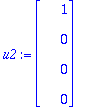
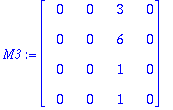
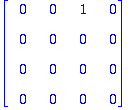
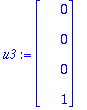
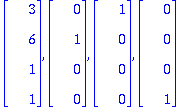
Tästä saadaan tulos, mutta nyt en enää ehdi kirjoitella.
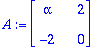
![]()
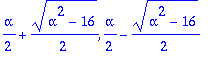
![]() => kompleksijuuret, lähdefokus (epästabiili), jos
=> kompleksijuuret, lähdefokus (epästabiili), jos
![]() , nielufokus (stabiili), jos
, nielufokus (stabiili), jos
![]() (Jos
(Jos
![]() , saadaan keskus, joka on heikosti stabiili)
, saadaan keskus, joka on heikosti stabiili)
![]()
![]() , niin positiiviset, jos
, niin positiiviset, jos
![]() , negatiiviset.
, negatiiviset.
![]()
![]()
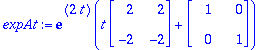
![matrix([[exp(2*t)*(2*t+1), 2*exp(2*t)*t], [-2*exp(2*t)*t, exp(2*t)*(-2*t+1)]])](images/harj8lv14.gif)
![matrix([[exp(2*t)+2*exp(2*t)*t, 2*exp(2*t)*t], [-2*exp(2*t)*t, exp(2*t)-2*exp(2*t)*t]])](images/harj8lv15.gif)
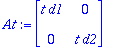
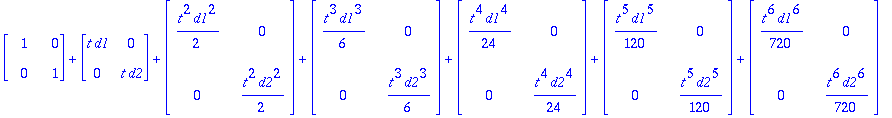
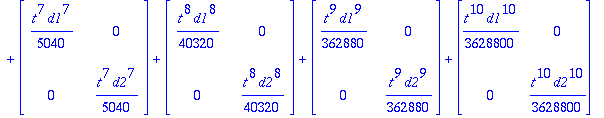
![matrix([[1+t*d1+1/2*t^2*d1^2+1/6*t^3*d1^3+1/24*t^4*d1^4+1/120*t^5*d1^5+1/720*t^6*d1^6+1/5040*t^7*d1^7+1/40320*t^8*d1^8+1/362880*t^9*d1^9+1/3628800*t^10*d1^10, 0], [0, 1+t*d2+1/2*t^2*d2^2+1/6*t^3*d2^3+1...](images/harj8lv19.gif)
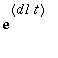 :n ja
:n ja
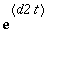 :n sarjoja. Eli:
:n sarjoja. Eli:
![matrix([[exp(t*d1), 0], [0, exp(t*d2)]])](images/harj8lv22.gif)
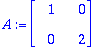
![matrix([[exp(t), 0], [0, exp(2*t)]])](images/harj8lv24.gif)

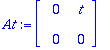

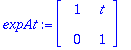
![matrix([[1, t], [0, 1]])](images/harj8lv29.gif)
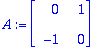
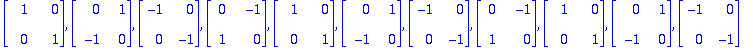
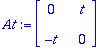

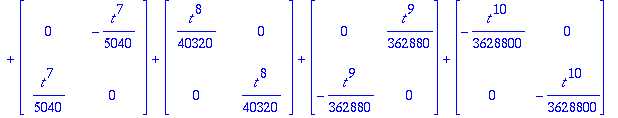
![matrix([[1-1/2*t^2+1/24*t^4-1/720*t^6+1/40320*t^8-1/3628800*t^10, t-1/6*t^3+1/120*t^5-1/5040*t^7+1/362880*t^9], [-t+1/6*t^3-1/120*t^5+1/5040*t^7-1/362880*t^9, 1-1/2*t^2+1/24*t^4-1/720*t^6+1/40320*t^8-1...](images/harj8lv35.gif)
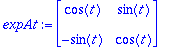
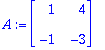
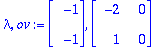
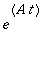 taiteen sääntöjen mukaan, vaikka tehtävässä ei vaadittu. (Olis kannattanut):
taiteen sääntöjen mukaan, vaikka tehtävässä ei vaadittu. (Olis kannattanut):
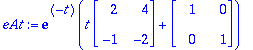

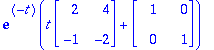
![eAt := matrix([[exp(-t)*(2*t+1), 4*exp(-t)*t], [-exp(-t)*t, exp(-t)*(-2*t+1)]])](images/harj8lv45.gif)
![matrix([[exp(-t)+2*exp(-t)*t, 4*exp(-t)*t], [-exp(-t)*t, exp(-t)-2*exp(-t)*t]])](images/harj8lv46.gif)