Harj. 8 AV
5.11.02, päivitetty 4.11.02
Lisänä käsinkirjoitettuja prujuja Astridin huoneen ovenpielessä.
Alustukset
1.
| > |
v1:=<-3,1>; v2:=<-1,1>;
|
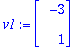
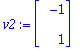
| > |
lambda[1]:=4: lambda[2]:=2;
|
![lambda[2] := 2](images/harj8av3.gif)
| > |
Y:=t->C1*exp(4*t)*v1+C2*exp(2*t)*v2;
|
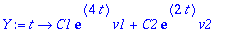
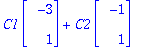
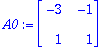
| > |
Ceet:=LinearSolve(A0,<-1,6>);
|
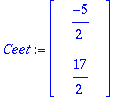
| > |
Yaa:=subs(C1=Ceet[1],C2=Ceet[2],Y(t));
|
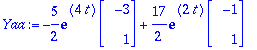
| > |
y1y2:=evalm(Yaa); # koordinaattimuodossa
|
![y1y2 := vector([15/2*exp(4*t)-17/2*exp(2*t), -5/2*exp(4*t)+17/2*exp(2*t)])](images/harj8av9.gif)
Kuvia ei vaadittu, mutta piirretän tässä. Huomaa parametripiirron syntaksi. (Kts. L12maple ja myös [HAM]-kirja)
| > |
plot([y1y2[1],y1y2[2],t=0..2]);
|
![[Maple Plot]](images/harj8av10.gif)
Tästä kuvasta ei paljon näy.
view
-optio on välttämätön:
| > |
plot([y1y2[1],y1y2[2],t=0..2],view=[-1..10,-10..10]);
|
![[Maple Plot]](images/harj8av11.gif)
| > |
plot([y1y2[1],y1y2[2],t=0..2],view=[10..200,-40..10]);
|
![[Maple Plot]](images/harj8av12.gif)
2.
| > |
restart: with(LinearAlgebra):
|
Warning, the name changecoords has been redefined
| > |
dyht:=diff(y(t),t,t)+0.125*diff(y(t),t)+y(t)=0;
|
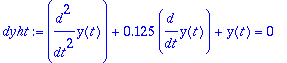
Merkitään
![y[1]](images/harj8av14.gif) = y,
= y,
![y[2]](images/harj8av15.gif) = y' , jolloin saadaan yhtälösysteemi:
= y' , jolloin saadaan yhtälösysteemi:
![y[1]](images/harj8av16.gif) ' =
' =
![y[2]](images/harj8av17.gif)
![y[2]](images/harj8av18.gif) ' =
' =
![-y[1]-.125*y[2]](images/harj8av19.gif)
| > |
A:=<<0,-1>|<1,-.125>>; A:=convert(A,rational);
|
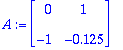
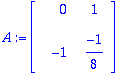
| > |
(Lambda,ov):=Eigenvectors(A);
|
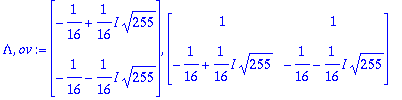
| > |
v1:=ov[1..-1,1]: v2:=ov[1..-1,2]:
|
| > |
y:=C1*exp(Lambda[1]*t)*v1+C2*exp(Lambda[2]*t)*v2;
|
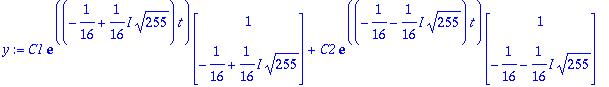
Tässä on kompleksimuoto. Reaaliseen kantaan pääsemiseksi voidaan tehdä vanhat temput:
| > |
lambda:=Lambda[1]; w:=ov[1..-1,1];
|
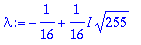
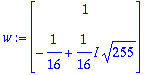
| > |
u:=map(Re,w); v:=map(Im,w);
|
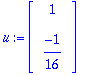
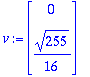
Kaavan johto lienee helpompi tehdä käsin kuin Maplella. Tässä on senverran hankalat lukuarvot, että on parempi johtaa yleisillä symboleilla:
| > |
alpha:='alpha': beta:='beta':
|
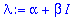
| > |
yr:=Re(exp(lambda*t)*(u+I*v)); yr:=evalc(%);
|
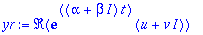
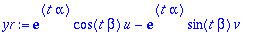
| > |
yi:=Im(exp(lambda*t)*(u+I*v)); yi:=evalc(%);
|
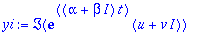
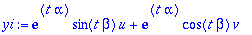
Perun heti puheeni. Kun sievennykset tehdään yleisillä symboleilla, menemättä vektorien komponentteihin, kaikki sujuu kuin rasvattu.
| > |
u:=map(Re,w); v:=map(Im,w);lambda:=Lambda[1]: alpha:=Re(lambda); beta:=Im(lambda);
|
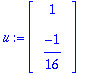
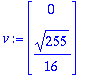
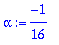
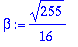
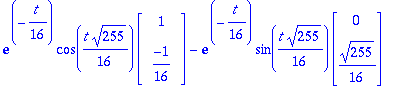
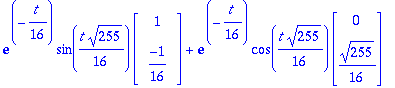
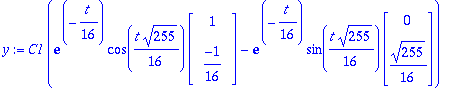
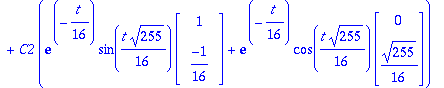
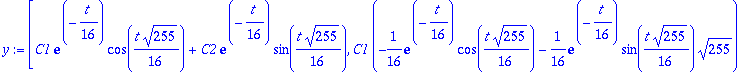
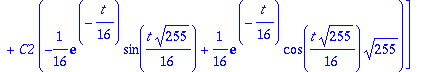
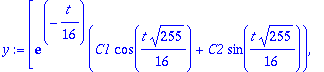
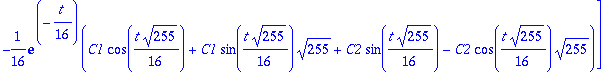
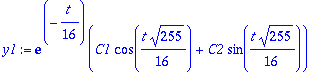
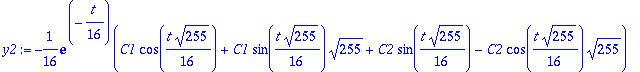
| > |
#dyht:=diff(y(t),t,t)+0.125*diff(y(t),t)+y(t)=0;
|
| > |
diff(y1,t,t)+0.125*diff(y1,t)+y1;
|
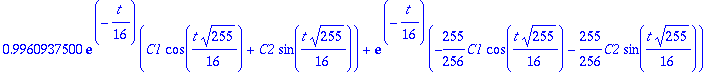

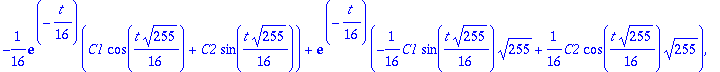
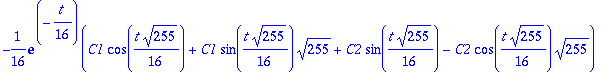
| > |
diff(y1,t)- y2: simplify(%);
|

Nuo kaksi nollaa kertovat kaiken. Systeemin ratkaisun 1. komponenttifunktio y1 toteuttaa dyht:n. Toinen komponentti on ensimmöisen derivaatta.
Ehkä hiukan huonosti harkittu käsinlaskuksi.
3.
| > |
A:=<<-2/25,2/25>|<1/50,-2/25>>;
|
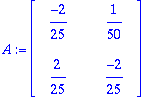
| > |
(lambda,V):=Eigenvectors(A);
|
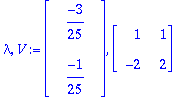
| > |
v1:=V[1..-1,1]: v2:=V[1..-1,2]:
|
| > |
y:=t->C1*exp(lambda[1]*t)*v1+C2*exp(lambda[2]*t)*v2;
|
![y := proc (t) options operator, arrow; C1*exp(lambda[1]*t)*v1+C2*exp(lambda[2]*t)*v2 end proc](images/harj8av54.gif)
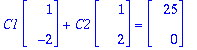
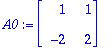
| > |
Ceet:=LinearSolve(A0,<2.5,0>);
|
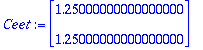
| > |
Y:=subs(C1=Ceet[1],C2=Ceet[2],y(t));
|
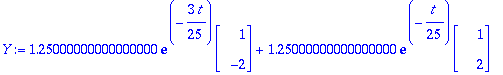
![ykoord := vector([1.25000000000000000*exp(-3/25*t)+1.25000000000000000*exp(-1/25*t), -2.500000000*exp(-3/25*t)+2.500000000*exp(-1/25*t)])](images/harj8av59.gif)
![ykoord := vector([1.25000000000000000*exp(-3/25*t)+1.25000000000000000*exp(-1/25*t), -2.500000000*exp(-3/25*t)+2.500000000*exp(-1/25*t)])](images/harj8av60.gif)
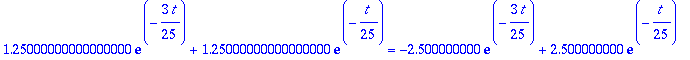
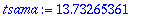
| > |
plot([ykoord[1],ykoord[2]],t=0..30);
|
![[Maple Plot]](images/harj8av63.gif)
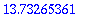
4.
Warning, the name changecoords has been redefined
| > |
with(plots): with(LinearAlgebra): with(linalg):
|
Warning, the previous binding of the name GramSchmidt has been removed and it now has an assigned value
Warning, the protected names norm and trace have been redefined and unprotected
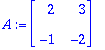
| > |
(lambda,V):=Eigenvectors(A);
|
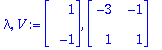
| > |
v1:=V[1..-1,1]; v2:=V[1..-1,2];
|
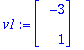
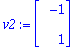
| > |
y:=t->C1*exp(lambda[1]*t)*v1+C2*exp(lambda[2]*t)*v2;
|
![y := proc (t) options operator, arrow; C1*exp(lambda[1]*t)*v1+C2*exp(lambda[2]*t)*v2 end proc](images/harj8av69.gif)
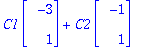
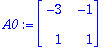
| > |
Ceet:=LinearSolve(A0,<3,2>);
|
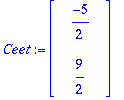
| > |
yAA:=subs(C1=Ceet[1],C2=Ceet[2],y(t));
|
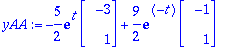
| > |
arrow([v1,v2],shape=arrow);
|
![[Maple Plot]](images/harj8av74.gif)
Ominaisvektorin v1 suunnalla trajektori kulkee poispäin O:sta, v2:n suunnalla O:oon päin.
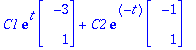
| > |
Ys:=map(eval,subs(t=log(s),y(t)));
|
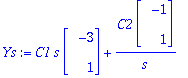
Selvästi hyperbelejä.
![YY := vector([-3*C1*s-C2/s, C1*s+C2/s])](images/harj8av77.gif)
| > |
parvi:=seq(seq([YY[1],YY[2],s=0..4],C2=-2..2),C1=-2..2):
|
![[Maple Plot]](images/harj8av78.gif)
| > |
display(%,arrow([v1,v2]),view=[-5..5,-5..5]);
|
![[Maple Plot]](images/harj8av79.gif)
Warning, the name adjoint has been redefined
| > |
display(kuva,DEplot([D(y1)(t)=2*y1(t)+3*y2(t),D(y2)(t)=-y1(t)-2*y2(t)],
[y1(t),y2(t)],t=-5..2,y1=-5..5,y2=-5..5,color=grey),title="Satula");
|
![[Maple Plot]](images/harj8av80.gif)
5.
Warning, the name changecoords has been redefined
| > |
with(plots): with(LinearAlgebra): with(linalg):
|
Warning, the previous binding of the name GramSchmidt has been removed and it now has an assigned value
Warning, the protected names norm and trace have been redefined and unprotected
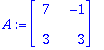
| > |
(lambda,V):=Eigenvectors(A);
|
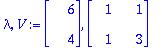
| > |
v1:=V[1..-1,1]; v2:=V[1..-1,2];
|
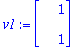
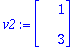
| > |
y:=t->C1*exp(lambda[1]*t)*v1+C2*exp(lambda[2]*t)*v2;
|
![y := proc (t) options operator, arrow; C1*exp(lambda[1]*t)*v1+C2*exp(lambda[2]*t)*v2 end proc](images/harj8av85.gif)
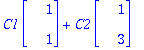
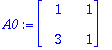
| > |
Ceet:=LinearSolve(A0,<3,2>);
|
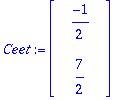
| > |
yAA:=subs(C1=Ceet[1],C2=Ceet[2],y(t));
|

| > |
arrow([v1,v2],shape=arrow);
|
![[Maple Plot]](images/harj8av90.gif)
Trajektorit kulkevat poispäin O:sta..
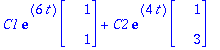
| > |
Ys:=map(eval,subs(t=log(s),y(t)));
|
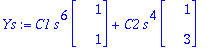
![YY := vector([C1*s^6+C2*s^4, C1*s^6+3*C2*s^4])](images/harj8av93.gif)
| > |
parvi:=seq(seq([YY[1],YY[2],s=0..4],C2=-2..2),C1=-2..2):
|
![[Maple Plot]](images/harj8av94.gif)
| > |
display(%,arrow([v1,v2]),view=[-5..5,-5..5]);
|
![[Maple Plot]](images/harj8av95.gif)
Warning, the name adjoint has been redefined
| > |
display(kuva,DEplot([D(y1)(t)=7*y1(t)-y2(t),D(y2)(t)=3*y1(t)+3*y2(t)],
[y1(t),y2(t)],t=-5..2,y1=-5..5,y2=-5..5,color=grey),title="Lähde");
|
![[Maple Plot]](images/harj8av96.gif)
![]()
![]()
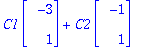
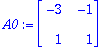
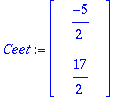
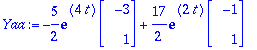
![]()
![[Maple Plot]](images/harj8av10.gif)
![[Maple Plot]](images/harj8av11.gif)
![[Maple Plot]](images/harj8av12.gif)
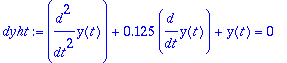
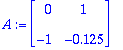
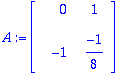
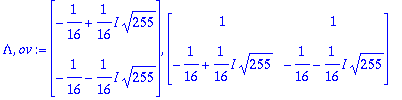
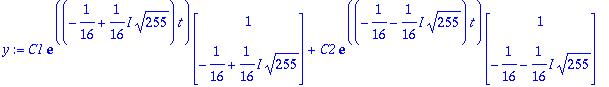
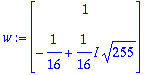
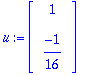
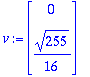
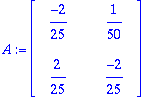

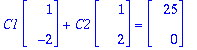
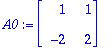
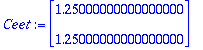
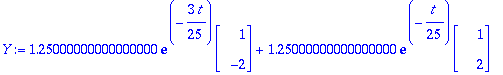
![ykoord := vector([1.25000000000000000*exp(-3/25*t)+1.25000000000000000*exp(-1/25*t), -2.500000000*exp(-3/25*t)+2.500000000*exp(-1/25*t)])](images/harj8av60.gif)
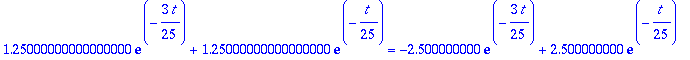
![[Maple Plot]](images/harj8av63.gif)
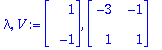
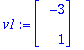
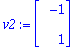
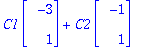
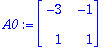
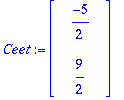
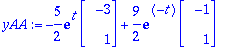
![[Maple Plot]](images/harj8av74.gif)
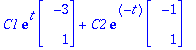
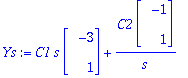
![[Maple Plot]](images/harj8av78.gif)
![[Maple Plot]](images/harj8av79.gif)
![[Maple Plot]](images/harj8av80.gif)
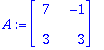
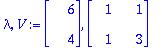
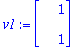
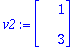
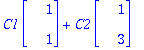
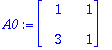
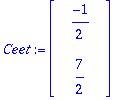

![[Maple Plot]](images/harj8av90.gif)
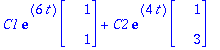
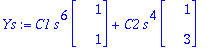
![[Maple Plot]](images/harj8av94.gif)
![[Maple Plot]](images/harj8av95.gif)
![[Maple Plot]](images/harj8av96.gif)