Harj 7 LV
V3, lokakuu 2002 HA
Alustukset
Tässäpä sattui hankala paikka.
Rita
oli miltei epätoivon partaalla, kun
GramSchmid
t ei toiminut, vaikka syöte
aivan varmasti oli oikea. Onnistuin nyt itsekin kaatumaan samaan seikkaan, vaikka aiemmin en ollut (ja ymmärsin omakohtaisesti
Ritan epätoivon).
Syy selvisi tarkkailemalla sinisiä latausvaroituksia;
"Warning, the previous binding of the name GramSchmidt has been removed and it now has an assigned value"
?GramSchmidt
paljastaa, että myös linalg:ssa on aivan samanniminen funktio. Nyt leikkisästi riippuu kirjastojen latausjärjesyksestä,
kumpi on voimassa.
Lupaan kirjoittaa tästä palautetta MUG-listalle ensi tilassa (Maple Users' Group).
Kohtuullisen robusti ratkaisu on alla oleva alias-määrittely, jossa viitataan koko nimeen kirjasto mukaanlukien.
Huomaa!
Aina voidaan käyttää pitkää nimeä, siis
LinearAlgebra[GramSchmidt],
jolloin kirjastoa ei edes tarvitse ladata. (Voidaan ajatella, että
LinearAlgebra
on ison perheen
sukunimi ja esim.
GramSchmid
t etunimi.)
| > |
alias(GS=LinearAlgebra[GramSchmidt]):
|
Warning, the protected names norm and trace have been redefined and unprotected
| > |
with(LinearAlgebra): with(linalg): with(plots):
|
Warning, the previous binding of the name GramSchmidt has been removed and it now has an assigned value
Warning, the protected names norm and trace have been redefined and unprotected
Warning, the name changecoords has been redefined
| > |
alias(ref=GaussianElimination):
|
| > |
sarakkeet:=A->[seq(A[1..-1,j],j=1..LinearAlgebra[Dimension](A)[2])]; # Tämä voi olla kätevä.
|
![sarakkeet := proc (A) options operator, arrow; [seq(A[1 .. -1,j],j = 1 .. LinearAlgebra[LinearAlgebra:-Dimension](A)[2])] end proc](images/harj7lv1.gif)
| > |
randV:=n->RandomVector(n,generator=rand(-1000..1000)/1000.);
|

| > |
randM:=(m,n)->RandomMatrix(m,n,generator=rand(-1000..1000)/1000.);
|
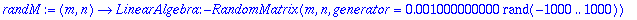
1.
| > |
A:=<<-6,-1,3,6,2,-3,-2,1>|<-3,2,6,-3,-1,6,-1,2>|<6,1,3,6,2,3,2,1>|<1,-6,-2,-1,3,2,-3,6>>;
|


Tämä on käyttäjän kannalta tehokkain tapa. Siinähän muodostetaan juuri kaikki sisätulot
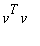 , missä
, missä
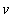 on
on
A:n sarakevektori.
Koska saatiin diagonaalimatriisi, on ortogonaalisuus osoitettu.
Nähdään myös, että jokaisen vektorin normi = 10, joten normaaraus saadaan yksinkertaisesti:

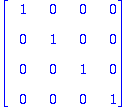
Tietenkään ortogonaalisen systeemin vektoreilla ei yleensä ole sama normi, joten normeeraus on tehtävä vektoreittain.
| > |
GS(sarakkeet(A)); # Käytetään nyt riemumielin GS:ää, vaikka ei tässä olekaan tarpeen.
|
![[Vector(%id = 134829864), Vector(%id = 134831912), Vector(%id = 134835288), Vector(%id = 134852640)]](images/harj7lv10.gif)
| > |
GS(sarakkeet(A),normalized);
|
![[Vector(%id = 134854400), Vector(%id = 134769684), Vector(%id = 134771892), Vector(%id = 134780308)]](images/harj7lv11.gif)
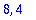
b)

Ainakin ne ovat eri kokoiset neliömatriisit. Kokeillaan nyt vielä tällaista:
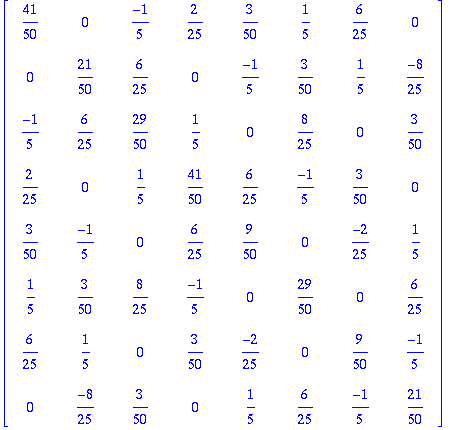
Ihmeellistä,
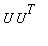 on sama kuin sen neliö. (Idempotentti.)
on sama kuin sen neliö. (Idempotentti.)
c)
Kun lasketaan
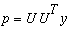 , niin vektorimuodossa kirjoitettuna saadaan :
, niin vektorimuodossa kirjoitettuna saadaan :
![eta[1]*u[1]](images/harj7lv17.gif) + ... +
+ ... +
![eta[m]*u[m]](images/harj7lv18.gif) ,
,
missä
![eta[k]](images/harj7lv19.gif) =<
=<
![u[k]](images/harj7lv20.gif) ,y>, ja
,y>, ja
![u[k]](images/harj7lv21.gif) on U:n k:s sarakevektori,
on U:n k:s sarakevektori,
Mieti tämä läpi kynän ja paperin kanssa.
U:n sarakkeet ovat A:n sarakkeet ortonormeerattuina, joten ne virittävät saman aliavaruuden, joka on (määritelmän mukaan)
A:n sarakeavaruus.
Toinen tapa olisi käyttää ref:iä:

Luokkaa 10^-16 oleva luku on ilman muuta nolla. Liitännäismatriisin rangi pysyy samana kuin A:n, joten
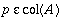 :
:
Tässä siis ref ei ollut tarpeen, koska ortogonaalisuus antoi tiedon suoraan.
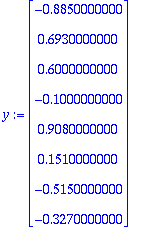
p on y:n ortog. projektio aliavaruudella col(A), joten se on yleisen projektiolauseen mukaan sellainen, että
(y - p) _|_ col(A)
Lasketaan nyt tässä tapauksessa vielä:

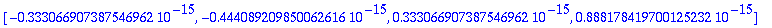
Vektorin z sisätulo jokaisen sarakkeen kanssa = 0, joten z on todellakin kohtisuorassa koko aliavaruutta col(A) vastaan
(vrt. teht. 1 AV, "lapsellinen lause").
d) Tämä esitys on avainasemassa moneen asiaan. Me osaamme ainakin�nähdä p:n PNS-approksimaationa y:lle.
2.
| > |
data:=[[4,1.58],[6,2.08],[8,2.5],[10,2.8],[12,3.1],[14,3.4],[16,3.8],[18,4.32]];
|
![data := [[4, 1.58], [6, 2.08], [8, 2.5], [10, 2.8], [12, 3.1], [14, 3.4], [16, 3.8], [18, 4.32]]](images/harj7lv27.gif)
| > |
xd:=map(p->p[1],data);yd:=map(p->p[2],data);
|
![xd := [4, 6, 8, 10, 12, 14, 16, 18]](images/harj7lv28.gif)
![yd := [1.58, 2.08, 2.5, 2.8, 3.1, 3.4, 3.8, 4.32]](images/harj7lv29.gif)
| > |
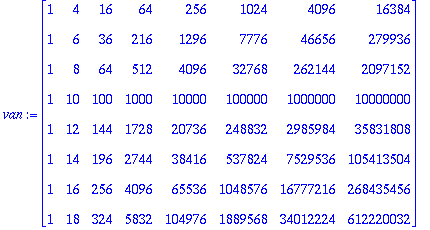
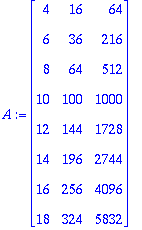
van:=VandermondeMatrix(xd);
|

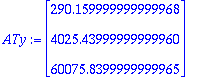
| > |
c:=LinearSolve(ATA,ATy); # Normaaliyhtälöt
|
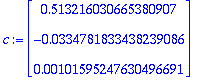
| > |
p:=c[1]*x+c[2]*x^2 + c[3]*x^3;
|
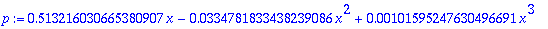
| > |
display(plot(data,style=point,symbol=cross,symbolsize=15),plot(p,x=4..18,color=grey));
|
![[Maple Plot]](images/harj7lv36.gif)
Tehdään vielä QR-hajotelmalla:
| > |
vvv:=seq(A[1..-1,j],j=1..3);
|
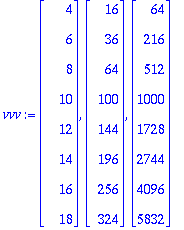
| > |
Q:=Matrix(GS([vvv],normalized));
|


| > |
cqr:=LinearSolve(R,TR(Q).<yd>);
|

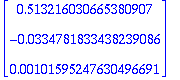
Varsin hyvällä tarkkuudella samat.
3. Pariisin lämpötilat
Ylimmät
Kirjoitetaan matriisi 2-sarakkeiseksi, tehtäväpaperissa on transponoitu näyttösyistä
| > |
Pariisi:=<<55,55,59,64,68,75,81,81,77,70,63,55>|<39,41,45,46,55,61,64,64,61,54,46,41>>;
|

| > |
Pariisi:=map(evalf@convert,Pariisi,temperature,degF,degC):
|
| > |
Paryla:=Pariisi[1..-1,1]; Parala:=Pariisi[1..-1,2];
|


| > |
TR(Paryla[1..10]); # Tässä on näköjään näytön raja.
|

Sovitetaan aineistoon malli, joka on jaksollinen, jaksona 12.
| > |
f:=(c,T)->c[1]+c[2]*cos(2*Pi*T/12)+c[3]*sin(2*Pi*T/12);
|
![f := proc (c, T) options operator, arrow; c[1]+c[2]*cos(1/6*Pi*T)+c[3]*sin(1/6*Pi*T) end proc](images/harj7lv46.gif)
| > |
Taulukko:=<<seq(i,i=1..12)>|Paryla>;
|



| > |
v1:=<seq(1,i=1..12)>;v2:=map(T->cos(2*Pi*T/12),T1);v3:=map(T->sin(2*Pi*T/12),T1);
|




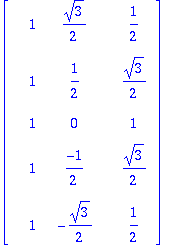
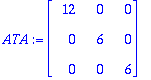
| > |
ATA.c=TR(A).Paryla: # Normaaliyhtälöt
|
| > |
c:=LinearSolve(ATA,TR(A).Paryla);
|
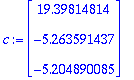

| > |
<<seq(i,i=1..12)>|Paryla>: yladata:=convert(%,listlist);
|
![yladata := [[1, 12.77777778], [2, 12.77777778], [3, 15.], [4, 17.77777778], [5, 20.], [6, 23.88888889], [7, 27.22222222], [8, 27.22222222], [9, 25.], [10, 21.11111111], [11, 17.22222222], [12, 12.77777...](images/harj7lv58.gif)
![yladata := [[1, 12.77777778], [2, 12.77777778], [3, 15.], [4, 17.77777778], [5, 20.], [6, 23.88888889], [7, 27.22222222], [8, 27.22222222], [9, 25.], [10, 21.11111111], [11, 17.22222222], [12, 12.77777...](images/harj7lv59.gif)
Tässä oli näppärä temppu, jolla matriisi saadaan vaakarivien (listojen) listaksi. (Matriisin luonteva tietorakenne
"listakielessä" olisi listojen lista.)
| > |
display(plot(yladata,style=point),plot(f(c,t),t=1..12,color=grey),title="Pariisin ylimpiin lämpötiloihin sovitettu trig. polynomi");
|
![[Maple Plot]](images/harj7lv60.gif)
Alimmat
| > |
Pariisi:=<<55,55,59,64,68,75,81,81,77,70,63,55>|<39,41,45,46,55,61,64,64,61,54,46,41>>;
|

| > |
Pariisi:=map(evalf@convert,Pariisi,temperature,degF,degC):
|
| > |
Parala:=Pariisi[1..-1,2];
|

Sovitetaan aineistoon malli, joka on jaksollinen, jaksona 12.
| > |
f:=(c,T)->c[1]+c[2]*cos(2*Pi*T/12)+c[3]*sin(2*Pi*T/12);
|
![f := proc (c, T) options operator, arrow; c[1]+c[2]*cos(1/6*Pi*T)+c[3]*sin(1/6*Pi*T) end proc](images/harj7lv63.gif)
| > |
Taulukko:=<<seq(i,i=1..12)>|Parala>:
|
| > |
#Taulukko[1..10,1..-1];
|
| > |
v1:=<seq(1,i=1..12)>:v2:=map(T->cos(2*Pi*T/12),T1):v3:=map(T->sin(2*Pi*T/12),T1):
|
| > |
#ATA.c=TR(A).Paryla: # Normaaliyhtälöt
|
| > |
c:=LinearSolve(ATA,TR(A).Parala);
|
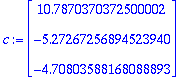

| > |
<<seq(i,i=1..12)>|Parala>: aladata:=convert(%,listlist);
|
![aladata := [[1, 3.888888889], [2, 5.], [3, 7.222222222], [4, 7.777777778], [5, 12.77777778], [6, 16.11111111], [7, 17.77777778], [8, 17.77777778], [9, 16.11111111], [10, 12.22222222], [11, 7.777777778]...](images/harj7lv66.gif)
![aladata := [[1, 3.888888889], [2, 5.], [3, 7.222222222], [4, 7.777777778], [5, 12.77777778], [6, 16.11111111], [7, 17.77777778], [8, 17.77777778], [9, 16.11111111], [10, 12.22222222], [11, 7.777777778]...](images/harj7lv67.gif)
| > |
display(plot(aladata,style=point),plot(f(c,t),t=1..12,color=grey),title="Pariisin alimpiin lämpötiloihin sovitettu trig. polynomi");
|
![[Maple Plot]](images/harj7lv68.gif)
Pahoittelut:
Harjoituksissa (to) esitin matriisin rakentamisen taululla ihan asiallisesti, mutta sen rakentaminen Maplella
meni vikaan, koska ykkössarakkeen sijaan otin epähuomiossa kuukausisarakkeen (1..12). (Näppäimistön äärellä
pääsi unohtumaan se, mitä pitikään rakentaa.)
Kuvat eivät sitten onnistuneet. Valitan joidenkin kohdalla hukkaan mennyttä aikaa.
6.
Warning, the name changecoords has been redefined
| > |
vasen:=m*diff(y(t),t,t)+c*diff(y(t),t)+k*y(t);
|
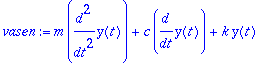
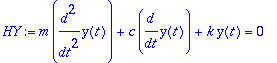
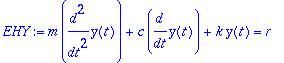
Lasketaan muutakin kuin "steady state". Olkoon tämä teoriaa kertaava ja täydentävä esimerkkiratkaisu.
1) HY:n yleinen ratkaisu:
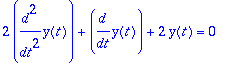
| > |
karyht:=2*lambda^2+lambda+2=0;
|
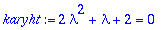
| > |
lam:=solve(karyht,lambda);
|
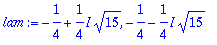
| > |
alpha:=Re(lam[1]); beta:=abs(Im(lam[1])); # abs vain siksi, että Maple voi saada päähänsä vaihtaa lam-jonon alkioiden järjestystä eri ajokerroilla.
|
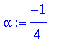
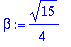
HY:n yleinen on siis:
| > |
yh:=exp(alpha*t)*(A*cos(beta*t)+B*sin(beta*t));
|
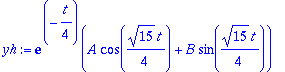
Siinä se komeilee! Vakiot A ja B määräytyvät alkuehdoista.
Mutta, alkuehtoja ei sovelleta HY:öön,
kun
yhtälömme
on EHY
. (Jos kyse olisi vapaasta, siis ilman ulkoista voimaa olevasta värähtelystä, niin silloin (ja vain silloin)...)
Joka tapauksessa, olivatpa alkuehdoista saatavat vakiot A ja B mitä tahansa, niin
](images/harj7lv78.gif) --> 0, kun t -->
--> 0, kun t -->
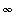 .
.
Siksi yh:ta sanotaan transientiksi, se edustaa nopeasti nitisyvää alkuvaihetta, joka siis negatiiviseksponenttisen exp-
funktion ansiosta pian kuolee pois.
Katsotaan, miten Maplen dsolve - komentoa käytettäisiin:
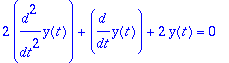
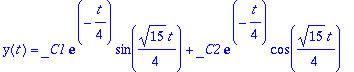
2. EHY:n erikoinen:
| > |
r:=3*cos(3*t)-2*sin(3*t):
|
Koska ulkoisen voiman (herätteen) taajuus ei yhdy HY:n ratkaisun taajuuteen, niin "teoriasta" tiedämme jo etukäteen,
että samantaajuinen sin/cos-värähtely johtaa tulokseen. Ts. alla oleva yrite toimii.
| > |
yp:=a*cos(3*t)+b*sin(3*t);
|
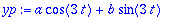
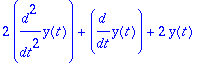
| > |
yriteyhtalo:=eval(subs(y(t)=yp,vasen))=r;
|
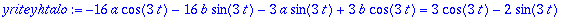
| > |
vas:=lhs(yriteyhtalo): oik:=rhs(yriteyhtalo):
|
cos-termien kertoimet samat, sin-termien kertoimet samat:
| > |
kerroinyhtalot:=coeff(vas,cos(3*t))=coeff(oik,cos(3*t)),coeff(vas,sin(3*t))=coeff(oik,sin(3*t));
|
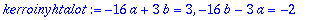
| > |
ab:=solve({kerroinyhtalot},{a,b});
|
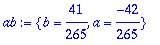
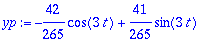
Tätä kutsutaan
tasapainotilaratkaisuksi ("steady state")
, pitkällä aikavälillä yhtälön ratkaisu on hyvin tarkkaan tämä
(mitä suurempi t, sen tarkempi), alkuarvoista riippumatta.
Kirjoitetaan muotoon: Vaihekulma ja amplitudi.
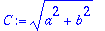
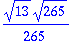

| > |
C:=evalf(C); delta:=evalf(delta);
|
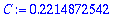

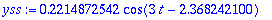
Alkuehdot:
Muutetaan ratkaisulauseke funktioiksi, jotta alkuehdot olisi kätevä muodostaa.
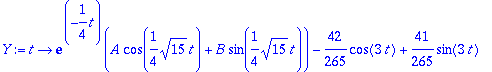
| > |
solve({Y(0)=1,D(Y)(0)=0},{A,B});
|
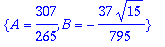
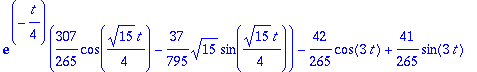
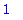

| > |
plot([r,Y(t),yp],t=0..15,color=[red,green,blue],title="Vaimennettu pakkovärähtely",legend=["Heräte (r(t))","Vaste (Y=yh+yp)","Tasapainotila (yp)"]);
|
![[Maple Plot]](images/harj7lv99.gif)
| > |
plot([r,Y(t),yp],t=0..15,color=[red,green,blue],legend=[p,g,oo]);
|
![[Maple Plot]](images/harj7lv100.gif)
![]()
![]()
![]()




![[Vector(%id = 134829864), Vector(%id = 134831912), Vector(%id = 134835288), Vector(%id = 134852640)]](images/harj7lv10.gif)
![[Vector(%id = 134854400), Vector(%id = 134769684), Vector(%id = 134771892), Vector(%id = 134780308)]](images/harj7lv11.gif)








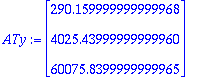
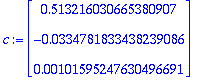
![[Maple Plot]](images/harj7lv36.gif)




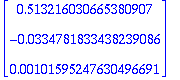











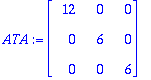
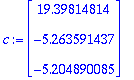
![[Maple Plot]](images/harj7lv60.gif)


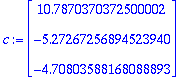
![[Maple Plot]](images/harj7lv68.gif)
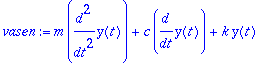
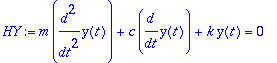
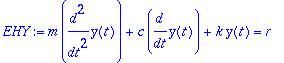
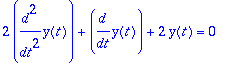
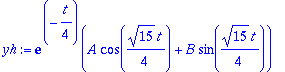
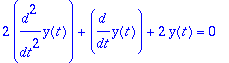
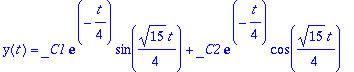
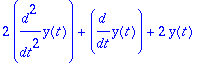
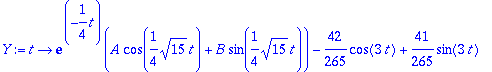
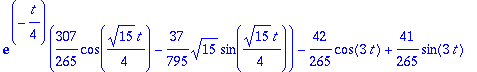
![[Maple Plot]](images/harj7lv99.gif)
![[Maple Plot]](images/harj7lv100.gif)