Harj 7 AV
ti 29.10.02
Ratkaisuihin liittyy käsinkirjoitettu pruju, joka on jaossa luennoilla ja saatavissa myös Astridin huoneen ovenpielestä.
Alustukset
| > |
with(linalg):
with(LinearAlgebra):
|
Warning, the protected names norm and trace have been redefined and unprotected
Warning, the assigned name GramSchmidt now has a global binding
| > |
alias(GS=LinearAlgebra[GramSchmidt]): # Huomaa tämä!
|
| > |
alias(TR=LinearAlgebra[Transpose]):
|
| > |
alias(rref=ReducedRowEchelonForm): alias(ref=GaussianElimination): alias(Diag=DiagonalMatrix,Id=IdentityMatrix):
with(plots):
|
| > |
alias(Dot=DotProduct,Id=IdentityMatrix,TR=Transpose):
|
| > |
Sis:=(u,v)->add(u[i_]*conjugate(v[i_]),i_=1..LinearAlgebra[Dimension](u)):
|
1.
Käsin kirjoitettu pruju.
2.
Kts. myös pruju.
| > |
A:=<<1,1,1,1>|<-1,4,-1,4>>;
|
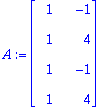
| > |
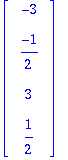
Q:=GramSchmidt([A[1..-1,1],A[1..-1,2]],normalized);
|
![Q := [Vector(%id = 135861452), Vector(%id = 138847196)]](images/harj7av2.gif)
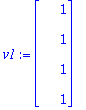
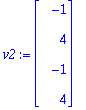
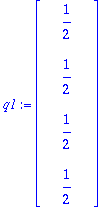
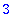
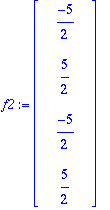
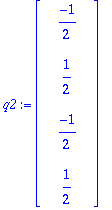
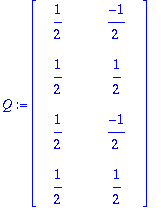
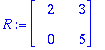
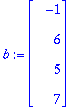
Prujussa on esitetty, miten R-matriisi saadaan suoraan GS-prosessin tuottamista kertoimista.
Tässä on tehty "halpahintaiseen" tyyliin.
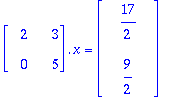
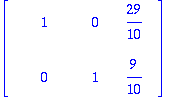
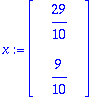
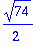
3.
Pruju.
4.
| > |
karpoly:=8*lambda^2-2*lambda-1;
|
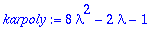
| > |
Lambda:=solve(karpoly=0,lambda);
|
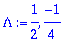
| > |
y:=C1*exp(Lambda[1]*t)+C2*exp(Lambda[2]*t);
|
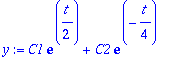
Tässä on yhtälön (HY) yleinen ratkaisu.
Alkuehdot saadaan sijoittamalla t:lle arvo 0 y:n ja diff(y,t):n lausekkeissa.
(Maple-huom: Emme voi kirjoittaa y(0), koska y on vain t:n lauseke eikä Maple-funktio.)
| > |
AE:={subs(t=0,y)=-0.2,subs(t=0,diff(y,t))=-0.325};
|
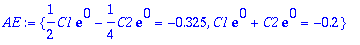
| > |
Ceet:=solve(AE,{C1,C2});
|

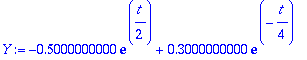
Tässä on AA-tehtävämme ratkaisu.
Tarkistus:
| > |
subs(t=0,Y), subs(t=0,diff(Y,t));
|
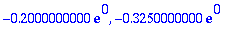
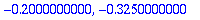
Alkuehdot toteutuvat.
Sitten diffyhtälö:
| > |
8*diff(Y,t,t)-2*diff(Y,t)-Y;
|

Sekin toteutuu, joten kaikki on kunnossa.
5.
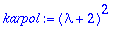
Tarkistetaan:
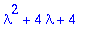
Koska
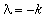 on kaksinkertainen juuri, saadaan toinen LRT ratkaisu kertomalla t:llä. ("perimätieto").
on kaksinkertainen juuri, saadaan toinen LRT ratkaisu kertomalla t:llä. ("perimätieto").
Yleinen ratkaisu on siten:
| > |
y:=(C1+t*C2)*exp(-k*t);
|
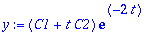
6.
Warning, the name changecoords has been redefined
| > |
karpol:=lambda^2+4*lambda+13;
|
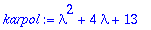
| > |
Lambda:=solve(karpol=0,lambda);
|
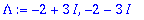
| > |
alpha:=Re(Lambda[1]); beta:=abs(Im(Lambda[1]));
|
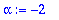
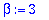
Suosimme positiivista beta:aa. Koska Maple saattaa muutella järjestystä, otimme abs:n mukaan peliin. Sinänsä
yleinen ratkaisu ei muutu, otettiinpa kumpi tahansa.
| > |
yh:=exp(alpha*t)*(A*cos(beta*t)+B*sin(beta*t));
|
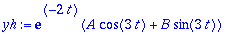
EHY:n erikoista kannattaa etsiä "herätteen" taajuuksisen trig. polynomin muodossa (koska tällainen ei toteuta HY:öä).
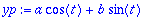
| > |
dyht:=diff(yp,t,t)+4*diff(yp,t)+13*yp=cos(t);
|
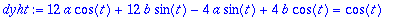
Yhtälön vasen puoli:
lhs, "left hand side"
, vastaavasti
oikea puoli: rhs
.
cos- ja sin-termien kertoimien oltava samat:
| > |
abyht:=coeff(lhs(dyht),cos(t))=1,coeff(lhs(dyht),sin(t))=0;
|
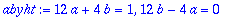
| > |
ab:=solve({abyht},{a,b});
|
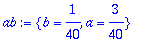
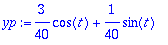
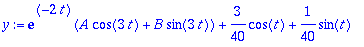
Alkuehdot voitaisiin käsitellä subs-tyylillä, kuten edellä. Vielä kätevämpää on muuttaa lauseke funktioksi
unapply
:lla:
Warning, premature end of input
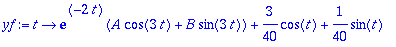
| > |
AB:=solve({yf(0)=0,D(yf)(0)=1},{A,B});
|
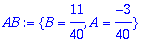
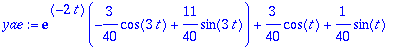
![[Maple Plot]](images/harj7av44.gif)
| > |
plot([yae,yp],t=0..20);
|
![[Maple Plot]](images/harj7av45.gif)
Ajanhetkestä t=2 lähtien yaa ja yp eivät kuvan tarkkuudella erotu toisistaan.

![Q := [Vector(%id = 135861452), Vector(%id = 138847196)]](images/harj7av2.gif)
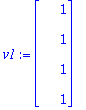
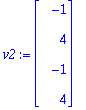
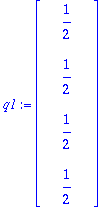
![]()
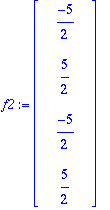
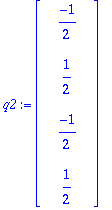
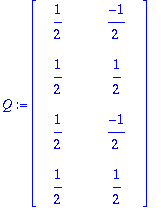

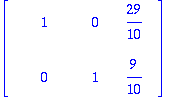
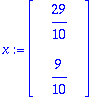

![]()
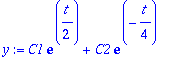
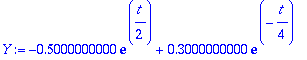
![[Maple Plot]](images/harj7av44.gif)
![[Maple Plot]](images/harj7av45.gif)