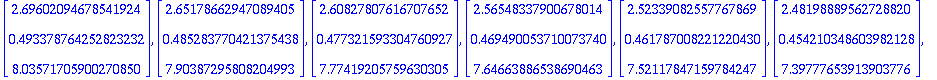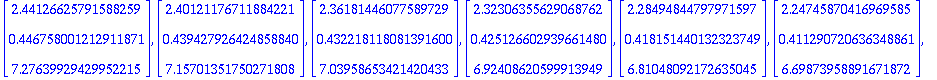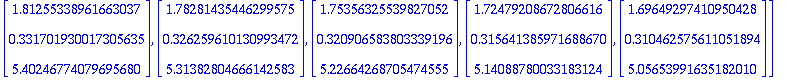Alustukset, ohjelmat
| > | read("/home/apiola/opetus/peruskurssi/v2-3/302/L/v302.mpl"); |
![]()
![]()
![]()
| > | # read("/p/edu/mat-1.414/maple/v302.mpl"); # Poista kommentti tästä ja lisää edelle! |
| > | #read("c:\\usr\\heikki\\s02\\v302.mpl"); |
| > | with(LinearAlgebra): with(plots): |
| > | op(trajenuoli); |
![]()
![]()
![]()
![]()
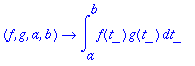
![[Maple Plot]](images/harj6lv15.gif)
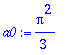
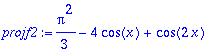
![[Maple Plot]](images/harj6lv22.gif)
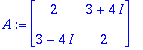
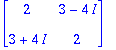
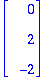
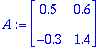
![[Maple Plot]](images/harj6lv35.gif)
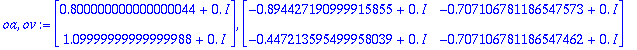
![[Maple Plot]](images/harj6lv38.gif)
![[Vector(%id = 134770068), Matrix(%id = 134874496)]](images/harj6lv39.gif)
![[Maple Plot]](images/harj6lv40.gif)
![[Maple Plot]](images/harj6lv41.gif)
![[Maple Plot]](images/harj6lv42.gif)
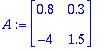
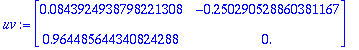
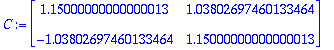

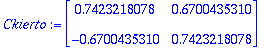
![[Maple Plot]](images/harj6lv57.gif)
![[Maple Plot]](images/harj6lv58.gif)
![[Maple Plot]](images/harj6lv59.gif)
![[Maple Plot]](images/harj6lv60.gif)


![x[k] = Vector(%id = 135093208)](images/harj6lv63.gif)
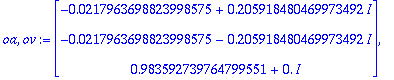

![[Maple Plot]](images/harj6lv76.gif)


![[Maple Plot]](images/harj6lv82.gif)