Harj. 6 AV
22.10.02
Alustukset
Warning, the name changecoords has been redefined
| > |
alias(ref=GaussianElimination):
|
| > |
alias(Dot=DotProduct,Id=IdentityMatrix):
|
Konjugointisäännöt DotProduct:ssa ova niin mutkikkaat ja monitahoiset, että on verrattomasti helpompaa määritellä
suosiolla oma Sis-funktio sisätuloksi. (Lokalisointipuutteen takia käytetään "outoja" nimiä, kuten i_ )
| > |
Sis:=(u,v)->add(u[i_]*conjugate(v[i_]),i_=1..LinearAlgebra[Dimension](u));
|
![Sis := proc (u, v) options operator, arrow; add(u[i_]*conjugate(v[i_]),i_ = 1 .. LinearAlgebra[LinearAlgebra:-Dimension](u)) end proc](images/harj6av1.gif)
1.
| > |
with(LinearAlgebra):alias(Id=IdentityMatrix):
|
| > |
Sis:=(u,v)->add(u[i_]*conjugate(v[i_]),i_=1..LinearAlgebra[Dimension](u));
|
![Sis := proc (u, v) options operator, arrow; add(u[i_]*conjugate(v[i_]),i_ = 1 .. LinearAlgebra[LinearAlgebra:-Dimension](u)) end proc](images/harj6av2.gif)
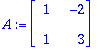
| > |
p:=Determinant(A-lambda*Id(2));
|
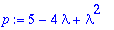
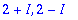
Käsinlasku:
| > |
lambda:=2+I: w:=<-2,1+I>;
|
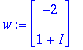
| > |
u:=map(Re,w); v:=map(Im,w);
|
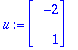
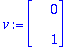
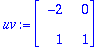
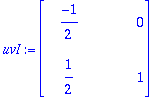
| > |
alpha:=Re(lambda): beta:=Im(lambda):
|
| > |
C:=<<alpha,-beta>|<beta,alpha>>;
|
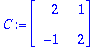
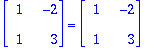
Siinäpä se taas kerran!
Annetaan mennä vielä Maplella kokonaan:
| > |
(oa,ov):=Eigenvectors(A);
|
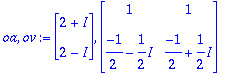
| > |
lambda:=oa[1]: w:=ov[1..-1,1];
|
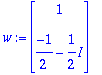
| > |
u:=map(Re,w): v:=map(Im,w);
|
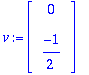
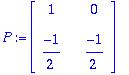
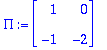
Jos ollaan laiskoja, niin C voidaan ratkaista näin halpahintaisesti:
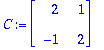
Huom 1:
C-matriisi on yksikäsitteinen (järjestystä vaille). P:n sarakkeet ovat ominaisvektoreita. Ne voidaan normeerata miten hyvänsä.
Normeeraus vaikuttaa kääneismatriisiin ("kompenspoivalla normaarauksella").
Huom 2
: Jos P:n sarakkeet otetaan järjestyksessä
<v | u >
, niin C:n sivulävistäjän merkit vaihtavat paikkaa. Tämä on se toinen muoto, joka edllisessä harjoituksessa
aiheutti kiusaa. Kokeile harjoituksen vuoksi johtaa kaavaa niinpän, niin näet.
Warning, premature end of input
2.
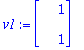
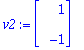
| > |
lambda[1]:=3: lambda[2]:=1/3:
|
| > |
x[k]=c[1]*3^k*v1+c[2]*(1/3)^k*v2;
|
![x[k] = c[1]*3^k*Vector(%id = 140812236)+c[2]*(1/3)^k*Vector(%id = 138553320)](images/harj6av21.gif)
Trajektorit {v1,v2}-koordinaatistossa toteuttavat siten ehdon
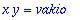
Jos siis merkitään koordinaatteja tättä ov-koordinaatistossa (x,y). Saadaan siis ihan tavallinen hyperbeliparvi.
Esitetään ominaisvektorikoordinaatistossa, joka kierretään oikeaan asentoon käyttämällä 3d-piirtoa. (2d-plotilla ei onnistu näin, silloin pitäisi kierto kohdistaa dataan,
mikä on hiukan vaivalloisempaa). Kannattaa toki huomata, että tämä mentelmä soveltuu vain silloin, kun kysessä on koordinaatiston kierto. Jos akselien kulma ja/tai skaalat muuttuvat,
on ominaisvektorimatriisin antamaa kannanvaihtomuunnosta sovellettava dataan.
| > |
display(spacecurve([x,1/x,0,x=.1..10]),spacecurve([x,-1/x,0,x=.1..10]),spacecurve([-x,1/x,0,x=.1..10]),spacecurve([-x,-1/x,0,x=.1..10]),axes=boxed,orientation=[-135,1]);
|
![[Maple Plot]](images/harj6av23.gif)
Kannattaa täydentää käsin. Alkupisteet kannattaa valita ensin ominaisvektoreilta ja piirtää suuntanuolet.
Sitten esim. pisteet (1,1), (-1,1) , (1,-1), (-1,-1). Tässä tapauksessa saadaan suoraan muotoa y=C/x oleva käyräparvi ominaisvektorikoordinaatistossa.
Sitä yllä olevassa piirroksessa on käytetty.
3.
A:n diagonalisointi on annettu, siitä saadaan itse A vain kertolaskulla (ja käänteismatriisin muodostuksella).
Warning, the name changecoords has been redefined
| > |
with(LinearAlgebra): Sis:=(u,v)->add(u[i_]*conjugate(v[i_]),i_=1..Dimension(u));
|
![Sis := proc (u, v) options operator, arrow; add(u[i_]*conjugate(v[i_]),i_ = 1 .. LinearAlgebra:-Dimension(u)) end proc](images/harj6av24.gif)
| > |
A.v[1]=lambda[1]*v[1]; A.v[2]=lambda[2]*v[2];
|
![A.v[1] = lambda[1]*v[1]](images/harj6av25.gif)
![A.v[2] = lambda[2]*v[2]](images/harj6av26.gif)
| > |
![A.`<|>`(v[1],v[2]) = `<|>`(lambda[1]*v[1],lambda[2]*v[2])](images/harj6av27.gif)
|
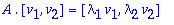
Tästä saadaan A kertomalla oikealta
![`<|>`(v[1],v[2])](images/harj6av29.gif) :n käänteismatriisilla.
:n käänteismatriisilla.
Warning, premature end of input
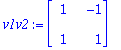
| > |
Lambda:=DiagonalMatrix([3,1/3]);
|
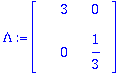
| > |
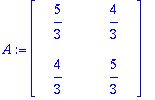
A:=v1v2.Lambda.v1v2^(-1);
|
| > |
Eigenvectors(A); #Tarkistus
|
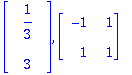
Luonnollinen kysmys: Jos tunnetaan matriisin ominaisarvot ja - vektorit, onko matriisi 1-käs. määrätty siinäkin tapauksessa, että se ei ole diagonalisoituva?
4.
| > |
v[1]:=<2,1,3>: v[2]:=<1,-2,0>; v[3]:=<6,3,-5>;
|
![v[2] := Vector(%id = 138851036)](images/harj6av34.gif)
![v[3] := Vector(%id = 135828288)](images/harj6av35.gif)
| > |
seq(seq(Sis(v[i],v[j]),j=1..3),i=1..3);linalg[matrix](3,3,[%]); # Tässä kohtuullisen kätevä tapa katsoa sisätulokombinaatiot.
|
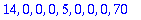
![matrix([[14, 0, 0], [0, 5, 0], [0, 0, 70]])](images/harj6av37.gif)
| > |
Matrix(3,3,(i,j)->Sis(v[i],v[j])); # Tässä on jo eleganssia, huomaa tämä matriisin muodostustapa!
|
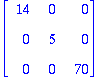
| > |
U:=<v[1]|v[2]|v[3]>; # Tämä on omalla tavallaan elegantein, pitää vaan osata ajatella "matriisiksi".
|
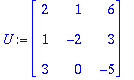
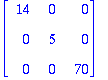
Jo se on varmaakin varmempaa!
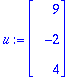
| > |
c[1]:=Sis(u,v[1])/Sis(v[1],v[1]);c[2]:=Sis(u,v[2])/Sis(v[2],v[2]);c[3]:=Sis(u,v[3])/Sis(v[3],v[3]);
|
![c[1] := 2](images/harj6av42.gif)
![c[2] := 13/5](images/harj6av43.gif)
![c[3] := 2/5](images/harj6av44.gif)
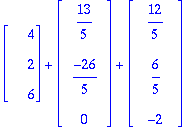
![vector([9, -2, 4])](images/harj6av46.gif)
Oikein meni!
5.
-
cos ja sin integroituna koko jakson yli = 0 , joten 1 on kohtisuorassa kaikkia muita vastaan.
-
| > |
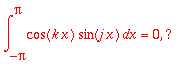 koska pariton kertaa parillinen on pariton , ja sellaisen int. yli O:n suht. symm. välin = 0.
koska pariton kertaa parillinen on pariton , ja sellaisen int. yli O:n suht. symm. välin = 0.
|
-
Jäljelle jäävät siten vain nämä:
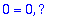
| > |
cos(x)*cos(2*x); %=combine(%);
|
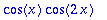
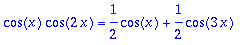
| > |
sin(x)*sin(2*x); %=combine(%);
|

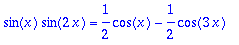
Ja taas integroidaan cos- tai sin- funkitota yhden tai useamman täyden jakson yli => 0.
Yleisesti:
| > |
cos(alpha*x)*cos(beta*x): %=combine(%);
|
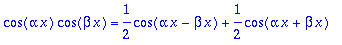
| > |
sin(alpha)*sin(beta): %=combine(%);
|
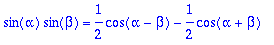
Emme siis tarvinneet Maplen erinomaista int-komentoa ollenkaan. No mikään ei estä:
| > |
F:=[1,cos(x),cos(2*x),sin(x),sin(2*x)];
|
![F := [1, cos(x), cos(2*x), sin(x), sin(2*x)]](images/harj6av55.gif)
| > |
Matrix(5,5,(i,j)->int(F[i]*F[j],x=-Pi..Pi));
|

Tätä on syytä ihastella!
6.
| > |
with(LinearAlgebra):alias(ref=GaussianElimination):
|
| > |
A:=<<3,1,-1,3>|<-5,1,5,-7>|<1,1,-2,8>>;
|
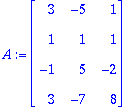
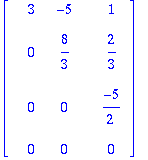
Ovat LRT, joten GS soveltuu. Tehdään vaiheittain "käsin laskien":
| > |
v:=seq(A[1..-1,j],j=1..3);
|
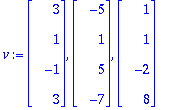
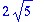
| > |
e[1]:=Normalize(v[1],2);
|
![e[1] := Vector(%id = 135616100)](images/harj6av61.gif)
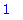
| > |
f[2]:=v[2]-Sis(v[2],e[1])*e[1];
|
![f[2] := Vector(%id = 135997900)](images/harj6av63.gif)
| > |
e[2]:=Normalize(f[2],2);
|
![e[2] := Vector(%id = 136076180)](images/harj6av64.gif)
| > |
f[3]:=v[3]-Sis(v[3],e[1])*e[1]-Sis(v[3],e[2])*e[2];
|
![f[3] := Vector(%id = 136351344)](images/harj6av65.gif)
| > |
e[3]:=Normalize(f[3],2);
|
![e[3] := Vector(%id = 136325956)](images/harj6av66.gif)

| > |
map(v->v*10/sqrt(5),[%]);
|
![[Vector(%id = 136480376), Vector(%id = 136555992), Vector(%id = 140515724)]](images/harj6av68.gif)
Tai:
| > |
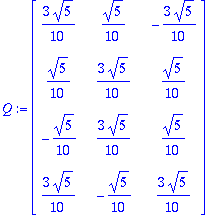
10*<e[1]|e[2]|e[3]>/sqrt(5);
|
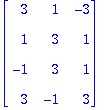
Valmiilla GramSchmidt:lla:
| > |
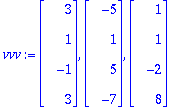
vvv:=seq(A[1..-1,j],j=1..3);
|
![[Vector(%id = 137406484), Vector(%id = 137395396), Vector(%id = 141093536)]](images/harj6av71.gif)
| > |
GramSchmidt([vvv],normalized);
|
![[Vector(%id = 141092736), Vector(%id = 137497476), Vector(%id = 141153800)]](images/harj6av72.gif)
![]()

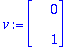
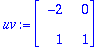
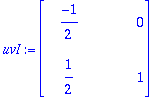
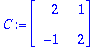
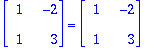
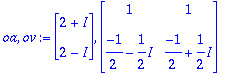
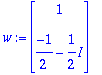
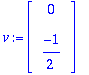
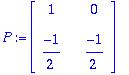
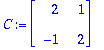
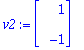
![x[k] = c[1]*3^k*Vector(%id = 140812236)+c[2]*(1/3)^k*Vector(%id = 138553320)](images/harj6av21.gif)
![[Maple Plot]](images/harj6av23.gif)
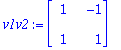
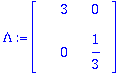

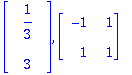
![v[2] := Vector(%id = 138851036)](images/harj6av34.gif)
![v[3] := Vector(%id = 135828288)](images/harj6av35.gif)
![matrix([[14, 0, 0], [0, 5, 0], [0, 0, 70]])](images/harj6av37.gif)

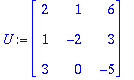

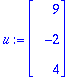

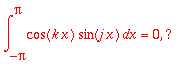 koska pariton kertaa parillinen on pariton , ja sellaisen int. yli O:n suht. symm. välin = 0.
koska pariton kertaa parillinen on pariton , ja sellaisen int. yli O:n suht. symm. välin = 0.




![e[1] := Vector(%id = 135616100)](images/harj6av61.gif)
![f[2] := Vector(%id = 135997900)](images/harj6av63.gif)
![e[2] := Vector(%id = 136076180)](images/harj6av64.gif)
![f[3] := Vector(%id = 136351344)](images/harj6av65.gif)
![e[3] := Vector(%id = 136325956)](images/harj6av66.gif)

![[Vector(%id = 136480376), Vector(%id = 136555992), Vector(%id = 140515724)]](images/harj6av68.gif)


![[Vector(%id = 137406484), Vector(%id = 137395396), Vector(%id = 141093536)]](images/harj6av71.gif)
![[Vector(%id = 141092736), Vector(%id = 137497476), Vector(%id = 141153800)]](images/harj6av72.gif)

