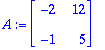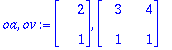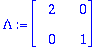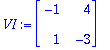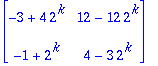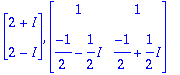1.
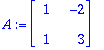
| > | A:=<<2,0,0>|<0,1,1>|<0,1,1>>; |
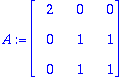
| > | M:=A-lambda*Id(3); |
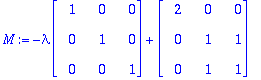
| > | p:=det(M); |
![]()
| > | factor(p); |
![]()
![]() ,
,
![]() ,
,
![]()
Ominaisvektorit:
Ominaiarvoa
![]() vastaava ominaisavaruus on sama kuin A:n nolla-avaruus N(A). Koska alg. kl =1, on geometrisen kl:n oltava myös 1.
vastaava ominaisavaruus on sama kuin A:n nolla-avaruus N(A). Koska alg. kl =1, on geometrisen kl:n oltava myös 1.
| > | ref(A); |
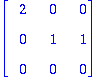
| > | x3:=t: x2:=-t: x1:=0: |
| > | v0:=subs(t=1,<x1,x2,x3>); # Tässä ominaisavaruuden kanta. |
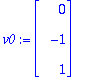
Kaksinkertaista ominaisarvoa
![]() vastaava ominaisavaruus:
vastaava ominaisavaruus:
| > | M2:=subs(lambda=2,M); |
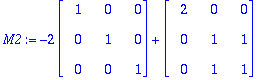
| > | ref(M2); |
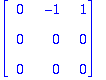
| > | x3:=s: x1:=t: x2:=x3: |
| > | v21:=subs(s=0,t=1,<x1,x2,x3>); |
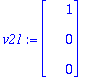
| > | v22:=subs(s=1,t=0,<x1,x2,x3>); |
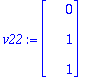
Tässä siis ominaisarvoon 2 liittyvän ominaisavaruuden kanta.
![]() ,
,
![]() .
.