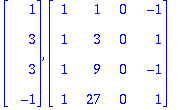
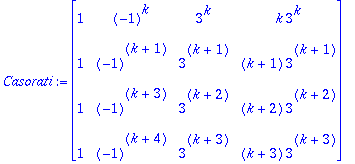Harj. 4 LV

pe 11.10.02

Alustukset

>    restart:with(LinearAlgebra):
with(linalg):
with(plots):setoptions(scaling=constrained):setoptions3d(axes=boxed,orientation=[-30,50]):

alias(Inv=MatrixInverse,Id=IdentityMatrix,Diag=DiagonalMatrix):
alias(rref=ReducedRowEchelonForm):alias(ref=GaussianElimination):
alias(Id=IdentityMatrix):
 

Warning, the name changecoords has been redefined



Warning, the previous binding of the name GramSchmidt has been removed and it now has an assigned value



Warning, the protected names norm and trace have been redefined and unprotected

1.

(a) Tehdään ensin 2 AV:

>    restart: 

Warning, the name changecoords has been redefined

>    EHY:=y(k+2)-a*(1+b)*y(k+1)+a*b*y(k)=1;

EHY := y(k+2)-a*(1+b)*y(k+1)+a*b*y(k) = 1

>    karyht:=r^2-a*(1+b)*r+a*b=0;

karyht := r^2-a*(1+b)*r+a*b = 0

>    r:=solve(karyht,r);

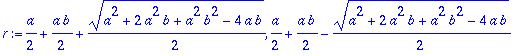
r := 1/2*a+1/2*a*b+1/2*(a^2+2*a^2*b+a^2*b^2-4*a*b)^(1/2), 1/2*a+1/2*a*b-1/2*(a^2+2*a^2*b+a^2*b^2-4*a*b)^(1/2)

>    r:=subs(a=0.9,b=4/9,[%]);

>   

r := [.8000000000, .5000000000]

>    Yh:=k->c1*r[1]^k + c2*r[2]^k;

Yh := proc (k) options operator, arrow; c1*r[1]^k+c2*r[2]^k end proc

>    yp:=k->T:  # yrite

>    EHYyr:=subs(y=yp,EHY);

EHYyr := yp(k+2)-a*(1+b)*yp(k+1)+a*b*yp(k) = 1

>    eval(EHYyr);

T-a*(1+b)*T+a*b*T = 1

>    Tarvo:=solve(%,T);

Tarvo := -1/(-1+a)

>    Yp:=k->Tarvo;

Yp := proc (k) options operator, arrow; Tarvo end proc

>    Yp(k);

-1/(-1+a)

>    a:=0.9;

a := .9

>    Yp(k);

.1e2

>    Y:=Yp+Yh;

Y := Yp+Yh

>    Y(k);

.1e2+c1*.8000000000^k+c2*.5000000000^k

Alkuarvot: Otetaan vaikka 1 ja 1 "bkt-yksikköä"..

>    c:=solve({Y(0)=1,Y(1)=1},{c1,c2});

c := {c2 = 6., c1 = -15.}

>    plot(subs(c,[seq([k,Y(k)],k=0..10)]));

[Maple Plot]

>    plot(subs(c,[seq([k,Y(k)],k=10..20)]));

[Maple Plot]

>    plot(subs(c,[seq([k,Y(k)],k=20..30)]));

[Maple Plot]

>    kuva1:=plot(subs(c,[seq([k,Y(k)],k=0..30)]),title="b=4/9",color=blue):

(B) Varsinainen alkuperäinen teht. 1 LV

>    a:='a': b:='b': y:='y':r:='r':

>    EHY:=y(k+2)-a*(1+b)*y(k+1)+a*b*y(k)=1;

EHY := y(k+2)-a*(1+b)*y(k+1)+a*b*y(k) = 1

>    karyht:=r^2-a*(1+b)*r+a*b=0;

karyht := r^2-a*(1+b)*r+a*b = 0

>    R:=solve(karyht,r);

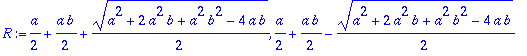
R := 1/2*a+1/2*a*b+1/2*(a^2+2*a^2*b+a^2*b^2-4*a*b)^(1/2), 1/2*a+1/2*a*b-1/2*(a^2+2*a^2*b+a^2*b^2-4*a*b)^(1/2)

>    R:=subs(a=0.9,b=0.5,[R]);

>   

>   

R := [.7500000000, .6000000000]

>    Yh:=k->c1*R[1]^k + c2*R[2]^k;

Yh := proc (k) options operator, arrow; c1*R[1]^k+c2*R[2]^k end proc

>    yp:=k->T:  # yrite

>    EHYyr:=subs(y=yp,EHY);

EHYyr := yp(k+2)-a*(1+b)*yp(k+1)+a*b*yp(k) = 1

>    eval(EHYyr);

T-a*(1+b)*T+a*b*T = 1

>    Tarvo:=solve(%,T);

Tarvo := -1/(-1+a)

>    Yp:=k->Tarvo;

Yp := proc (k) options operator, arrow; Tarvo end proc

>    Yp(k);

-1/(-1+a)

>    a:=0.9;

a := .9

>    Yp(k);

.1e2

>    Y:=Yp+Yh;

Y := Yp+Yh

>    Y(k);

.1e2+c1*.7500000000^k+c2*.6000000000^k

>    c:=solve({Y(0)=1,Y(1)=1},{c1,c2});

c := {c2 = 15., c1 = -24.}

>    plot(subs(c,[seq([k,Y(k)],k=0..10)]));

[Maple Plot]

>    plot(subs(c,[seq([k,Y(k)],k=10..20)]));

[Maple Plot]

>    kuva2:=plot(subs(c,[seq([k,Y(k)],k=0..30)]),title="b=0.5",color=red):

>    plots[display](kuva1,kuva2,title="AV ja LV teht 1");

[Maple Plot]

>    kuva1;

[Maple Plot]

Lisätehtävä 1 c)   b=5/9  (Lisäys annettu ma 7.10.)

>    a:='a': b:='b': y:='y':r:='r':

>    EHY:=y(k+2)-a*(1+b)*y(k+1)+a*b*y(k)=1;

EHY := y(k+2)-a*(1+b)*y(k+1)+a*b*y(k) = 1

>    karyht:=r^2-a*(1+b)*r+a*b=0;

karyht := r^2-a*(1+b)*r+a*b = 0

>    R:=solve(karyht,r);

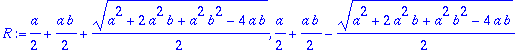
R := 1/2*a+1/2*a*b+1/2*(a^2+2*a^2*b+a^2*b^2-4*a*b)^(1/2), 1/2*a+1/2*a*b-1/2*(a^2+2*a^2*b+a^2*b^2-4*a*b)^(1/2)

>    R:=subs(a=0.9,b=5/9,[R]);

R := [.7000000000+.1000000000*I, .7000000000-.1000000000*I]

>   

Lisäys/muutos

>    yri:=k->a^k*cos(b*k);

yri := proc (k) options operator, arrow; a^k*cos(b*k) end proc

>    subs(y=yri,lhs(EHY));eval(%);

yri(k+2)-a*(1+b)*yri(k+1)+a*b*yri(k)

a^(k+2)*cos(b*(k+2))-a*(1+b)*a^(k+1)*cos(b*(k+1))+a*b*a^k*cos(b*k)

>    karakt:=simplify(%/a^k,symbolic);

karakt := a*(2*a*cos(b*k)*cos(b)^2-a*cos(b*k)-2*a*sin(b*k)*sin(b)*cos(b)-a*cos(b*k)*cos(b)+a*sin(b*k)*sin(b)-a*b*cos(b*k)*cos(b)+a*b*sin(b*k)*sin(b)+b*cos(b*k))
karakt := a*(2*a*cos(b*k)*cos(b)^2-a*cos(b*k)-2*a*sin(b*k)*sin(b)*cos(b)-a*cos(b*k)*cos(b)+a*sin(b*k)*sin(b)-a*b*cos(b*k)*cos(b)+a*b*sin(b*k)*sin(b)+b*cos(b*k))

>    karakt:=collect(%,cos(k*b));collect(%,sin(k*b));

karakt := a*(2*a*cos(b)^2-a-a*cos(b)-a*b*cos(b)+b)*cos(b*k)+a*(a*sin(b*k)*sin(b)-2*a*sin(b*k)*sin(b)*cos(b)+a*b*sin(b*k)*sin(b))
karakt := a*(2*a*cos(b)^2-a-a*cos(b)-a*b*cos(b)+b)*cos(b*k)+a*(a*sin(b*k)*sin(b)-2*a*sin(b*k)*sin(b)*cos(b)+a*b*sin(b*k)*sin(b))

a*(a*sin(b)-2*a*sin(b)*cos(b)+a*b*sin(b))*sin(b*k)+a*(2*a*cos(b)^2-a-a*cos(b)-a*b*cos(b)+b)*cos(b*k)

>    {coeff(karakt,cos(b*k),1)=0,coeff(karakt,sin(b*k),1)=0};

{a*(2*a*cos(b)^2-a-a*cos(b)-a*b*cos(b)+b) = 0, a*(a*sin(b)-2*a*sin(b)*cos(b)+a*b*sin(b)) = 0}

Eipä tuo aivan yksinkertainen yhtälö ole!

2.

>    with(LinearAlgebra): with(linalg): 

Warning, the previous binding of the name GramSchmidt has been removed and it now has an assigned value



Warning, the protected names norm and trace have been redefined and unprotected

>    A:=<<0,0,0,9>|<1,0,0,-6>|<0,1,0,-8>|<0,0,1,6>>;

A := Matrix(%id = 137372540)

>    X[0]:=<1,0,0,0>;

X[0] := Vector(%id = 137418308)

>    n:=20: for i to n do X[i]:=A.X[i-1] end do:

>    seq(X[i],i=0..10);

Vector(%id = 137418308), Vector(%id = 134933180), Vector(%id = 137577320), Vector(%id = 137601088), Vector(%id = 137627704), Vector(%id = 135100432), Vector(%id = 135287332), Vector(%id = 135608692), V...

b)

>    y[0]:=1: y[1]:=0: y[2]:=0: y[3]:=0:

>    n:=20: for k from 0 to n do
  y[k+4]:=6*y[k+3]-8*y[k+2]-6*y[k+1]+9*y[k]: end do:

>    seq(y[k],k=0..n);

1, 0, 0, 0, 9, 54, 252, 1026, 3897, 14148, 49824, 171612, 581265, 1943082, 6427116, 21074958, 68605713, 221959656, 714306528, 2288202264, 7300454841
1, 0, 0, 0, 9, 54, 252, 1026, 3897, 14148, 49824, 171612, 581265, 1943082, 6427116, 21074958, 68605713, 221959656, 714306528, 2288202264, 7300454841

>   

>    Eigenvectors(A);

Vector(%id = 137286720), Matrix(%id = 135094188)

>    eigenvectors(A);

[1, 1, {vector([1, 1, 1, 1])}], [-1, 1, {vector([-1, 1, -1, 1])}], [3, 2, {vector([1, 3, 9, 27])}]

>   

3.

>    restart: 

Warning, the name changecoords has been redefined

>    dyht:=y(k+4)-6*y(k+3)+8*y(k+2)+6*y(k+1)-9*y(k)=0;

dyht := y(k+4)-6*y(k+3)+8*y(k+2)+6*y(k+1)-9*y(k) = 0

>    karpol:=r^4-6*r^3+8*r^2+6*r-9;

karpol := r^4-6*r^3+8*r^2+6*r-9

>    factor(karpol);

(r-1)*(r+1)*(r-3)^2

>    yri:=k->k*3^k;

yri := proc (k) options operator, arrow; k*3^k end proc

>    yriy:=subs(y=yri,dyht);

yriy := yri(k+4)-6*yri(k+3)+8*yri(k+2)+6*yri(k+1)-9*yri(k) = 0

>    eval(yriy);

(k+4)*3^(k+4)-6*(k+3)*3^(k+3)+8*(k+2)*3^(k+2)+6*(k+1)*3^(k+1)-9*k*3^k = 0

>    expand(lhs(%));

0

Saadaan siis LRT ratlkaisut

>    y1:=k->1: y2:=k->(-1)^k: y3:=k->3^k: y4:=k->k*3^k:

Miten perustellaan LRT

>    Casorati:=<<y1(k),y1(k+1),y1(k+2),y1(k+3)>|<y2(k),y2(k+1),y2(k+3),y2(k+4)>|<y3(k),y3(k+1),y3(k+2),y3(k+3)>|<y4(k),y4(k+1),y4(k+2),y4(k+3)>>;

Casorati := Matrix(%id = 137967492)

>    linalg[det](Casorati);

(-1)^(k+1)*3^(k+2)*3^(k+3)-2*(-1)^(k+3)*3^(k+1)*3^(k+3)+(-1)^(k+4)*3^(k+1)*3^(k+2)-(-1)^k*3^(k+2)*3^(k+3)+3*(-1)^(k+3)*3^k*3^(k+3)-2*(-1)^(k+4)*3^k*3^(k+2)+2*(-1)^k*3^(k+1)*3^(k+3)-3*(-1)^(k+1)*3^k*3^(...
(-1)^(k+1)*3^(k+2)*3^(k+3)-2*(-1)^(k+3)*3^(k+1)*3^(k+3)+(-1)^(k+4)*3^(k+1)*3^(k+2)-(-1)^k*3^(k+2)*3^(k+3)+3*(-1)^(k+3)*3^k*3^(k+3)-2*(-1)^(k+4)*3^k*3^(k+2)+2*(-1)^k*3^(k+1)*3^(k+3)-3*(-1)^(k+1)*3^k*3^(...
(-1)^(k+1)*3^(k+2)*3^(k+3)-2*(-1)^(k+3)*3^(k+1)*3^(k+3)+(-1)^(k+4)*3^(k+1)*3^(k+2)-(-1)^k*3^(k+2)*3^(k+3)+3*(-1)^(k+3)*3^k*3^(k+3)-2*(-1)^(k+4)*3^k*3^(k+2)+2*(-1)^k*3^(k+1)*3^(k+3)-3*(-1)^(k+1)*3^k*3^(...
(-1)^(k+1)*3^(k+2)*3^(k+3)-2*(-1)^(k+3)*3^(k+1)*3^(k+3)+(-1)^(k+4)*3^(k+1)*3^(k+2)-(-1)^k*3^(k+2)*3^(k+3)+3*(-1)^(k+3)*3^k*3^(k+3)-2*(-1)^(k+4)*3^k*3^(k+2)+2*(-1)^k*3^(k+1)*3^(k+3)-3*(-1)^(k+1)*3^k*3^(...

>    simplify(%);

192*(-1)^(k+1)*9^k

>   

>   

>