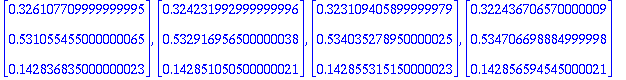1.
| > | with(plots): |
| > | Lka:=y->seq((y[k-1]+y[k]+y[k+1])/3,k=2..nops(y)-1); |
![]()
| > | y:=[9,5,7,3,2,4,6,5,7,6,8,10,9,5,7]; |
![]()
| > | z:=[Lka(y)]; |
![]()
| > |
| > | ykuva:=plot([seq([k,y[k]],k=1..nops(y))],color=blue): |
| > | yrinkulat:=plot([seq([k,y[k]],k=1..nops(y))],style=point,symbol=circle,symbolsize=18,color=blue): |
| > | zkuva:=plot([seq([k+1,z[k]],k=1..nops(z))],color=red): |
| > | zrinkulat:=plot([seq([k+1,z[k]],k=1..nops(z))],style=point,symbol=circle,symbolsize=15,color=red): |
| > | display(ykuva,yrinkulat,zkuva,zrinkulat); |
![[Maple Plot]](images/harj4av4.gif)
| > | display(array([[ykuva],[zkuva]])); |
![[Maple Plot]](images/harj4av5.gif)
| > |
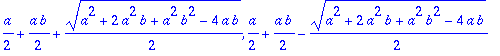
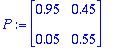
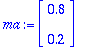
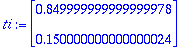
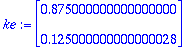
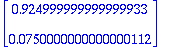

![X[0] := Vector(%id = 134651332)](images/harj4av16.gif)