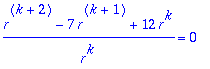1.
| > | cos(2*t): %=expand(%); cos(3*t): %=expand(%); cos(4*t): %=expand(%); cos(5*t): %=expand(%); cos(6*t): %=expand(%); |
![]()
![]()
![]()
![]()
![]()
| > | B:=[x[0]=1,seq(x[k]=cos(t)^k,k=1..6)]; |
![]()
| > | C:=[y[0]=1,seq(y[k]=cos(k*t),k=1..6)]; |
![]()
B:n LRT:
Merk. s=cos(t), jolloin B:n funktiot ovat s:n monomeja välillä [-1,1]. Nehän nyt taatusti tiedetään LRT:ksi, joten
yhtälöstä
| > | sum(c[k]*cos(t)^k,k=0..6)=0; |
![]()
seuraa
| > | sum(c[k]*s^k,k=0..6)=0; |
![]()
kaikilla s välillä [-1,1], joten
| > | seq(c[k]=0,k=0..6); |
![]()
C on kanta:
Koska B on kanta, niin kuvaus
| > | f->[f][B]; |
![]()
on isomorfismi. Kuvauksessa LRT siten säilyy, joten riittää osoittaa, että koordinaattivektorit
| > | seq([y[k]]['B'],k=0..6); |
![]()
ovat LRT.
| > | S:=<<1,0,0,0,0,0,0>|<0,1,0,0,0,0,0>|<-1,0,2,0,0,0,0>|<0,-3,0,4,0,0,0>|<1,0,-8,0,8,0,0>|<0,5,0,-20,0,16,0>|<-1,0,18,0,-48,0,32>>; |

Tälle ei tarvitse tarjoilla ref:fiä, sillä se on jo valmiiksi ref-muodossa.
Kaikki sarakkeet pivot-sarakkeita, joten S:n sarakkeet ovat LRT ja siten siis myös
![]() - vektorit.
- vektorit.
Tässä tehtävässä ei Maplea tarvittu mitenkään olennaisesti (paitsi trig. kaavojen generoimiseen ja matemaattiseen tekstinkäsittelyyn).
Kynä/paperi ja taulukkokirja olisivat toimineet myös aivan hyvin.

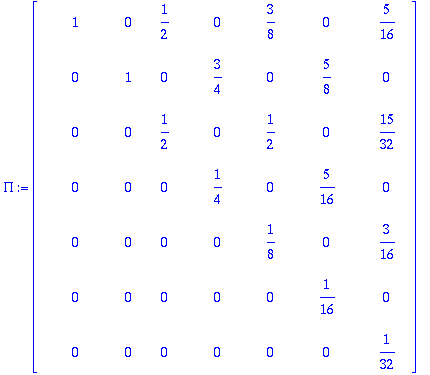
 :llä.
:llä.
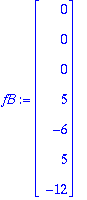
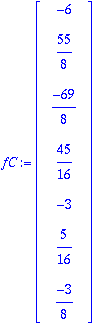
![[Maple Plot]](images/harj3lv38.gif)
![matrix([[0, 10000], [1, 9650.00], [2, 9296.5000], [3, 8939.465000], [4, 8578.859650], [5, 8214.648246], [6, 7846.794728], [7, 7475.262675], [8, 7100.015302], [9, 6721.015455], [10, 6338.225610], [11, 5...](images/harj3lv39.gif)