Alustukset

>	restart:with(linalg): with(LinearAlgebra): alias(rref=ReducedRowEchelonForm): alias(ref=GaussianElimination):  # "row echelon form"

Warning, the name changecoords has been redefined

Warning, the protected names norm and trace have been redefined and unprotected

Warning, the assigned name GramSchmidt now has a global binding

>

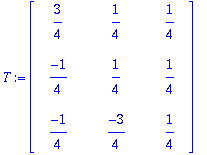
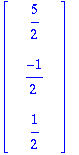
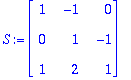1.

Olkoon

>	x:=c[1]*f[1]+c[2]*f[1]+c[3]*f[3];

Sijoitetaan tähän F-kantavektorien lausekkeet D-vektorin avulla ja kerätään D-vektorien kertoimet yhteen.

(Mitään muuta "teoriaa" koko hommassa ei olekaan.)

 =>

>	S:=<<2,-1,1>|<0,3,1>|<-3,0,2>>;

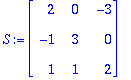
Tarkista vielä, että matriisin sarakkeet ovat vektorit

>	seq([f[j]][D],j=1..3);

b)

>	S.<1,-2,2>;

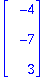
c)  (Tällainen olisi kannattanut laittaa, mutta tällä kertaa tuli turhan vähän a)-b)-c)-kohtia :-) )

     Annettu vektori F-kannassa (uudessa kannassa), esitä se vanhassa D-kannassa.

>	vD:=<1,2,3>;

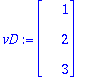
>	vF:=LinearSolve(S,vD);

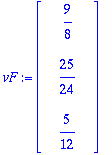
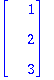
>	S.vF;  # Tarkistus

Tässä on oikeastaan kaikki mahdolliset tehtävätyypit, joita kannanvaihdossa voi esiintyä.

"Teoriasta" on syytä muistaa:

•  Jos vanhat kantavektorit  annetaan uusien avulla  matriisilla S^T (transpoosi), niin vektorin
•   uudet koordinaatit  saadaan vanhoista koordinaateista  kertomalla matriisilla S.
• Siis jos on annettu "uudet vanhoissa"  ja on laskettava "uudet vanhoissa" , täytyy ratkaista lineaarinen   yhtälösysteemi.

2.

3.

>	restart:with(linalg): with(LinearAlgebra):

Warning, the name changecoords has been redefined

Warning, the protected names norm and trace have been redefined and unprotected

Warning, the assigned name GramSchmidt now has a global binding

>	S:=<<1,0,1>|<-1,1,2>|<0,-1,1>>;

>	T:=MatrixInverse(S);

>	T.<3,-1,2>;

>	q1:=x^2+1: q2:=2*x^2+x-1: q3:=x^2-x:

>	5/2*q1-1/2*q2+1/2*q3;

>

>