Harj. 2 LV
pe 27.9.02 HA
Alustukset
| > |
restart:with(linalg):
with(LinearAlgebra):
alias(rref=ReducedRowEchelonForm):alias(ref=GaussianElimination): # "row echelon form"
|
Warning, the name changecoords has been redefined
Warning, the protected names norm and trace have been redefined and unprotected
Warning, the assigned name GramSchmidt now has a global binding
| > |
# A:=<<>|<>|<>|<>|<>>; # Leikkaa/liimaa/modifioi!
|
1.
Maple-tekniikkaa: Kannattaa ensin lopettaa puolipisteeseen, jotta on helppo tarkistaa. Sitten editoidaan puolipisteet kaksoispisteiksi, jotta liika tulostus ei häiritse.
| > |
v1:=<1,1,0,0,1>:v2:=<0,2,0,1,-1>:v3:=<0,-1,1,0,2>: v4:=<1,4,1,2,1>: v5:=<0,0,2,1,3>:
|
Osaamme lukea tuloksen suoraan ref:n avulla muodostamalla matriisin sarakeavaruuden kannan. Tehdään tässä kuitenkin perusteista lähtien.
Koska jokainen virittävä joukko voidaan karsia kannaksi, lähdetään liikkeelle koko vektorijoukosta ja katsotaan olisiko se LRT, jolloin se olisi kanta.
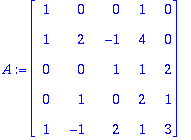

Tästä nähdään, että 2 viimeistä voidaan lausua 3:n ensimmäisen lineaarikombinaationa ja 3 ekaa ovat LRT. Siis {v1,v2,v3} on ko. kanta.
Huomaa! Tämä voidaan ajatella niin, että 3 ekaa saraketta ovat kerroinmatriisi ja 2 vikaa ovat "b-vektoreita".
rref(A)
:sta näkyy jopa lineaarikombinaatioiden
kertoimet
kannassa {v1,v2,v3}.
v4:n tapauksessa [1,2,1] ja v5:n tapauksessa [0,1,2].
Toki voidaan kirjoittaa v-vektorit eri järjestykseen, vaikkapa:
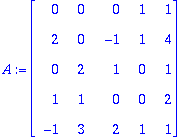

Kannaksi kelpaa siis {v2,v5,v1} (miltei mikä tahansa kolmikko, paitsi esim. {v2,v5,v3}. )
Ehkä tuo loppuosa ei ole erikoisen kehittävä. Tietysti mikä tahansa 3:n LRT vektorin (tai 3:n virittävän vektorin joukko kelpaa, kun kerran dim=3.
2.
| > |
restart:with(linalg):
with(LinearAlgebra):
alias(rref=ReducedRowEchelonForm):alias(ref=GaussianElimination):
|
Warning, the name changecoords has been redefined
Warning, the protected names norm and trace have been redefined and unprotected
Warning, the assigned name GramSchmidt now has a global binding
| > |
A:=<<5,3,8,2>|<1,3,4,1>|<2,2,4,1>|<2,-1,-5,0>|<0,-12,12,-2>>;
|

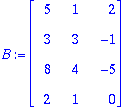
| > |
Ba3a5:=<B|A[1..-1,[3,5]]>;
|
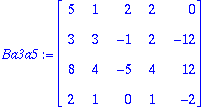

Kaksi viimeistä saraketta antavat jopa lineaarikombinaatioiden kertoimet (kuullostaako tutulta?).
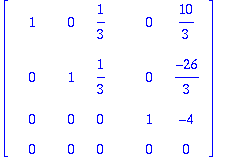
Tästä ratkaistaan käsin =>
| > |
v1:=<-1,-1,3,0,0>;v2:=<-10,26,0,12,3>;
|
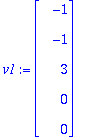
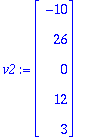
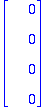
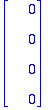
Siis oikein laskettu, ja selvästi ovat LRT (toisessa 0 sellaisella kohdalla, jossa toisessa #0 ja kääntäen).
Kokeillaan, mitä LinearSolve antaa.
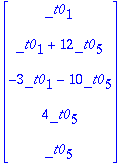
Tästä luetaan kantavektorit:
| > |
w1:=<1,1,-3,0,0>;w2:=<0,12,-10,4,1>;
|
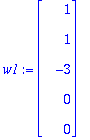
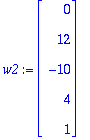
Erilaiselta näyttää, mutta ovat LRT, katsotaan kuuluvatko ytimeen, sehän riittää..
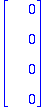
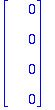
Kyllä vaan!
Paljastetaanpa lopuksi myös tämä: Saadaan näköjään sama tulos, jonka LinearSolve antaa.
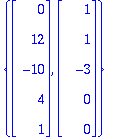
c) Koska N(A):ssa on nollasta erillisiä vektoreita (jopa dim=2), niin ei voi olla injektio.
Koska R(LA) on A:n sarakeavaruus, ja se on 3-ulotteinen, eivät kuvat voi täyttää 4-ulotteista avaruutta.
Voidaan tietysti laskea LA:n peruslauseen (dimensiolauseen) mukaan: n(A)+r(A)=5 . Johtopäätöksen tekoon riittäisi
siten tietää vain toinen, n(A) tai r(A), mutta laskimme nyt kaiken mahdollisen.
3.
| > |
A:=<<1,2,3>|<3,1,4>|<-1,5,4>|<4,7,11>>;
|
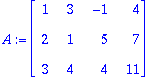
Sarakeavaruus:
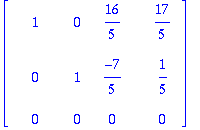
Kaksi ensimmäistä A:n saraketta ovat LRT, kaksi jälkimmäistä saadaan lineearikombinaatioina (kertoimet ovat tässä rref(A)-
matriisissa.)
| > |
sarakekanta:=A[1..-1,1..2];
|
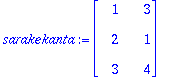
Jos halutaan, ettei lukijan tarvitse mielessään irrotella matriisin sarakkeita, voidaan kirjoittaa:
| > |
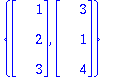
{A[1..-1,1],A[1..-1,2]};
|
![[Vector(%id = 138509112), Vector(%id = 136436348)]](images/harj2lv24.gif)
Maple määrittää sarakeavaruuden kannan ottamatta kantavektoreita sarekkeiden joukosta. (Hyväksyttävää toki,
niinhän mekin teemme riviavaruuden kohdalla (ainakin se on toinen perustapa)).
Riviavaruus:
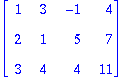
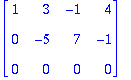
| > |
rivikanta:=%[1..2,1..-1];
|
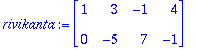
| > |
rivikanta:=Transpose(rivikanta);
|
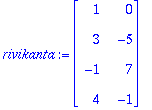
| > |
{rivikanta[1..-1,1],rivikanta[1..-1,2]};
|
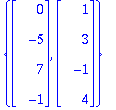
Voidaan myös muodostaa A^T:n sarakekantana:
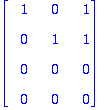
Tästä nähdään, että A:n kaksi ekaa riviä muodostavat riviavaruuden kannan.
Huom!
Yleisesti riviavaruuden kantaa ei saada valitsemalla A:sta samoja rivejä kuin rref(A):n nollasta erilliset.
Lukumäärä on kyllä oikea, mutta rivioperaatioissa rivien paikat saattavat muuttua. Viritys säilyy kumpaankin suuntaan,
mutta myöskään LRV/LRT-käytös ei välttämättä lineaarikombinaatioita muodostamalla säily.
![[Vector(%id = 136007352), Vector(%id = 136007392)]](images/harj2lv31.gif)
4.
Warning, the name changecoords has been redefined
a) Kynä+paperi/liitu+taulu
b) A on (mxn) , A^T on (nxm). Sovelletaan dimensiolausetta A^T-matriisiin:
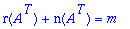
Mutta
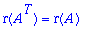
5.
a)
| > |
sum(c[k]*x^k,k=0..n)=0;
|
![sum(c[k]*x^k,k = 0 .. n) = 0](images/harj2lv34.gif)
Sijoitetaan x=0 => c0=0
Yo. yhtälöstä seuraa myös, että D(p)=0. Derivoidaan ja sijoitetaan x=0 => c1 = 0.
Näin jatketaan, kunnes jäljellä on 1. asteen polynomi, sen derivaatta on myös = 0 => cn = 0.
Tämä toimii, kun 0 kuuluu määrittelyjoukkoon. Ellei, voidaan tehdä muuttujanvaihto x=y+c, missä c kuuluu
määrittelyjoukkoon. Sovelletaan samaa päättelyä y:n polynomiin, jolla 0 on määrittelyjoukossa.
b) on selitetty tehtäväpaperissa
c) Määrittelyjoukko [a,b]
| > |
sum(c[k]*x^k,k=0..n)=0;
|
![sum(c[k]*x^k,k = 0 .. n) = 0](images/harj2lv35.gif)
Siis polynomi saa arvon nolla erillisissä välin pisteissä x0 < x1 < ... < xn.
Mutta tällöin polynomi voidaan kirjoittaa tuloksi:
| > |
product(c[n]*(x-x[k]),k=0..n-1);
|
![product(c[n]*(x-x[k]),k = 0 .. n-1)](images/harj2lv36.gif)
Koska tämä tulo = 0 myös pisteessä xn, on oltava cn = 0,
Tehdään sama päätelmä jäljellä olevaan (n-1)-asteiseen polynomiin => c[n-1] = 0 ... c[0] = 0.
Huom! Tässäkään ei tarvita mitään syvällistä, kuten algebran peruslausetta. Oletuksenahan on, että 0-kohtia
riittää. Se, että jos polynomilla on 0-kohta c,niin se on jaollinen (x - c):llä, on helppo juttu (lukion asioita).
Ehkä unohdetaan Vandermonde- asiat tällä kertaa. Piirretään kuitenkin pari monomikuvaa.
| > |
plot([seq(x^k,k=10..15)],x=-1..1);
|
![[Maple Plot]](images/harj2lv37.gif)
| > |
plot([seq(x^k,k=[10,12,14])],x=-1..1);
|
![[Maple Plot]](images/harj2lv38.gif)
6.
| > |
restart:restart:with(linalg):
with(LinearAlgebra):
|
Warning, the name changecoords has been redefined
Warning, the name changecoords has been redefined
Warning, the protected names norm and trace have been redefined and unprotected
Warning, the assigned name GramSchmidt now has a global binding
| > |
N:=<<<0|0.5|0.5|6|6|5.5|5.5|0>,<0|0|6.42|0|8|8|1.58|8>>|<0,0>>;
|
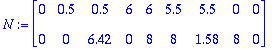
Rakennettiin vaihteeksi riveittäin, mutta lisättiin lopuksi vielä alkupiste, jotta kuvio sulkeutuisi.
| > |
convert(Transpose(N),listlist); # Kätevää!
|
![[[0, 0], [.5, 0], [.5, 6.42], [6, 0], [6, 8], [5.5, 8], [5.5, 1.58], [0, 8], [0, 0]]](images/harj2lv40.gif)
Näissä kannattaa valita akseleille sama skaala ("scaling=constrained")
| > |
plot(%,scaling=constrained);
|
![[Maple Plot]](images/harj2lv41.gif)
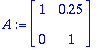
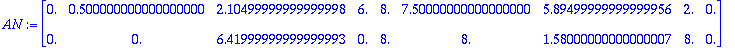
| > |
plot(convert(Transpose(AN),listlist),scaling=constrained);
|
![[Maple Plot]](images/harj2lv44.gif)
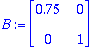
| > |
B.<<x,y>>;
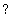
|
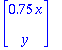
| > |
plot(convert(Transpose(B.AN),listlist),scaling=constrained);
|
![[Maple Plot]](images/harj2lv48.gif)
Kiertomatriisi:
Kun tason pisteitä kierretään kulmalla
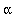
niin kantavektorien kuvat ovat C-matriisin sarakkeet.
| > |
C:=<<cos(alpha),sin(alpha)>|<-sin(alpha),cos(alpha)>>;
|
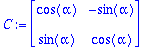
| > |
plot(convert(Transpose(C.B.AN),listlist),scaling=constrained);
|
![[Maple Plot]](images/harj2lv51.gif)
| > |
plot(convert(Transpose(C.C.B.AN),listlist));
|
![[Maple Plot]](images/harj2lv52.gif)
Siirto jätetään omaehtoiseen harrastukseen.









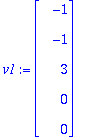
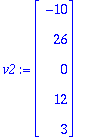


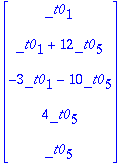
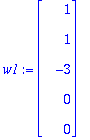
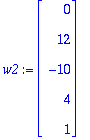



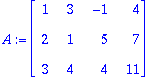

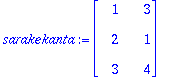

![[Vector(%id = 138509112), Vector(%id = 136436348)]](images/harj2lv24.gif)
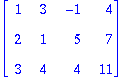
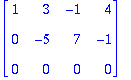
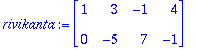
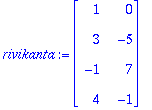


![sum(c[k]*x^k,k = 0 .. n) = 0](images/harj2lv34.gif)
![sum(c[k]*x^k,k = 0 .. n) = 0](images/harj2lv35.gif)
![product(c[n]*(x-x[k]),k = 0 .. n-1)](images/harj2lv36.gif)
![[Maple Plot]](images/harj2lv37.gif)
![[Maple Plot]](images/harj2lv38.gif)
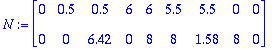
![[Maple Plot]](images/harj2lv41.gif)
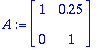
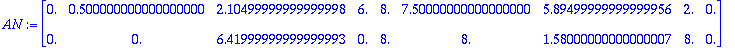
![[Maple Plot]](images/harj2lv44.gif)
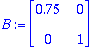
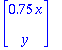
![[Maple Plot]](images/harj2lv48.gif)
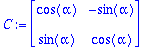
![[Maple Plot]](images/harj2lv51.gif)
![[Maple Plot]](images/harj2lv52.gif)