Harj. 1 LV
pe 20.9.02 HA
Alustukset
| > |
restart:with(linalg):
with(LinearAlgebra):
alias(rref=ReducedRowEchelonForm):alias(ref=GaussianElimination): # "row echelon form"
|
Warning, the name changecoords has been redefined
Warning, the protected names norm and trace have been redefined and unprotected
Warning, the assigned name GramSchmidt now has a global binding
| > |
Reshape:=(vek,m,n)->Matrix(linalg[matrix](m,n,convert(vek,list)));
|
)) end proc](images/harj1lv1.gif)
1.
Pidetään tunnettuna, että mxn-matriisit muodostavat vektoriavaruuden. Itse asiassa matriisiavaruus "on sama kuin" R^(mn), samahan se on kaikkien
VA-laskusääntöjen kannalta, ajatellaanko oliot pitkinä vektoreina vai "Reshape:lla" muotoilluina matriiseina. Kaikkihan tapahtuu vastinalkioittain.
Aliavaruudeksi osoittaminen on vain sitä, että summan täytyy kuulua ja skalaari kertaa olion täytyy kuulua ao. aliavaruuskandidaattiin.
On tietysti syytä todeta, että AA-kandidaatti ei ole tyhjä. Luonnollisin tarkistus sille, on todeta, että 0-alkio kuuluu siihen.
No tässä tapauksessa näin on ilman muuta. (Yläkolmiomatriisihan tarkoittaa, että alakolmio on nolla, muu osa saa olla mitä tahansa.)
| > |
A1:=<<a1,0>|<b1,d1>>;A2:=<<a2,0>|<b2,d2>>;
|
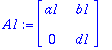
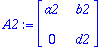
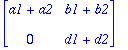
Siis kahden yläkolmiomatriisin summa on yläkolmiomatriisi.
| > |
evalm(c*A1); # evalm "kertoo skalaarin sisään"
|
![matrix([[c*a1, c*b1], [0, c*d1]])](images/harj1lv5.gif)
Niinpä joukkomme on suljettu myös skalaarilla kertomisen suhteen, ja kaikki on kunnossa.
Huom 1: Tässä ei todellakaan Maplea tarvittu muuta kuin tekstinkäsittelyyn. Sinänsä on hyvä huomata, että Maplea voi käyttää hyvin ihan vaan
matemaattisen dokumentin tuottamiseen, senhänsaa muunnetuksi myös html-muotoon.
Huom2: Tietystikään 2x2 ei ole mikään maaginen koko, vaan päättely toimii minkäkokoiselle tahansa.
2.
Uusi tehtävä on syytä aloittaa restartilla. Sen jälkeen pitää ladata arpeelliset kirjatot, määritellä aliakset jne.
| > |
restart:with(linalg):
with(LinearAlgebra):
alias(rref=ReducedRowEchelonForm):alias(ref=GaussianElimination):
|
Warning, the name changecoords has been redefined
Warning, the protected names norm and trace have been redefined and unprotected
Warning, the assigned name GramSchmidt now has a global binding
| > |
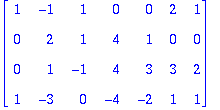
A:=<<1,1,-1,1>|<-1,1,2,-3>|<1,2,-2,0>|<0,4,4,-4>|<0,1,3,-2>|<2,2,1,1>>;
|


Kts. rivioperaatioissa mallia
LA.mws
:stä
| > |
Ab[2,1..-1]:=Ab[2,1..-1]-Ab[1,1..-1]: Ab;
|

| > |
Ab[3,1..-1]:=Ab[3,1..-1]+Ab[1,1..-1]: Ab;
|

| > |
Ab[4,1..-1]:=Ab[4,1..-1]-Ab[1,1..-1]: Ab;
|

1. sarake nollattu. Siirrytään 2. sarakkeeseen.
| > |
Ab[3,1..-1]:=Ab[3,1..-1]-Ab[2,1..-1]/2:
|
| > |
Ab[4,1..-1]:=Ab[4,1..-1]+Ab[2,1..-1]: Ab;
|

2. sarake nollattu. Tässä tuli ref-muoto valmiiksi. Tukisarakkeet: 1,2,3,5.
1 vapaa parametri.
Kannattaa harjoitella myös ratkaismista "käsin" takaisinsijoituksella LA.mws-mallin mukaan.
Huom! Jos jokin rivioperaatio menee väärin, on aloitettava alusta, siis riviltä A:=...
3.
| > |
restart: with(linalg): with(LinearAlgebra): with(plots):Reshape:=(vek,m,n)->Matrix(linalg[matrix](m,n,convert(vek,list)));
|
Warning, the name changecoords has been redefined
Warning, the protected names norm and trace have been redefined and unprotected
Warning, the assigned name GramSchmidt now has a global binding
)) end proc](images/harj1lv14.gif)
| > |
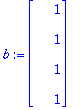
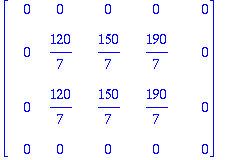
A:=<<4,-1,0,-1,0,0>|<-1,4,-1,0,-1,0>|<0,-1,4,0,0,-1>|<-1,0,0,4,-1,0>|<0,-1,0,-1,4,-1>|<0,0,-1,0,-1,4>>;
b:=<30,20,60,30,20,60>;
|

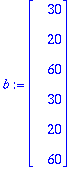
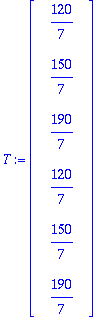

| > |
vaaka:=<15|20|20|20|30>;
vasen:=<10,10>;
oikea:=<40,40>;
|
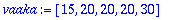
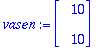
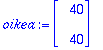
| > |
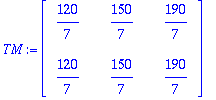
TT[4,1..-1]:=vaaka:
TT;
|

| > |
TT[2..3,1]:=vasen:
TT[2..3,5]:=oikea:
TT;
|

| > |
matrixplot(TT,axes=boxed);
|
![[Maple Plot]](images/harj1lv26.gif)
4.
| > |
restart: with(linalg): with(LinearAlgebra): alias(ref=GaussianElimination):alias(rref=ReducedRowEchelonForm):
|
Warning, the name changecoords has been redefined
Warning, the protected names norm and trace have been redefined and unprotected
Warning, the assigned name GramSchmidt now has a global binding
Käsin laskien saadaan matriisi B:
| > |
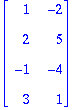
B:=<<1,2,-1,3>|<-2,5,-4,1>|<5,-8,7,1>>;rref(B);
|
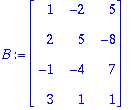
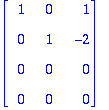
Vektorit ovat LRV, kaksi ensimmäistä ovat LRT ja virittävät saman, joten ne muodostavat kannan.
Harjoitellaan vielä osamatriisia ja todetaan erikseen kahden ekan LRT (vaikka se tuleekin jo edellisellä laskulla.)
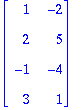
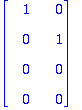
| > |
B[1..4,1..2]; # Tietysti voidaan tässä ottaa 1..2 yhtä helposti kuin 1..-2. Jälkimmäinen yleisempi.
|
![]()
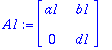
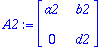
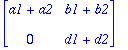
![matrix([[c*a1, c*b1], [0, c*d1]])](images/harj1lv5.gif)









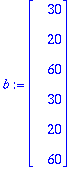



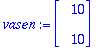
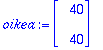


![[Maple Plot]](images/harj1lv26.gif)




