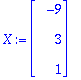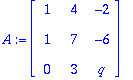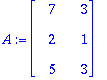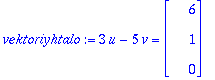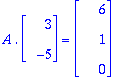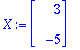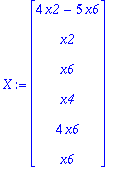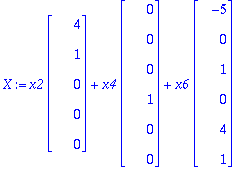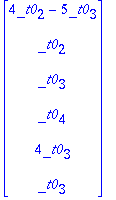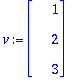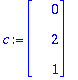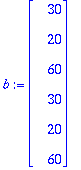V3/s02 Harj1av ratkaisuja

H/ratk/harj1av.mws    HA syyskuu 02 

Warning, the name changecoords has been redefined

Alustukset

>    restart:with(linalg):
with(LinearAlgebra):
alias(rref=ReducedRowEchelonForm):
alias(ref=GaussianElimination):  # "row echelon form"
 

Warning, the name changecoords has been redefined



Warning, the protected names norm and trace have been redefined and unprotected



Warning, the assigned name GramSchmidt now has a global binding

>   

1.

>    Ab:=<<1,1,0>|<4,7,3>|<-2,-6,q>|<1,6,t>>;

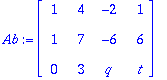
Ab := Matrix(%id = 135060588)

>    E:=ref(Ab);

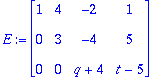
E := Matrix(%id = 135399136)

  q=-4 on singulaarisuusehto. Tällöin:

>    E:=subs(q=-4,E);

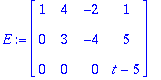
E := Matrix(%id = 135397820)

Ratkaisuja on joss  t=5.

>    E:=subs(t=5,E);

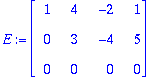
E := Matrix(%id = 135384656)

>    rref(%);

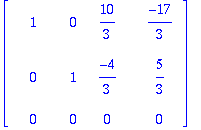
Matrix(%id = 136048028)

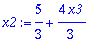
>    x2:=5/3+4/3*x3;

x2 := 5/3+4/3*x3

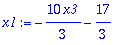
>    x1:=-10/3*x3-17/3;

x1 := -10/3*x3-17/3

>    X:=Vector([subs(x3=1,x1),subs(x3=1,x2),subs(x3=1,x3)]);

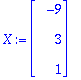
X := Vector(%id = 134825396)

>    A:=Ab[1..-1,1..-2];

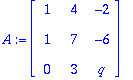
A := Matrix(%id = 135471836)

Tarkistus:

>    subs(q=-4,A).X;

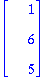
Vector(%id = 134833292)

Kyllä toteutuu!

2.

>    u:=<7,2,5>: v:=<3,1,3>: w:=<6,1,0>:

>    3*u-5*v-w;

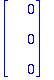
Vector(%id = 134814612)

Toteutuu.

>    A:=<u | v>;

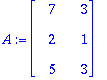
A := Matrix(%id = 138376660)

Kun sarakeajattelu muutetaan riviajatteluksi (vektoriyhtälö matriisiyhtälöksi), niin:

>    vektoriyhtalo:='3*u-5*v'=w;

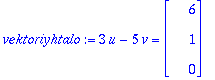
vektoriyhtalo := 3*u-5*v = Vector(%id = 134833864)

Muutetaan vektoriyhtälö matriisiyhtälöksi (sarakeajattelu riviajatteluksi):

>    'A' . <3,-5> = w;

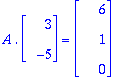
A.Vector(%id = 134763980) = Vector(%id = 134833864)

Estettiin matriisitulon laseknta vasemmalla, jotta saadaan järkevännäköinen yhtälö. Siis ratkaisu:

>    X:=<3,-5>;

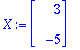
X := Vector(%id = 134784960)

3.

Ab, Bb, Cb ovat ref-muodossa.

Ab: 2 ensimmäistä ovat pivot-sarakkeita. Yksi vapaa muuttuja (eli vapaa parametri).

Bb Ristiriitainen yhtälö 0 = 2, ei ratkaisuja.

Cb: Kaikki kerroinmatriisisarakkeet ovat tuki(pivot-)sarakkeita => 1-käs. ratkaisu.

>    Db:=<<1,2,0,0>|<0,3,3,0>|<2,6,2,0>|<0,1,1,0>|<3,16,10,0>>;

Db := Matrix(%id = 140042312)

>    ref(Db);

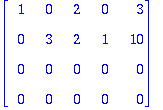
Matrix(%id = 140701812)

2. ensimmäistä saraketta ovat tukisarakkeita. 2 vapaata parametria.

4.

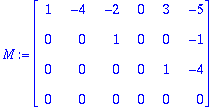
>    M:=<<1,0,0,0>|<-4,0,0,0>|<-2,1,0,0>|<0,0,0,0>|<3,0,1,0>|<-5,-1,-4,0>>;

M := Matrix(%id = 137237552)

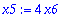
>    x5:=4*x6;

x5 := 4*x6

>    x3:=x6;

x3 := x6

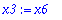
>    x1:=4*x2+2*x3-3*x5+5*x6;

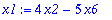
x1 := 4*x2-5*x6

>    X:=<x1,x2,x3,x4,x5,x6>;

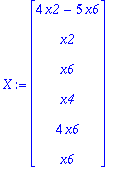
X := Vector(%id = 135945880)

>    M.X;

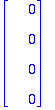
Vector(%id = 138616636)

Esitetään vektorien lineaarikombinaationa:

>    X:=x2*<4,1,0,0,0>+x4*<0,0,0,1,0,0>+x6*<-5,0,1,0,4,1>;

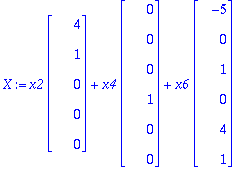
X := x2*Vector(%id = 138616676)+x4*Vector(%id = 138616716)+x6*Vector(%id = 138616796)

Tarkistetaan vielä:

>    LinearSolve(M,<0,0,0,0>);

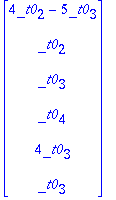
Vector(%id = 138616876)

>   

5.

>    v1:=<1,1,0>: v2:=<0,1,1>: v3:=<1,0,1>:

>    A:=<v1|v2|v3>;

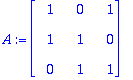
A := Matrix(%id = 135802168)

>    ref(A);

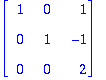
Matrix(%id = 135170776)

Kaikki sarakkeet ovat PIVOT-sarakkeita, joten HY:llä vain 0-ratkaisu ==> LRT.

Sama ehto on välttämätön ja riittävä sille, että vektorit virittävät koko R^3:n. (Vastakkaisessa tapauksessa ref:ssä on 0-rivi, joten jollain b:llä

saadaan 0:n kohdalle ei-nolla ja siten ristiriita. (Otetaan vaikka sellainen bmato, jossa viimeinen alkio on 1 ja muunnetaan se käänteisillä rivioparaatioilla.))

No, tämähän on aivan yleinen ominaisuus n-ulotteisille avaruuksille. Jos siinä on n vektoria, jotka ovat joko LRT tai virittävät, niin kyseessä on kanta.

>    v:=<1,2,3>;

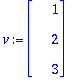
v := Vector(%id = 138616996)

>    c:=LinearSolve(A,v);

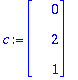
c := Vector(%id = 138617076)

>    c[1]*v1+c[2]*v2+c[3]*v3;

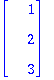
Vector(%id = 138617116)

Oikein meni!

5.

>    A:=<<4,-1,0,-1,0,0>|<-1,4,-1,0,-1,0>|<0,-1,4,0,0,-1>|<-1,0,0,4,-1,0>|<0,-1,0,-1,4,-1>|<0,0,-1,0,-1,4>>;
b:=<30,20,60,30,20,60>;

A := Matrix(%id = 138020272)

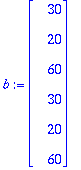
b := Vector(%id = 134675072)

Tästä on hyvä jatkaa LV:lla.
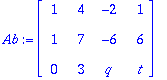
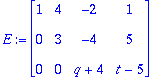
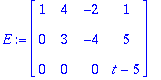
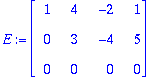
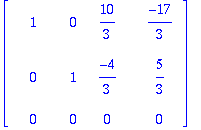