Normaalimoodit yleisesti
| > | u:=(n,x,t)->cos(c*n*Pi*t/L)*sin(n*Pi*x/L); |
![]()
| > | L:=2: c:=3: |
| > | plot3d(u(1,x,t),x=0..L,t=0..5,axes=boxed): |
| > | kuvax:=(n,t)->plot(u(n,x,t),x=0..L): |
| > | kuvax(1,0); |
| > | h:=0.05: N:=30: |
| > | display(seq(kuvax(1,t),t=[seq(j*h,j=0..N)]),insequence=true): |
| > | plot3d(u(3,x,t),x=0..L,t=0..5,axes=boxed,grid=[20,70]): |
| > | h:=0.05: N:=30: |
| > | display(seq(kuvax(3,t),t=[seq(j*h,j=0..N)]),insequence=true); |
| > | display(seq(kuvax(5,t),t=[seq(j*h,j=0..N)]),insequence=false); |
| > |
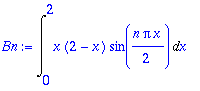
![[Maple Plot]](images/harj12lv8.gif)
![[Maple Plot]](images/harj12lv10.gif)
![[Maple Plot]](images/harj12lv11.gif)