Harj11AV
ti 24.11.02
Alustukset, muista editoida kaikki read-lauseet oman polkumäärityksesi mukaan.
Huomaa, että
read
-lauseita esiintyy jokaisen
restartin
jälkeen.
Warning, the name changecoords has been redefined
| > |
#read("/p/edu/mat-1.414/maple/v302.mpl"):
|
| > |
#read("c:\\usr\\heikki\\s02\\v302.mpl"):
|
| > |
read("/home/apiola/opetus/peruskurssi/v2-3/maple/v302.mpl"):
|
| > |
plots[setoptions](axes=boxed):
|
Fourier-kertoimet
Otetaan "pedagogisista syistä" ensin
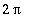 -jaksoinen ja sitten yleinen.
-jaksoinen ja sitten yleinen.
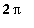 -jaksoinen funktio f
-jaksoinen funktio f
| > |
a0:=(1/(2*Pi))*Int(f(x),x=-Pi..Pi);
|
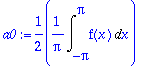
| > |
an:=(1/Pi)*Int(f(x)*cos(n*x),x=-Pi..Pi);
|
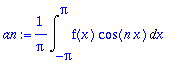
| > |
bn:=(1/Pi)*Int(f(x)*sin(n*x),x=-Pi..Pi);
|
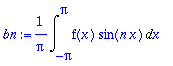
| > |
sarja:='a0'+Sum('an'*cos(n*x)+'bn'*sin(n*x),n=1..infinity);
|
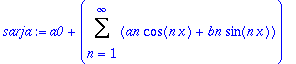
| > |
osasumma:=(x,N)->a0+add(an*cos(n*x)+bn*sin(n*x),n=1..N):
|
1.
| > |
f:=x->piecewise(-Pi < x and x < 0, 0,0 < x and x < Pi/2, 1,Pi/2 < x and x < Pi,0);
|
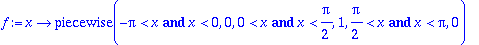
![[Maple Plot]](images/harj11av8.gif)
![[Maple Plot]](images/harj11av9.gif)
Lasketaanpa Fourier-kertoimet:
| > |
a0:=(1/(2*Pi))*Int(f(x),x=-Pi..Pi);
|
![a0 := 1/2*1/Pi*Int(PIECEWISE([0, -Pi-x < 0 and x < 0],[1, -x < 0 and x-1/2*Pi < 0],[0, -x+1/2*Pi < 0 and x-Pi < 0]),x = -Pi .. Pi)](images/harj11av10.gif)
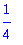
Käsin laskisimme näin:
| > |
a0:=1/(2*Pi)*int(1,x=0..Pi/2);
|
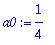
![a[n]](images/harj11av13.gif) : Annetaan ensin Maplen laskea automaattisesti:
: Annetaan ensin Maplen laskea automaattisesti:
| > |
an:=(1/Pi)*Int(f(x)*cos(n*x),x=-Pi..Pi);
|
![an := 1/Pi*Int(PIECEWISE([0, -Pi-x < 0 and x < 0],[1, -x < 0 and x-1/2*Pi < 0],[0, -x+1/2*Pi < 0 and x-Pi < 0])*cos(n*x),x = -Pi .. Pi)](images/harj11av14.gif)
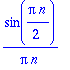
Käsin laskien:
| > |
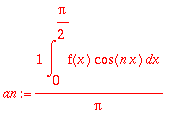
|
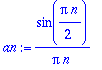
Nähtiin samalla, että Maplen int hallitsee piecewise-määritellyn funktion. (Tällaiset seikat on hyvä aina varmistaa, kannattaa muistaa, että
symbolilaskentaohjelman tekeminen on erittäin vaativa homma, ja ohjelman tekijätkin ovat inhimilliyydestään johtuen erehtyväisiä.)
| > |
bn:=(1/Pi)*Int(f(x)*sin(n*x),x=-Pi..Pi);
|
![bn := 1/Pi*Int(PIECEWISE([0, -Pi-x < 0 and x < 0],[1, -x < 0 and x-1/2*Pi < 0],[0, -x+1/2*Pi < 0 and x-Pi < 0])*sin(n*x),x = -Pi .. Pi)](images/harj11av18.gif)
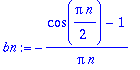
Käsin:
| > |
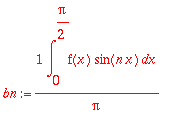
|
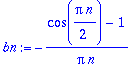
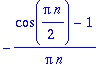
| > |
seq(an,n=1..10);
seq(bn,n=1..10);
|
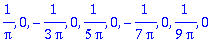
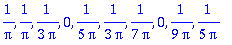
| > |
sarja:='a0'+Sum('an'*cos(n*x)+'bn'*sin(n*x),n=1..infinity);
|
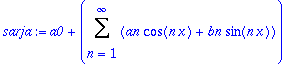
| > |
osasumma:=(x,N)->a0+add(an*cos(n*x)+bn*sin(n*x),n=1..N):
|
| > |
plot([f(x),osasumma(x,5)],x=-Pi..Pi);
|
![[Maple Plot]](images/harj11av26.gif)
| > |
plot([f(x),seq(osasumma(x,N),N=1..20)],x=-Pi..Pi);
|
![[Maple Plot]](images/harj11av27.gif)
| > |
plot([Jf(x),seq(osasumma(x,N),N=21..40)],x=-2*Pi..2*Pi);
|
![[Maple Plot]](images/harj11av28.gif)
| > |
plot([f(x),osasumma(x,50)],x=-Pi..Pi,color=[gray,blue],numpoints=150);
|
![[Maple Plot]](images/harj11av29.gif)
Suppenemislauseen ehdot: paloittain jatkuvuus ja vp. ja op. derivoituvuus ovat voimassa. Niinpä sarja suppenee kohti funktion arvoa kaikkialla
muualla paitsi pisteissä
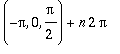 . Näissä se suppenee kohti arvoa
. Näissä se suppenee kohti arvoa
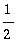 .
.
2.
(a)
Seuraa suoraan integraalin lineaarisuudesta.
| > |
kanttisarja:=(4/Pi)*Sum(sin(2*k-1)*x/(2*k-1),k=1..infinity);
|
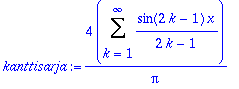
Olkoon
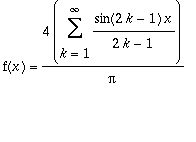 .
.
Suoritetaan ensin muuttujan skaalaus uudelle jaksovälille [-1,1]. Olkoon
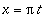 . Merk
. Merk
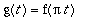 .
.
g(t) =
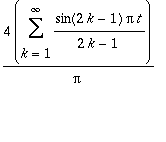
u(t) saadaan g(t):stä lisäämällä 1 ja jakamalla 2:lla:
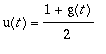 .
.
| > |
usarja:=(1+(4/Pi)*Sum(sin((2*k-1)*Pi*t)/(2*k-1),k=1..infinity))/2;
|
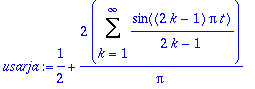
| > |
osasumma:=(t,N)->(1+(4/Pi)*add(sin((2*k-1)*Pi*t)/(2*k-1),k=1..N))/2;
|
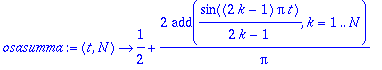
| > |
plot(osasumma(t,10),t=-2..2,numpoints=100);
|
![[Maple Plot]](images/harj11av40.gif)
Hyvältä näyttää!
3.
Warning, the name changecoords has been redefined
a)
Summa
:
Olk.
![f[1]](images/harj11av41.gif) ja
ja
![f[2]](images/harj11av42.gif) parillisia. Olkoon
parillisia. Olkoon
![f = f[1]+f[2]](images/harj11av43.gif) .
.
+f[2](-x)](images/harj11av44.gif) =
=
+f[2](x)](images/harj11av45.gif) =
f(x)
, koska kerran
=
f(x)
, koska kerran
![f[1]](images/harj11av46.gif) ja
ja
![f[2]](images/harj11av47.gif) parillisia.
parillisia.
Olk.
![f[1]](images/harj11av48.gif) ja
ja
![f[2]](images/harj11av49.gif) parittomia. Olkoon
parittomia. Olkoon
![f = f[1]+f[2]](images/harj11av50.gif) .
.
+f[2](-x)](images/harj11av51.gif) =
=
-f[2](x)](images/harj11av52.gif) =
=
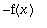 , koska kerran
, koska kerran
![f[1]](images/harj11av54.gif) ja
ja
![f[2]](images/harj11av55.gif) parittomia.
parittomia.
Tulot:
Olkoon
![f[1]](images/harj11av56.gif) pariton ja
pariton ja
![f[2]](images/harj11av57.gif) parillinen. Olkoon
parillinen. Olkoon
![f = f[1]*f[2]](images/harj11av58.gif) .
.
*f[2](-x)](images/harj11av59.gif) =
=
*f[2](x)](images/harj11av60.gif) =
=
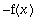 .
.
Siis parittoman ja parillisen tulo on pariton.
Muut aivan vastaavasti: pariton x pariton = parillinen, parillinen x parillinen = parillinen.
b)
Olkoon f annettu realifunktio.
| > |
fplus:=x->f(x)+f(-x); fmiinus:=x->f(x)-f(-x);
|
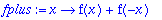
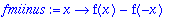
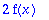
| > |
fe:=fplus/2; fo:=fmiinus/2;
|
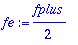
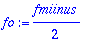
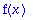
| > |
fe(-x)=fe(x); # Niin on.
|
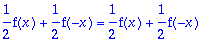
| > |
fo(-x)=-fo(x); # ja näin on.
|
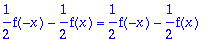
Niinpä f voidaan esittää muodossa
+f[o](x)](images/harj11av70.gif) ,
,
missä
 = (f(x)+f(-x))/2](images/harj11av71.gif) ja
ja
 = (f(x)-f(-x))/2](images/harj11av72.gif) .
.
![f[e]](images/harj11av73.gif) :tä on luonnollista nimittää f:n parilliseksi osaksi ja
:tä on luonnollista nimittää f:n parilliseksi osaksi ja
![f[o]](images/harj11av74.gif) :ta parittomaksi osaksi.
:ta parittomaksi osaksi.
Huom!
Nämä ovat eri asioita kuin parillinen ja pariton laajennus, vaikka käytämme samoja merkintöjä. Fourier-sarjojen teoriassa
l
a
ajennukset
ovat tärkeämmässä osassa
.
c)
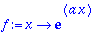
| > |
fe:=(f(x)+f(-x))/2; convert(fe,trig);
|
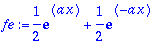
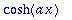
| > |
fo:=(f(x)-f(-x))/2; convert(fo,trig);
|
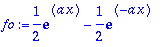
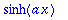
Siis
hyperbolinen cos
on
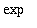 -funktion
parillinen osa
ja
hyperbolinen sin
on
pariton osa
.
-funktion
parillinen osa
ja
hyperbolinen sin
on
pariton osa
.
4.
Funktio f : [0,L] --> R voidaan laajentaa parilliseksi määrittelemällä
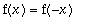 ja
ja
parittomaksi määrittelemällä
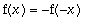 , kun x < 0 .
, kun x < 0 .
Esim:
| > |
Oef:=piecewise(x<0,-f(-x),x>0,f(x)); # Odd extension (of) f
|
![Oef := PIECEWISE([-exp(-x), x < 0],[exp(x), 0 < x])](images/harj11av83.gif)
| > |
Eef:=piecewise(x<0,f(-x),x>0,f(x)); # Even extension (of) f
|
![Eef := PIECEWISE([exp(-x), x < 0],[exp(x), 0 < x])](images/harj11av84.gif)
![[Maple Plot]](images/harj11av85.gif)
![[Maple Plot]](images/harj11av86.gif)
Asiaan:
-
Jos f on pariton, niin
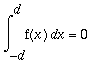 ,
,
-
Jos f on parillinen, niin
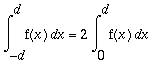 .
.
Havainnollisesti, pinta-aloja ajattelemalla asia on aivan selvä, voidaan perustella täsmällisesti vaikka Riemannin summilla,
tai sitten muuttujan vaihdolla integraaleissa (uusi muuttuja -x).
a) Jos f : [0,L] --> R jatketaan parilliseksi, on kyseessä parillisen jatkon
![f[e]](images/harj11av89.gif) sarja, jolloin
sarja, jolloin
![b[n]](images/harj11av90.gif) -kertoimet ovat nollia, koska
-kertoimet ovat nollia, koska
![b[n] := 1/L*Int(f[e](x)*sin(n*x),x = -L .. L)](images/harj11av91.gif) ;
;
ja integroitavana on siis (parillinen
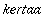 pariton), joten tulos = 0.
pariton), joten tulos = 0.
Tällöin
![a[0] = 1/2/L*Int(f[e](x),x = -L .. L)](images/harj11av93.gif) =
=
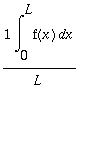 .
.
Vastaava kaava pätee muillekin
![a[n]](images/harj11av95.gif) - kertoimille, koska
- kertoimille, koska
![f[e]*cos](images/harj11av96.gif) on
parillinen
funktio.
on
parillinen
funktio.
Siis:
![a[n] = 1/L*Int(f[e](x)*cos(n*Pi*x/L),x = -L .. L)](images/harj11av97.gif) =
=
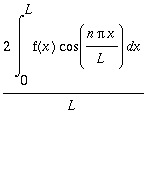
b) Jos f : [0,L] --> R jatketaan parittomaksi, on kyseessä parittoman jatkon
![f[o]](images/harj11av99.gif) sarja, jolloin
sarja, jolloin
![a[n]](images/harj11av100.gif) -kertoimet ovat nollia, koska
-kertoimet ovat nollia, koska
![a[n] := 1/L*Int(f[o](x)*cos(n*Pi*x/L),x = -L .. L)](images/harj11av101.gif) ;
;
ja
integroitavana
on siis (pariton
 parillinen), eli
pariton funktio
, joten tulos = 0.
parillinen), eli
pariton funktio
, joten tulos = 0.
Tällöin:
![b[n] := 1/L*Int(f[o](x)*sin(n*Pi*x/L),x = -L .. L)](images/harj11av103.gif) =
=
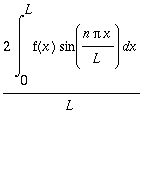
Nämä kaavat pätevät pätevät tietysti aina, kun kyseessä on välillä [-L,L] määritelty (a) parillinen tai (b) pariton
funktio, jolloin niiden käyttö säästää hieman laskuvaivaa.
Parillisen/parittoman jatkamisen tilanteessa kaavoilla on suurempi merkitys sikäli, että niiden avulla saadaan
yksinkertaiset laskukaavat alkuperäisen, välillä [0,L] määritellyn funktion f avulla lausuttuna.
5.
Warning, the name changecoords has been redefined
| > |
#read("/p/edu/mat-1.414/maple/v302.mpl"):
|
| > |
#read("c:\\usr\\heikki\\s02\\v302.mpl"):
|
| > |
read("/home/apiola/opetus/peruskurssi/v2-3/maple/v302.mpl"):
|
| > |
plots[setoptions](axes=boxed):
|
Tiedostossa v302.mpl on määritelty pariton ja parillinen jatkamisoperaattori. Kun halutaan määritellä funktio
(operaattori), joka palauttaa funktion, niin käytetään unapply-tapaa.
Matemaattisesti looginen olisi myös tapa:
| > |
ptonj:=f->(x->piecewise(0 < x,f(x),x < 0,-f(-x)));
|

Ahaa, Maple 8:ssa tämä toimii, vanhemmissa varmaan ei.
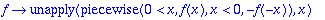
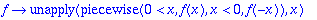
| > |
fe:=parillinenjatko(f);fo:=paritonjatko(f);
|


| > |
plot([fo,fe+0.1],-4..4,title="Funktion f(x)=x parill. ja pariton jatko"); # Piirretään fe+0.1, jotta erottuvat.
|
![[Maple Plot]](images/harj11av110.gif)


| > |
plot(Jfe,-8..8); plot(Jfo,-8..8);
|
![[Maple Plot]](images/harj11av113.gif)
![[Maple Plot]](images/harj11av114.gif)
Parillinen laajennus:
| > |
a0:=(1/L)*Int(f(x),x=0..L);a0:=value(a0);
|
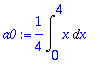
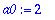
| > |
an:=(2/L)*Int(f(x)*cos(n*Pi*x/L),x=0..L);an:=value(an);
|
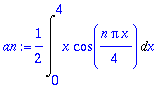
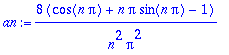
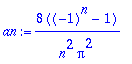
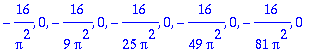
| > |
seq(-16/Pi^2/(2*k-1)^2,k=1..5);
|
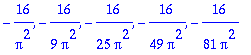
| > |
ak:=-16/Pi^2/(2*k-1)^2;
|
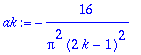
| > |
sarja:=a0+Sum(ak*cos((2*k-1)*Pi*x/L),k=1..infinity);
|
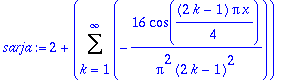
| > |
osasumma:=unapply(a0+sum(ak*cos((2*k-1)*Pi*x/L),k=1..K),x,K);
|
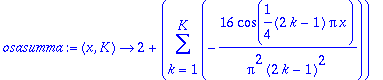
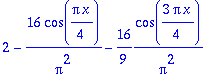
| > |
plot([Jfe(x),seq(osasumma(x,j),j=1..7)],x=-8..8);
|
![[Maple Plot]](images/harj11av126.gif)
Pariton laajennus:
| > |
bn:=(2/L)*Int(f(x)*sin(n*Pi*x/L),x=0..L);bn:=value(bn);
|
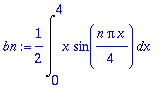
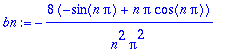
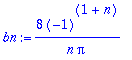
| > |
sarja:=Sum(bn*sin(n*Pi*x/L),n=1..infinity);
|
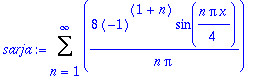
| > |
osasumma:=unapply(sum(bn*sin(n*Pi*x/L),n=1..N),x,N);
|
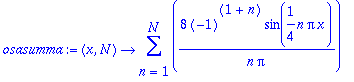
| > |
plot([Jfo(x),osasumma(x,5)],x=-8..8);
|
![[Maple Plot]](images/harj11av132.gif)
| > |
plot([Jfo(x),osasumma(x,10)],x=-4..4);
|
![[Maple Plot]](images/harj11av133.gif)
Tässä nyt on mukana jo LV-tehtävääkin, tarkistuksen vuoksi.
Suppenemislauseen soveltaminen on hyvin mekaanista.
Parillinen laajennus
on kaikkialla jatkuva, suppenemiskäytös on hämmästyttävän hyvä.
Lauseen mukaan suppenee kaikkialla kohti f:n arvoa.
Pariton laajennus on epäjatkuva päätepisteissä 4 + k*8, (k=+-1,+-2,...). Kuva vahvistaa lauseen väitteen, mikä näkyy suoraan
sarjasta sijoittamalla x=k*4.
6.
Tässä olis ollut hyvä antaa sarjan muoto, jota haetaan, tosin KRE-kirja pitäisi olla useimmilla, sieltähän löytyy.
Warning, the name changecoords has been redefined
| > |
sarja:=Sum(c[n]*exp(i*n*x),n=-infinity..infinity);
|
![sarja := Sum(c[n]*exp(i*n*x),n = -infinity .. infinity)](images/harj11av134.gif)
Kun puhutaan systeemin
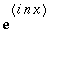 ortogonaalisuudesta, on luonnollista laskea :
ortogonaalisuudesta, on luonnollista laskea :
| > |
Int(exp(I*n*x)*exp(-I*k*x),x=-Pi..Pi);
|
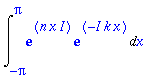
Sillä sisätulo kompleksikertoimisessa avaruudessa vaatii jälkimmäisen argumentin konjugoinnin. Tämä ei sinänsä
ole tehtävän kannalta välttämätön tieto, koska käydään joka tapauksessa läpi kaikki kokonaisindeksit.
| > |
int(exp(I*n*x)*exp(-I*k*x),x);
|
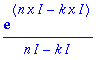
Tämä lasku on voimassa, jos
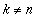 , jolloin sijoitus
, jolloin sijoitus
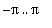 antaa 0 (
antaa 0 (
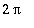 -jaksoinen funktio).
-jaksoinen funktio).
Jos k=n, saadaan
| > |
exp(I*n*x)*exp(-I*n*x)=1;
|
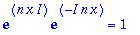
joten
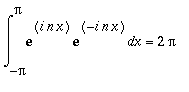 .
.
Jos siis f:llä on sarjaesitys:
| > |
f(x) = Sum(c[n]*exp(i*n*x),n = -infinity .. infinity);
|
![f(x) = Sum(c[n]*exp(i*n*x),n = -infinity .. infinity)](images/harj11av143.gif)
niin kertomalla exp(-i*k*x):llä ja integroimalla saadaan:
![Int(f(x)*exp(-i*k*x),x = -Pi .. Pi) = Sum(c[n]*Int(exp(-i*k*x)*exp(i*n*x),x = -Pi .. Pi),n = -infinity .. infinity)](images/harj11av144.gif)
Nollasta poikkeavaa tulee vain, kun n=k, jolloin integraali = 2*Pi .
Niinpä saadaan:
![c[k] = Int(f(x)*exp(i*k*x),x = -Pi .. Pi)/2/Pi](images/harj11av145.gif) .
.
Huom!: On makuasia, kummassa on miinusmerkki, sarjassa vai kertoimessa.
Todella kaunis ja symmetrinen muoto, ja vähällä vaivalla! Tämä on myös oikea muoto lähestyttäessä Fourier-muunnosta.
![]() -jaksoinen ja sitten yleinen.
-jaksoinen ja sitten yleinen.
![]() -jaksoinen funktio f
-jaksoinen funktio f
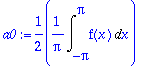
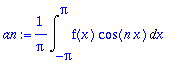
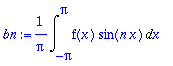
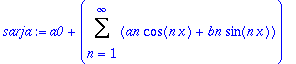
![[Maple Plot]](images/harj11av8.gif)
![[Maple Plot]](images/harj11av9.gif)
![a0 := 1/2*1/Pi*Int(PIECEWISE([0, -Pi-x < 0 and x < 0],[1, -x < 0 and x-1/2*Pi < 0],[0, -x+1/2*Pi < 0 and x-Pi < 0]),x = -Pi .. Pi)](images/harj11av10.gif)
![an := 1/Pi*Int(PIECEWISE([0, -Pi-x < 0 and x < 0],[1, -x < 0 and x-1/2*Pi < 0],[0, -x+1/2*Pi < 0 and x-Pi < 0])*cos(n*x),x = -Pi .. Pi)](images/harj11av14.gif)

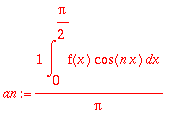
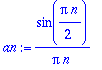
![bn := 1/Pi*Int(PIECEWISE([0, -Pi-x < 0 and x < 0],[1, -x < 0 and x-1/2*Pi < 0],[0, -x+1/2*Pi < 0 and x-Pi < 0])*sin(n*x),x = -Pi .. Pi)](images/harj11av18.gif)

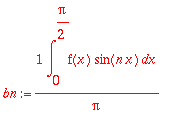

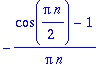
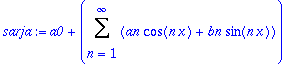
![[Maple Plot]](images/harj11av26.gif)
![[Maple Plot]](images/harj11av27.gif)
![[Maple Plot]](images/harj11av28.gif)
![[Maple Plot]](images/harj11av29.gif)
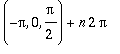 . Näissä se suppenee kohti arvoa
. Näissä se suppenee kohti arvoa
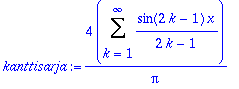
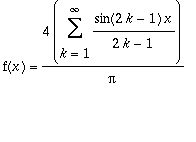 .
.
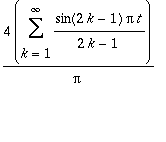
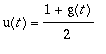 .
.
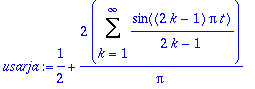
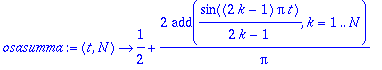
![[Maple Plot]](images/harj11av40.gif)
 = (f(x)+f(-x))/2](images/harj11av71.gif) ja
ja
 = (f(x)-f(-x))/2](images/harj11av72.gif) .
.
![Oef := PIECEWISE([-exp(-x), x < 0],[exp(x), 0 < x])](images/harj11av83.gif)
![Eef := PIECEWISE([exp(-x), x < 0],[exp(x), 0 < x])](images/harj11av84.gif)
![[Maple Plot]](images/harj11av85.gif)
![[Maple Plot]](images/harj11av86.gif)
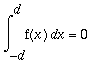 ,
,
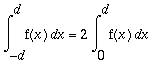 .
.
![b[n] := 1/L*Int(f[e](x)*sin(n*x),x = -L .. L)](images/harj11av91.gif) ;
;
![a[0] = 1/2/L*Int(f[e](x),x = -L .. L)](images/harj11av93.gif) =
=
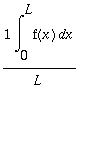 .
.
![a[n] = 1/L*Int(f[e](x)*cos(n*Pi*x/L),x = -L .. L)](images/harj11av97.gif) =
=
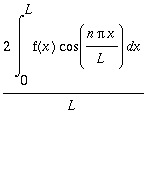
![a[n] := 1/L*Int(f[o](x)*cos(n*Pi*x/L),x = -L .. L)](images/harj11av101.gif) ;
;
![b[n] := 1/L*Int(f[o](x)*sin(n*Pi*x/L),x = -L .. L)](images/harj11av103.gif) =
=
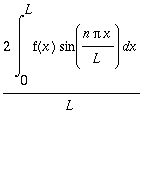
![[Maple Plot]](images/harj11av110.gif)
![[Maple Plot]](images/harj11av113.gif)
![[Maple Plot]](images/harj11av114.gif)
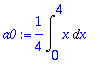
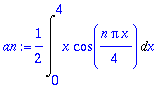
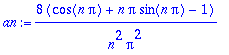
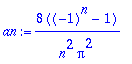
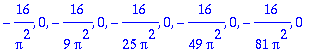
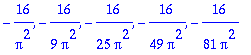
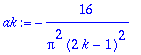
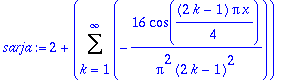
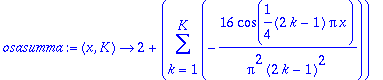
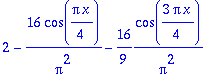
![[Maple Plot]](images/harj11av126.gif)
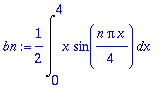
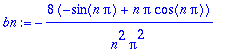
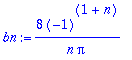
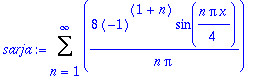
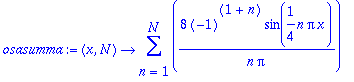
![[Maple Plot]](images/harj11av132.gif)
![[Maple Plot]](images/harj11av133.gif)
![sarja := Sum(c[n]*exp(i*n*x),n = -infinity .. infinity)](images/harj11av134.gif)
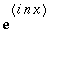 ortogonaalisuudesta, on luonnollista laskea :
ortogonaalisuudesta, on luonnollista laskea :
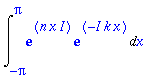
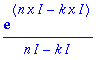
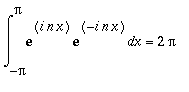 .
.
![f(x) = Sum(c[n]*exp(i*n*x),n = -infinity .. infinity)](images/harj11av143.gif)
![Int(f(x)*exp(-i*k*x),x = -Pi .. Pi) = Sum(c[n]*Int(exp(-i*k*x)*exp(i*n*x),x = -Pi .. Pi),n = -infinity .. infinity)](images/harj11av144.gif)
![c[k] = Int(f(x)*exp(i*k*x),x = -Pi .. Pi)/2/Pi](images/harj11av145.gif) .
.