1.
| > | restart: with(inttrans): alias(LL=laplace,IL=invlaplace,u=Heaviside): # Joudumme käyttämään LL-nimea, koska L on tässä tehtävässä varattu kelan induktanssille. |
| > | RC:=int(i1(tau),tau=0..t)/C+R*i2(t)=e(t); |
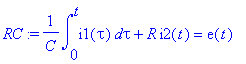
| > | RL:=L*diff(i1(t),t)-L*diff(i2(t),t)=R*i2(t); |
![]()
| > | L:=2;C:=50*10^(-6);R:=100;e:=t->50*sin(100*t); |
![]()
![]()
![]()
![]()
| > | LRC:=LL(RC,t,s); |
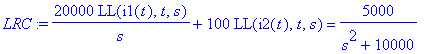
| > | LRL:=LL(RL,t,s); |
![]()
| > | AE:=i1(0)=0,i2(0)=0; |
![]()
| > | LRC:=subs(AE,LRC);LRL:=subs(AE,LRL); |
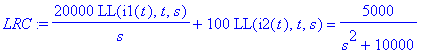
![]()
| > | solve({LRC,LRL},{LL(i1(t),t,s),LL(i2(t),t,s)}); |
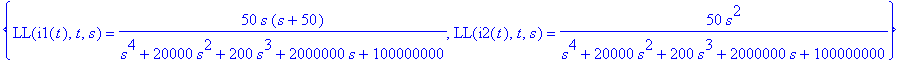
| > | I12:=subs(%,[LL(i1(t),t,s),LL(i2(t),t,s)]); |
![I12 := [50*s*(s+50)/(s^4+20000*s^2+200*s^3+2000000*s+100000000), 50/(s^4+20000*s^2+200*s^3+2000000*s+100000000)*s^2]](images/harj10lv13.gif)
| > | I1:=I12[1]: I2:=I12[2]: |
| > | I1:=convert(I1,parfrac,s);I2:=convert(I2,parfrac,s); |
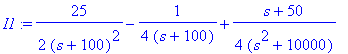
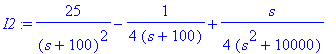
| > | i1:=IL(I1,s,t); |
![]()
| > | i2:=IL(I2,s,t); |
![]()
| > | plot([e(t)/R,i1,i2],t=0..3/10,color=[gray,red,blue],legend=["Syöttöjännite normeerattuna R:llä","Virta i1","Virta i2"]); |
![[Maple Plot]](images/harj10lv18.gif)
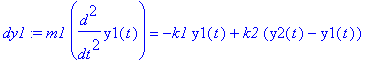
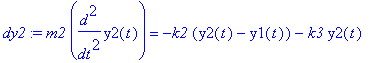
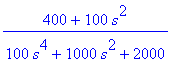
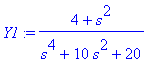
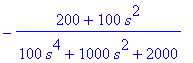
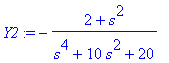
![[Maple Plot]](images/harj10lv46.gif)
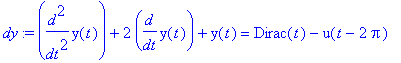
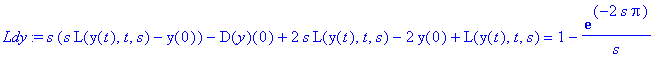
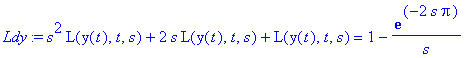
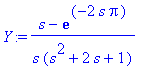
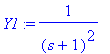
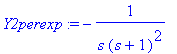
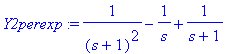
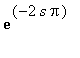 aiheuttaa t-siirron
aiheuttaa t-siirron
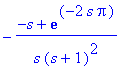
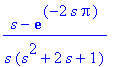
![[Maple Plot]](images/harj10lv63.gif)
![[Maple Plot]](images/harj10lv64.gif)
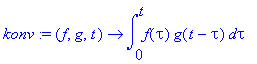
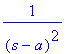
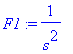
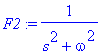
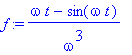
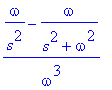
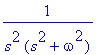
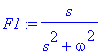
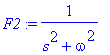
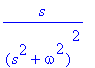
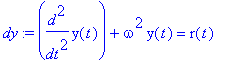
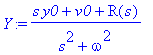
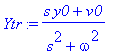
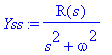
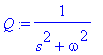
![[Maple Plot]](images/harj10lv98.gif)
![[Maple Plot]](images/harj10lv107.gif)
 .
.
![[Maple Plot]](images/harj10lv115.gif)
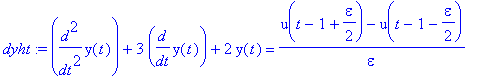
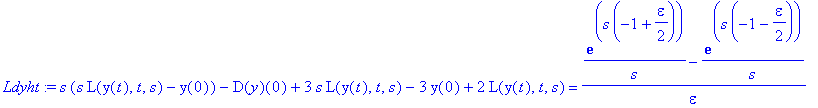
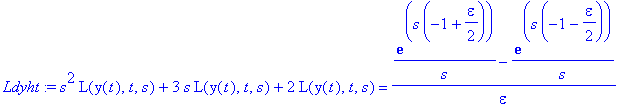
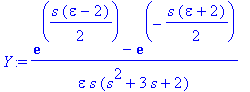
![[Maple Plot]](images/harj10lv129.gif)
![[Maple Plot]](images/harj10lv141.gif)
![[Maple Plot]](images/harj10lv142.gif)
![[Maple Plot]](images/harj10lv143.gif)
![[Maple Plot]](images/harj10lv144.gif)