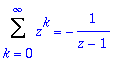
Sarjat, osa 2 funktiosarjat

V2/2002 tammi-helmikuu HA L/sarjat2.mws

Osassa 1 käsittelemme vakiotermisiä sarjoja, nyt on funktiosarjojen vuoro.

Sarjakehitelmien johtamista algebrallisten ja der/int-lauseiden avulla

> Sum(z^k,k=0..infinity): %=value(%); # Maple osaa geometrisen sarjan etu- ja takaperin.

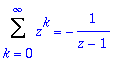
> series(1/(1-z),z=0,10);

> poly9:=convert(%,polynom);

Kerrotaan ja derivoidaan sarjoja

> f:=1/(1-z); sarja:=series(f,z=0,7); poly7:=convert(sarja,polynom);

> f^2=expand(poly7^2)+R; #Maple ei tee sievennyksiä sarjamuodossa, siksi joudumme operoimaan polynomilla ja lisäämään omin päin virhetermin R.

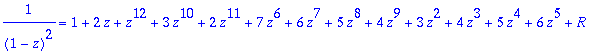
> f^3=expand(poly7^3)+R;

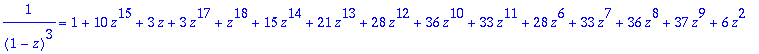
Maple järjestää miten sattuu. Polynomin järjestäminen kasvavien potenssien mukaan käy hyvin kehittämällä se Taylorin polynomiksi, jonka asteluku on vähintään polynomin oma asteluku. (Polynomifunktio säilyy tässä operaatiossa identtisenä.)

> taylor(poly7^3,z=0,22); # expand ei ole tässä tarpeen.

Maple tekee "likaisen työn" käden käänteessä, meidän tulee tietää rajat, joissa tulokset ovat voimassa.

Katsotaan, mitä saadaan derivoimalla 4 kertaa:

> d4f:=diff(f,z$4);

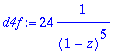
> sarja:=series(f,z=0,15);

> d4f=diff(sarja,z$4); # Maple suostuu derivoimaan sarjaa, ei siis tarvitse katkaista, kuten edellä.

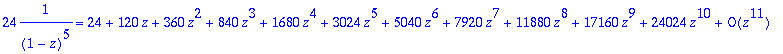
Maple tekee, mitä käsketään. Me tiedämme [PSD]-lauseen nojalla, että operaation on voimassa suppenemiskiekossa | z | < 1 .

> map(lauseke->lauseke/24,%); # Elegantti tapa jakaa puolittain 24:llä.

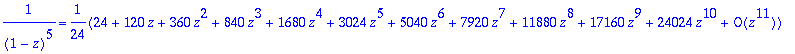
Näin saatiin sarjakehitelmän alku.

Ryhdytään piirtelemään.

> with(plots):

> eps:=0.1: plot(f,z=-1..1-eps);

> sarjakuva3:=plot(convert(series(f,z=0,3),polynom),z=-1..1-eps,color=blue):
sarjakuva5:=plot(convert(series(f,z=0,5),polynom),z=-1..1-eps,color=green):
sarjakuva10:=plot(convert(series(f,z=0,10),polynom),z=-1..1-eps,color=black):

> display(plot(f,z=-1..1-eps),sarjakuva3,sarjakuva5,sarjakuva10);

> display(plot(f,z=-1..1-eps),display(sarjakuva3,sarjakuva5,sarjakuva10,insequence=true));

Taylorin sarjat

Aloitetaan exp-funktiosta. Maple on erinomainen derivointi- ja sievennysapulainen. Voimme tehdä omin käsin Taylorin polynomia niin pitkälle kuin haluamme.

> restart:

Warning, the name changecoords has been redefined

> f:=exp(x); n:=10:

> derivaatat:=[seq(diff(f,x$k),k=1..n)];

> kertoimet:=eval(subs(x=0,derivaatat));

> kertoimet:=eval(subs(x=0,f)),op(kertoimet); # Maple ei tunne 0:tta derivaattaa, siksi liitettiin 1 eteen.

> kertoimet:=seq(kertoimet[k]/(k-1)!,k=1..n+1);

> Pn:=sum(kertoimet[k]*x^(k-1),k=1..n+1);

Vaihtoehtoisesti for-lauseella

> restart:f:=exp(x); n:=10:

Warning, the name changecoords has been redefined

> d[0]:=f: a[0]:=subs(x=0,f): for k from 1 to n do d[k]:=simplify(diff(d[k-1],x));a[k]:=eval(subs(x=0,d[k]))/k!; od: k:='k':

> Pn:=sum(a[k]*x^k,k=0..n);

Tämä on laskennallisesti sikäli järkevämpi, että derivaatat lasketaan peräjälkeen, eikä edellisellä tuhlailevalla tavalla. Toinen etu on, että nyt voidaan indekskointi aloittaa myös 0:sta.

(Maplen taulukko ja lista hoidetaan hakasulkuindeksoinnilla. Taulukon indeksointi on aivan vapaa, voidaan käyttää vaikka symbolisia indeksejä (kuten plots[display] ).

Verrataan valmiiseen Tayloriin:

> taylor(f,x=0,11);

> series(f,x=0,11);

Voimme nyt kehittää periaatteessa minkä vain funktion. Mukavammalta tuntuu ensin tehdä omin avuin:

> restart:f:=sin(x); n:=15:
derivaatat:=[seq(diff(f,x$k),k=1..n)];
kertoimet:=eval(subs(x=0,derivaatat));
kertoimet:=eval(subs(x=0,f)),op(kertoimet); # Maple ei tunne 0:tta derivaattaa, siksi liitettiin 1 eteen.
kertoimet:=seq(kertoimet[k]/(k-1)!,k=1..n+1);
Pn:=sum(kertoimet[k]*x^(k-1),k=1..n+1);

Warning, the name changecoords has been redefined

> plot([f,Pn],x=-2.5*Pi..2.5*Pi,color=[red,blue]);

>

>

> taysinkuva:=n->plot(convert(taylor(sin(x),x=0,n+1),polynom),x=-Pi..Pi):

> display(plot(sin(x),x=-Pi..Pi,color=blue),seq(taysinkuva(n),n=1..11));

> display(plot(sin(x),x=-Pi..Pi,y=-1..1,color=blue),display(seq(taysinkuva(n),n=1..11),insequence=true));

Funktio/operaattorityyli

Kätevämmin saadaan tuo omaperäinen ratkaisutapa aikaan määrittelemällä f funktioksi ja käyttämällä derivaatta-operaattoria D.

> restart:

Warning, the name changecoords has been redefined

> f:=cos:

> seq((D@@k)(f)(0),k=0..10);

> n:=4: sum(((D@@k)(f)(z0)/k!)*(z-z0)^k,k=0..n);

Rakennetaan tämä taypol -funktioksi, joka on aivan yhtä helppokäyttöinen kuin valmis

taylor (taylorissa on "sarja-tietorakenne", me tyydymme polynomiin, sitä useimmin tarvitsemme).

> taypol:=(f,z0,n)->sum(((D@@k)(f)(z0)/k!)*(z-z0)^k,k=0..n);

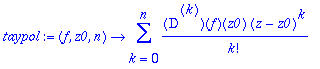
> taypol(sin,0,10);

> taypol(x->sin(x)*exp(-x),0,4);

> taylor(sin(x)*exp(-x),x=0,5);

>

>