Sarjat HA
L to 24.1.02
p-harmoniset sarjat
> seq(sum(1./n,n=1..m),m=1..100);
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
> log(100.);
![]()
> seq(evalf(log(m)),m=1..100);
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
> plot([seq([m,sum(1./n,n=1..m)],m=1..100)],style=point);
![[Maple Plot]](images/sarjat22.gif)
> sum(1./n,n=1..1000);
![]()
>
> ithprime(10);
![]()
> ?prime
> seq(sum(1./ithprime(k),k=1..N),N=[100,200,300]);
![]()
> seq(sum(1./ithprime(k),k=1..N),N=[100,500]);
![]()
>
> sum(1/n^2,n=1..infinity);
![]()
> sum(1/n^2,n=1..N);
![]()
> sum(1/n^3,n=1..N);
![]()
>
Vuorottelevat sarjat
> seq(Sum((-1)^(k-1)*1/k,k=1..n),n=1..10);
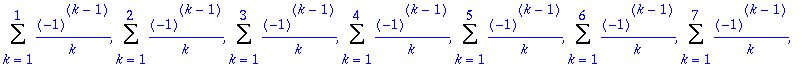
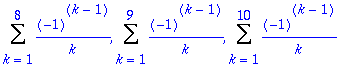
> map(value,[%]);
![]()
> evalf(%);
![]()
> evalf(seq(sum((-1)^(k-1)*1/k,k=1..n),n=1..30));
![]()
![]()
![]()
> evalf(seq(sum((-1)^(k-1)*1/k,k=1..n),n=[1,3,5,7,9]));
![]()
> evalf(seq(sum((-1)^(k-1)*1/k,k=1..n),n=[2,4,6,8,10]));
![]()
> evalf(sum((-1)^(k-1)*1/k,k=1..100));
![]()
> evalf(sum((-1)^(k-1)*1/k,k=1..101));
>
![]()
>
Havaitaan:
Parittomat osasummat muodostavat pienenevän jonon.
Parilliset muodostavat kasvavan jonon.
Jokainen pariton > mikä tahansa parillinen
Suurilla n:n arvoilla näyttävät lähestyvän toisiaan (joskin hitaasti).