Osittaisderivaattoja L/osder.mws
L ke-to 13-14.2.02 HA
Pystyleikkaustasoja
> restart:
Warning, the name changecoords has been redefined
> with(plots): setoptions3d(axes=BOXED):
> tasoleikkxz:=(f,y0,vali::range)->spacecurve([x,y0,f(x,y0)],x=vali):
> f:=(x,y)->x^2-y^2;
![]()
> tasoleikkxz(f,1,-2..2);
![[Maple Plot]](images/osder2.gif)
> tasoxz:=(y0,valix::range,valiz::range)->plot3d([x,y0,z],x=valix,z=valiz,grid=[5,5]):
> display(tasoleikkxz(f,1,-2..2),tasoxz(1,-2..2,-1..3),style=wireframe);
tangxz:=(f,x0,y0,xvali::range)->spacecurve([_x,y0,f(x0,y0)+D[1](f)(x0,y0)*(_x-x0)],_x=op(1,xvali)..op(2,xvali),color=red,thickness=2):
![[Maple Plot]](images/osder3.gif)
> plot3d(f(x,y),x=-2..2,y=0..2);
![[Maple Plot]](images/osder4.gif)
> display(tangxz(f,1,1,-1..3),tasoleikkxz(f,1,-3..3),tasoxz(1,-3..3,-4..7),style=wireframe,labels=[x,y,z]);
![[Maple Plot]](images/osder5.gif)
> display(tangxz(f,1,1,-1..3),tasoleikkxz(f,1,-3..3),tasoxz(1,-3..3,-4..7),plot3d(f(x,y),x=-2..3,y=-1..2),style=hidden,labels=[x,y,z]);
![[Maple Plot]](images/osder6.gif)
> display(%,style=patchcontour);
![[Maple Plot]](images/osder7.gif)
Osittaisderivaattojen laskeminen
Maple:ssa on kaksi derivointifunktiota: 1) diff ja 2) D .
Edellinen operoi lausekkeeseen ja palauttaa lausekkeen. Jälkimmäisen argumenttina on funktio ja se palauttaa
derivaatatfunktion. Edellinen sopii symbolisen lausekkeen käsittelyyn. Jälkimmäinen on kätevä, kun halutaan
laskea derivaatan arvoja annetuissa pisteissä.
Esim
Aluksi lauseketyyli.
> f:=sqrt(x+y^2); # Käsitellään lausekkeena.
![]()
> fx:=diff(f,x); fy:=diff(f,y);
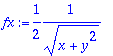
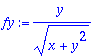
Lasketaan arvot pisteessä (0,2)
> simplify(subs(x=0,y=2,fx)); simplify(subs(x=0,y=2,fy));
![]()
![]()
Käsitellään nyt funktiotyylillä:
> f:=(x,y)->sqrt(x+y^2);
![]()
> f1:=D[1](f);f2:=D[2](f);
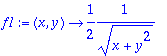
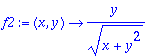
> f1(0,2);f2(0,2);
![]()
![]()
Esimerkiksi tangentin yhtälö on hyvin kätevää muodostaa funktiotyylillä, kts. tangxz .
Korkeammat derivaatat
> f:=x*exp(z)*arctan(y/x); # Käsitellään lausekkeena
![]()
> fx:=diff(f,x): fx:=map(simplify,%);
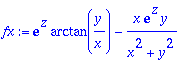
> fy:=simplify(diff(f,y));
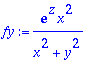
Voidaan jatkaa tästä derivointia. Maplen diff ottaa argumentikseen jonon derivoimismuuttujia. Siten voidaan suoraan laskea tähän tapaan:
> fxy:=simplify(diff(f,x,y));
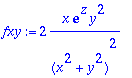
> fyx:=simplify(diff(f,y,x));
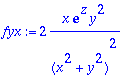
Samat näkyvä olevan!
Detivoidaan koko röykkiö (eräs 7. derivaatta)
> simplify(diff(f,x,z,x,y,z,y,x)); # 3 x:ää, 2 y:tä, 2 z:aa.
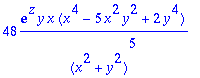
> simplify(diff(f,x,x,x,y,y,z,z));
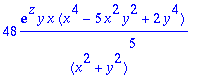
Sama tuli, kun järjestettin uudestaan.
Tehdään vielä operaattorityylillä:
> F:=(x,y,z)->x*exp(z)*arctan(y/x);
![]()
> D[1,1,1,2,2,3,3](F)(x,y,z): simplify(%);
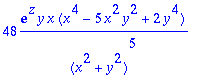
Ketjusääntö
> f:=sqrt(u(x,y)^2 + v(x,y)^2);
![]()
> diff(f,x);diff(f,y);
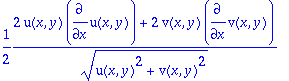
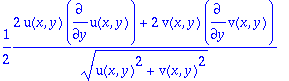
>
Maple osaa soveltaa ketjusääntöä ainakin yksinkertaisessa tapauksessa. Tietenkin se osaa soveltaa sitä yleisessäkin tapauksessa.
Lopetan nyt toistaiseksi tähän. Jos jatkoa seuraa, niin menköön työarkille osder2.mws. (13.2.02)