L/numint3.mws, esimerkkejä

V2 17.4.02 HA

Alustukset

> restart:

Warning, the name changecoords has been redefined

> #read("c:\\opetus\\maple\\v202.mpl"):

> #read("/p/edu/mat-1.414/maple/v202.mpl"):

> read("/home/apiola/opetus/peruskurssi/v2-3/maple/v202.mpl"):

> with(plots):

Kartion massakeskip. Gaussilla

>

> x:=r*cos(Theta): y:=r*sin(Theta):

> plot3d([x,y,r],r=0..2,Theta=0..2*Pi,axes=box);

> x:='x': y:='y':

> a2:=x->-sqrt(4-x^2); b2:=-a2;

> a3:=(x,y)->sqrt(x^2+y^2); b3:=(x,y)->2;

> Int(Int(Int(sqrt(x^2+y^2),z=a3(x,y)..2),y=a2(x)..b2(x)),x=-2..2);

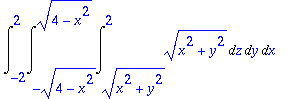
> #evalf(%);

Warning, computation interrupted

> # %=evalf(value(%)); # kestää liian kauan.

> Digits:=12:gtaulu:=gausstaulukko(5):

> f:=(x,y,z)->sqrt(x^2+y^2);

> Gaussxyz(gtaulu,gtaulu,gtaulu,f,-2,2,a2,b2,a3,b3);

> gtaulu:=gausstaulukko(10):

> 10^3;

> Gaussxyz(gtaulu,gtaulu,gtaulu,f,-2,2,a2,b2,a3,b3);

> 15^3;

> gtaulu:=gausstaulukko(15):

> Gaussxyz(gtaulu,gtaulu,gtaulu,f,-2,2,a2,b2,a3,b3);

> gtaulu:=gausstaulukko(20):

> 20^3;

> Gaussxyz(gtaulu,gtaulu,gtaulu,f,-2,2,a2,b2,a3,b3);

Lasketaan sylinerikoord:

> Int(Int(Int(r*r,z=r..2),r=0..2),Theta=0..2*Pi);

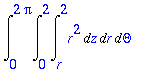
> value(%);

> evalf(%);

> gtaulu:=gausstaulukko(5): 5^3;

> Gaussxyz(gtaulu,gtaulu,gtaulu,(Theta,r,z)->r^2,0,2*Pi,0,2,(Theta,r)->r,2);

Huom! Gaussxyz:n parametrilistassa olevissa funktiomäärityksissä argumenttien on oltava samassa järjestyksessä

kuin yllä integraalissa (eli 1. muuttuja vastaa 1. rajoja (a1,b1), jne.)

Huomataan, että siirtyminen lieriökoordinaatteihin paransi numeerisen laskennan tarkkuutta olennaisella tavalla.

Voidaan jatkaa tästä laskemalla momentit. Ehkäpä harjoitustehtäväksi jatko.

> #?Int[numerical]

> eint:=evalf@Int;

> eint(Int(x*y,x=0..1),y=0..1);

> Gaussxy(gtaulu,gtaulu,(x,y)->x*y,0,1,0,1);

>

>