Numeerista integrointia, osa 2, L/numint2.mws

V2/2002, 17.2.02 HA

Alustukset

> restart:

Warning, the name changecoords has been redefined

> #read("c:\\opetus\\maple\\v202.mpl"):

> #read("/p/edu/mat-1.414/maple/v202.mpl"):

> read("/home/apiola/opetus/peruskurssi/v2-3/maple/v202.mpl"):

Muutettiin vähän tyyliä. Otetaan sittenkin gausstaulukko parametrilistaan, eikä käytetä globaalia. Vaihdetaan nimi isolla G:llä alkavaksi (vanhakin on tallella.)

Tässä koko arsenaali:

> op(gausstaulukko);op(gaussolmut); op(gausspainot);op(Gaussint);

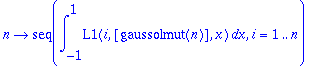
> Gaussint(gausstaulukko(3),cos); #"Kertakäyttötapa" pienellä n:llä.

> int(cos(x),x=-1..1): evalf(%);

Integrointi mielivaltaisen välin yli, testausta

Otetaan mukaan muuttujanvaihto, jolla saadaan integrointi mieleivaltaisen välin [a,b] yli:

> Gaussab:=(taulu,f,a,b)->Gaussint(taulu,t->f(1/2*t*b-1/2*t*a+1/2*b+1/2*a)*(1/2*b-1/2*a));

Testataan:

> Gaussab(gausstaulukko(3),cos,-1,1);

> Gaussab(gausstaulukko(3),cos,-2,2);

> int(cos(x),x=-2..2): evalf(%);

Esim:

> int(4/(1+x^2),x=0..1);

> f:=x->4/(1+x^2);

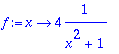
> n:=2: gtaulu2:=gausstaulukko(n):n:=4: gtaulu4:=gausstaulukko(n):n:=8: gtaulu8:=gausstaulukko(n):

> Gaussab(gtaulu2,f,0,1);

> Gaussab(gtaulu4,f,0,1);

> Gaussab(gtaulu8,f,0,1);

Entä, jos jaetaan väli [0,1] kahteen osaan, joilla kummallakin sovelletaan 4:n pisteen Gaussia:

> Gaussab(gtaulu4,f,0,1/2)+Gaussab(gtaulu4,f,1/2,1);

> evalf(Pi);

9:nnessä numerossa on eroa (4:n verran), "globaali" on tässä esimerkissä senverran parempi. Sietää tutkia lisää.

Tasointegraali ja avaruusintegraali

Tästä aiheesta ei ole KRE-kirjassa (muista "oppikirjoistamme" puhumattakaan) mitään. Tärkeimmät lähteemme:

[KMN] Kahaner-Moler-Nash: Numerical Methods and Software

[Rec] Press-Flannery-Teukolski-Vetterling: Numerical Recipes, The Art of Scientific Computing

[BF] Burden-Faires: Numerical Analysis

Tehtävä on merkittävästi vaikeampi kuin 1 muutt, fkt.

• 1) Jos funktion arvoja on laskettava R:ssä n kpl., niin R^ 3:ssa luokkaa n^3, jotta päästäsiiin samaan tarkkuteen. (Esim n=30 -> n^3 = 27 000 )
• 2) Integrointijoukon geometria voi olla monimutkainen.
• Jos alueen reuna on monimutkainen, mutta integroitava ei sisällä teräviä piikkejä, mutta saa muuten olle "epäsileä", ja tarkkuusvaatimus ei ole suuri (jokunen prosentti), niin

Monte-Carlo on hyvä ehdokas.

Jos reuna on sileä ja yksinkertainen ja funktio on sileä, niin peräkköiset 1-ulotteiset integraalit toimivat.

Lukuteoreettiset menetelmät: Jokunen sana tuonnempana.

Funktion ja alueen luonteesta riippuen on paikallaan toisinaan jakaa alue eri osiin ja laskea integraalit yhteen. (Adaptiivinen algoritmi, mutta toisinaan on mahdotonta

automatisoida, tarvitaann käsityötä.

Kirjoitetaan ensin integrointi yli yksikköneliön. Muutetaan gaussintnelio iso-G-alkuiseksi (ja lyhennetään vähän nimeä). Siinä taas siirretään aiemmat globaalit parametriilistaan.

> op(Gaussnelio);

> gtaulux:=gausstaulukko(3);gtauluy:=gausstaulukko(4):

> Gaussnelio(gtaulux,gtauluy,(x,y)->x^5*y^7);

> m:=3: n:=4: d1:=2*m-1; d2:=2*n-1;

> Gaussnelio(gtaulux,gtauluy,(x,y)->x^d1*y^d2);

> int(int(x^d1*y^d2,x=-1..1),y=-1..1): evalf(%);

Tämä ei merkitse, että mikä tahansa astetta 12 oleva kahden muuttujan polynomi integroituisi tarkasti. Jos vaikka d1:een lisätään 1 ja d2:sta vähennetään 1, niin mikään

ei enää takaa, että integroituminen olisi tarkkaa (koska x-puolella ylitettiin tarkan integroituvuuden asteluku).

Tiedetään vain, että kaikki astelukua d=min{d1,d2} olevat 2:n muuttujan polynomit integroituvat tarkkaan ja lisäksi eräät korkeampiasteiset, kuten x^d1 y^d2

> Gaussnelio(gtaulux,gtauluy,(x,y)->x^(d1+1)*y^(d2-1)),int(int(x^(d1+1)*y^(d2-1),x=-1..1),y=-1..1): evalf(%);

> Gaussnelio(gtaulux,gtauluy,(x,y)->x^4*y^4),int(int(x^4*y^4,x=-1..1),y=-1..1): evalf(%);

> Gaussnelio(gtaulux,gtauluy,(x,y)->x^5*y^6),int(int(x^5*y^5,x=-1..1),y=-1..1): evalf(%);

> Gaussnelio(gtaulux,gtauluy,(x,y)->x^6*y^6),int(int(x^6*y^6,x=-1..1),y=-1..1): evalf(%);

> Gaussnelio(gtaulux,gtauluy,(x,y)->x^6*y^6),int(int(x^6*y^6,x=-1..1),y=-1..1): evalf(%);

Nyt voitaisiin tehdä muunnos integroitavalta alueelta yksikköneliölle ja palauttaa integraali sillä tavoin tähän. Ehkäpä otetaan harjoituksen aiheeksi.

Seuraavassa suoritetaan peräkkäiset integroinnit ensin x-projisioituvalle tasoaluleelle ja sitten xy-projisioituvalle avaruuskappaleelle.

Siinä emme käytä Gaussnelio-funktiota, vaan rakennamme Gaussab :n varaan.

Tasointegraali peräkkäisinä integraaleina

> a2:=x->-sqrt(1-x^2);b2:=-a2;

> gtaulux;f:=(x,y)->1;

> F:=x->Gaussab(gtauluy,f,a2(x),b2(x));

> F(0.5);

> Gaussab(gtaulux,F,-1,1);

Mahtava juttu, nyt Maple tottelee ihan normaalia matematiikkaa!

> Gaussxy:=(gtaulux,gtauluy,f,a1,b1,a2,b2)->Gaussab(gtaulux,x->Gaussab(gtauluy,y->f(x,y),a2(x),b2(x)),a1,b1);

> gtaulux:=gausstaulukko(3):

> Gaussxy(gtaulux,gtaulux,(x,y)->x^2*y^2,-1,1,a2,b2);

> n:=5: gtaulux:=gausstaulukko(n): Gaussxy(gtaulux,gtaulux,1,-1,1,x->-sqrt(1-x^2),x->sqrt(1-x^2));

> for n from 3 to 15 do gtaulux:=gausstaulukko(n): ala[n]:=Gaussxy(gtaulux,gtaulux,1,-1,1,x->-sqrt(1-x^2),x->sqrt(1-x^2)): od:

>

> seq(ala[n],n=3..15);

Avaruusintegraali peräkkäisinä integraaleina

Nyt homma osataan. Kyse on vain siitä, tehdäänkö pitkä "one-liner" vai pari lyhyempää riviä.

Laskettavana on

> restart: Int(Int(Int(f(x,y,z),z=a3(x,y)..b3(x,y)),y=a2(x)..b2(x)),x=a1..b1);

Warning, the name changecoords has been redefined

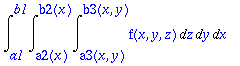
> read("/home/apiola/opetus/peruskurssi/v2-3/maple/v202.mpl"):

>

> # G:=(x,y)->Gaussab(gtaulux,z->f(x,y,z),a3(x,y),a2(x,y)); # Tämä on kehittelyä.

> Gaussxyz:=(gtaulux,gtauluy,gtauluz,f,a1,b1,a2,b2,a3,b3)->Gaussxy(gtaulux,gtauluy,(x,y)->Gaussab(gtauluz,z->f(x,y,z),a3(x,y),b3(x,y)),a1,b1,a2,b2);

Houkutus one-lineriin oli liian suuri!

> a3:=(x,y)->x-y: b3:=(x,y)->x+y:

> Int(Int(Int(z,z=a3(x,y)..b3(x,y)),y=x^2..x),x=0..1): %=evalf(value(%));

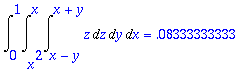
> gtaulux:=gausstaulukko(5):

>

> Gaussxyz(gtaulux,gtaulux,gtaulux,(x,y,z)->z,0,1,x->x^2,x->x,a3,b3);

>

Eipä huono ensimmäiseksi testiksi!