Numeerista integrointia, L/numint1.mws

V2/2002, viimeinen viikko 16.2.02 HA

Alustukset

> restart:

Warning, the name changecoords has been redefined

> #read("c:\\opetus\\maple\\v202.mpl"):

> #read("/p/edu/mat-1.414/maple/v202.mpl"):

> read("/home/apiola/opetus/peruskurssi/v2-3/maple/v202.mpl"):

> #op(L);

> op(L1);

> seq(L1(i,[x1,x2,x3],x),i=1..3);

Kertausta: Lagrangen interpolaatio

Lagrangen interpolaatiomenetelmässä muodostetaan annettuun xdataan [x0,...,xn] liittyvät polynomit L[0],...,L[n], siten että

L[i](x[j])=delta[i,j]

> L:='L': L[i](x[j])=delta[i,j];

> xd:=[x0,x1,x2,x3];

> read("/home/apiola/opetus/peruskurssi/v2-3/maple/v202.mpl"):

> L(0,xd,x);

> L(1,xd,x);

jne. Yleisesti: KRE s. 849 Lagrange interpolation.

Lagrangen (kertoja)polynomit on valmiina koodattu tiedostossamme v202.mpl , joka luettiin yllä. Siksi nuo kaavatkin tulivat

yllä ihan oikein, kun vaan tarjottiin L-kirjainta!

Lagrangen polynomien avulla voidaan kirjoittaa suoraan yleinen interpolaatiotehtävän ratkaisu:

Tehtävä:

Annettu xdata=[x0,...,.xn] ja ydata=[y0,..,yn]. Määrättävä korkeintaan astetta n oleva polynomi näiden datapisteiden

kautta.

Tiedämme, että polynomin kertoimet saataisiin ratkaisemalla lineaarinen yhtälösysteemi, jonka kerroinmatiirina on Vandermonden matriiisi. Kuten PNS:n yhteydestä muistamme, Vandermonde on ei-singulaarinen ja tässä tapauksessa

neliömatriisi, joten 1-käs ratkaisu on.

Tätä tietoa emme tarvitse Lagrangen menetelmässä, emme myöskään joudu ratkaisemaan yhtälösysteemiä, vaan nerokkuus

piilee Lagrangen polynomien ortogonaalisuustyyppisessä ominaisuudessa (kts. yllä).

Ratkaisu:

> L:='L':

> 'p(x)'=sum(y[i]*L[i](x),i=0..n);

Jäännöstermille voidaan johtaa lauseke:

> R=product((x-x[i]),i=0..n)*D[n+1](f)(xi)/n!;

Tällöin käytettävissä on funktio (n+1) kertaa derivoituva funktio f, jonka arvot x-datapisteissä ovat y-data-arvoja:

> y[i]=f(x[i]), i=0..n;

>

Kertausta : Gaussin integrointi 1-dim tapaus

Erilaisia integrointisääntöjä "quadrature rules" saadaan integroimalla interpolaatiopolynomeja.

Ensimmäiseksi mieleen juolahtava ajatus on jakaa väli tasavälisesti ja muodostaa interpolaatiopolynomi, joka integroidaan.

Näin saadaan ns. Newton-Cotes-kaavat. Kaksi alinta astetta olevaa Newton-Cotes-kaavaa ovat trapetsisääntö (puolisuunnikas-) ja

Simpsonin sääntö. Niissä approksimidaan pinta-alaa puolisuunnikkaalla ja vastaavasti 2. asteen polynomin reunustamalla alalla.

Yhdistetyt säännöt: ("Composite rules")

Alhaista kertalukua olevilla kaavoilla laskettaessa jaetaan koko integroimisalue osiin, joilla kullakin sovelletaan ao. sääntöä. Koko integraali on osien summa.

Optimaalinen solmujen valinta, Gaussin säännöt.

Yleisemmin voidaan valita mikä tahansa (ei välttämättä tasavälinen) pisteistö x1,...,xn integrointiväliltä [a,b].

Huom! Vaihdoimme indeksoinnin alkamaan 1:stä, tämä korostaa sitä, että johtamisen alaisena olevat kaavat ovat yleensä ns. " avoimia kaavoja" ,

joissa s olmupisteet x[i] ovat välin sisäpisteitä.

> L:='L':n:='n':p:=sum(y[i]*L[i](x),i=1..n);

> intsaanto:=sum(f(x[i])*Int(L[i](x),x=a..b),i=1..n);

Merk:

> w[i]=Int(L[i](x),x=a..b);

> intsaanto:=sum(w[i]*f(x[i]),i=1..n);

Yleisesti saadaan painotettu summa funktion arvoista.

Gaussin idea: Annetaan solmujen x[i] olla muuttujina optimointitehtävässä:

Valitse solmut x[i] ja painot w[i] siten, että integrointisääntö on tarkka mahdollisimman korkea-asteisilla polynomeilla.

Korkein asteluku, joka voidaan toivoa saavutettavaksi, on 2n-1 (2n tuntematonta, 2n määrättävää kerrointa).

Ratkaisutapa 1: Muodostetaan (epälineaarinen) yhtälösysteemi integroimalla monomeja 1,x,x^2, ... .

Tällä saadaan alhaista kertalukua olevia (ainakin n=2). Korkeampia voidaan yrittää vaikka Newtonin menetelmällä

ratkaista, mutta se ei johda pitkälle.

Ratkaisutapa 2: Normeerataan integrointi välille [-1,1]. Osoittautuu, että solmut x1,...,xn saadaan ns. Legendren

polynomien nollakohtina. Kun solmut tunnetaan, saadaan painot yksinkertaisesti kaavasta:

> w[i]=Int(L[i](x),x=-1..1);

Integrointi yleisen välin [a,b] yli hoituu yksinkertaisella lineaarisella muuttujanvaihdolla. (Nokkelia kun ollaan,

niin muodostetaan 1. asteen interpolaatiopolynomi, joka a:ssa saa arvon -1 ja b:ssä arvon 1.)

> read("/home/apiola/opetus/peruskurssi/v2-3/maple/v202.mpl"):

> (-1)*L(0,[a,b],x)+1*L(1,[a,b],x);simplify(%);

> t:='t':

> tyht:=t=%%;

> xx:=solve(%,x);

> dx:=diff(xx,t);

Saadaan integrointikaava:

> Int(f(x),x=a..b)=Int(f(xx)*dx,x=-1..1);

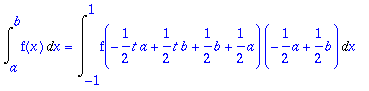
Maple-toteutus

> with(orthopoly);

Warning, the name L has been redefined

> #read("c:\\opetus\\maple\\v202.mpl"):

Varusta read-käsky kommentilla ja mene alkuun suorittamaan asianmukainen read.

> read("/home/apiola/opetus/peruskurssi/v2-3/maple/v202.mpl"): # Nimikonflikti on lähellä, emme kuitenkaan tarvitse polynomia L - Laguerren polynomi, vaan Legenren polynomia, jonka Maplen orthopoly nimeää P:ksi.

( L-matemaatikoita riittää: Lagrange, Legendre, Laguerre, Laplace, ... )

Gaussin integroinnin yhteydessä on tapana indeksoida Lagrangen polynomit (siis solmut) 1..n. Siis datapisteitä on

n kpl, jolloin interpoloidaan n-1 asteisella polynomilla. Tavoitteena siis kaava, joka on tarkka asteeseen 2n-1 saakka.

Jatkon indeksipeliä helpottaa, kun kirjoitamme Lagrangen kertojapolynomista version L1, jossa indeksointi menee

1..n. (Koodikin on hiukan yksinkertaisempi.)

> op(L1);

>

> P(10,x);

> Digits:=15:

> fsolve(P(10,x)=0,x);

> Digits:=10:

> gausssolmut:=seq([fsolve(P(k,x)=0,x)],k=1..5);

> %[2,1];

Näin voitaisiin muodostaa riittävän iso taulukko, josta haettaisiin solmut. Järkevää olisi kirjoittaa taulukko tiedostoon, josta solmut luettaisin, ainakin, jos

haluttaisiin varautua isoon taulukkoon.

Ohjelmoinnin kannalta on kätevämpää tehdä pari pikku funktiota, joista kasataan varsinainen integrointifunktio.

Joka tapauksessa kannattaa tehdä erikseen solmujen ja painojen laskenta, jotta niitä ei tarvitse laskea kuin kerran tietyn kertaluvun menetelmää kohti.

Ohjelmointi on äärimmäisen yksinkerttaista.

> gaussolmut:=k->fsolve(P(k,x)=0,x);

> L1(3,[a,b,c],x);

> gausspainot:=n->seq(int(L1(i,[gaussolmut(n)],x),x=-1..1),i=1..n);

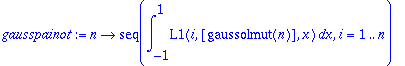
> gausspainot(3);

> gausstaulukko:=n->[[gaussolmut(n)],[gausspainot(n)]];

> gausstaulukko(10);

> sw:=gausstaulukko(4);

> gaussint:=proc(n,f)
# Suorita ensin gtaulu:=gausstaulukko(n);
global gtaulu;
local s,w,i;
s:=gtaulu[1]; w:=gtaulu[2];
sum(w[i]*f(s[i]),i=1..n);
end:

>

> gtaulu:=gausstaulukko(3);

> gaussint(3,x->x^4),int(x^4,x=-1..1); evalf(%);

> n:=3: gtaulu:=gausstaulukko(n):

> seq([gaussint(3,x->x^k),evalf(int(x^k,x=-1..1))],k=1..2*n-1);

Astetta 5=2n-1 olevaan saakka kaava integroi polynomit tarkkaan (pyöristystä vaille). Arvolla 2n tulee jo selkeä ero.

> gaussint(3,x->x^(2*n)),evalf(int(x^(2*n),x=-1..1));

Integrointi yli neliön

> gaussintnelio:=proc(m,n,f)
# Suorita ensin gtaulux:=gausstaulukko(m);
# gtauluy:=gausstaulukko(n);
global gtaulux,gtauluy;
local sx,wx,sy,wy,i,j;
sx:=gtaulux[1]; wx:=gtaulux[2];
sy:=gtauluy[1]; wy:=gtauluy[2];
sum(wx[i]*sum(wy[j]*f(sx[i],sy[j]),j=1..n),i=1..m);
end:

> gtaulux:=gausstaulukko(3);

> gtauluy:=gtaulux:

> gaussintnelio(3,3,(x,y)->x^4*y^4),int(int(x^4*y^4,x=-1..1),y=-1..1); evalf(%);

> sx:=gtaulux[1]:sy:=gtauluy[1]:

> with(plottools): with(plots):

Warning, the name arrow has been redefined

Warning, the name arrow has been redefined

> n:=3:

> nelio:=polygon([[1,1],[-1,1],[-1,-1],[1,-1]]):

> ss:=seq(seq([sx[i],sy[j]],j=1..n),i=1..n):

> display(nelio,plot([ss],style=point),axes=frame);

>

>