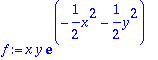
Kriittiset pisteet, min/max
12.3.02
> restart:
Warning, the name changecoords has been redefined
> with(linalg): with(LinearAlgebra): with(plots):
Warning, the protected names norm and trace have been redefined and unprotected
Warning, the assigned name GramSchmidt now has a global binding
> setoptions3d(axes=boxed,orientation=[-30,50]):
Esim
> f:=x*y*exp(-(x^2+y^2)/2);
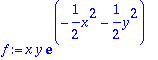
> f1:=diff(f,x);f2:=diff(f,y);
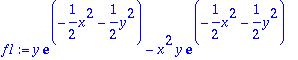
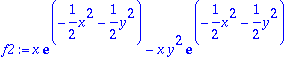
> f11:=diff(f1,x);
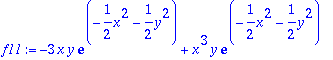
> f12:=diff(f1,y): f12:=simplify(%);
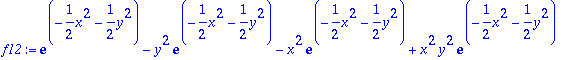
> factor(%);
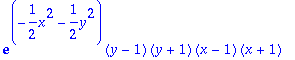
> f22:=diff(f2,y);factor(%);
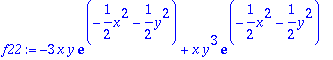
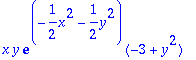
> solve({f1=0,f2=0},{x,y});
![]()
> H:=<<f11,f12>|<f12,f22>>:
> H00:=subs(x=0,y=0,H);
![H00 := _rtable[136594488]](images/minmax10.gif)
> Eigenvalues(H00);
![_rtable[134654764]](images/minmax11.gif)
> H11:=subs(x=1,y=1,H),piste=[1,1];Hm11:=subs(x=-1,y=1,H),piste=[-1,1];Hm1m1:=subs(x=-1,y=-1,H),piste=[-1,-1];H1m1:=subs(x=1,y=-1,H),piste=[1,-1];
![H11 := _rtable[134935360], piste = [1, 1]](images/minmax12.gif)
![Hm11 := _rtable[135374044], piste = [-1, 1]](images/minmax13.gif)
![Hm1m1 := _rtable[137310240], piste = [-1, -1]](images/minmax14.gif)
![H1m1 := _rtable[137454396], piste = [1, -1]](images/minmax15.gif)
Pisteet (1,1) ja (-1,-1) ovat max (neg. def.), pisteet (1,-1) ja (-1,1) ovat min (pos. def.)
> plot3d(f,x=-2..2,y=-2..2);
![[Maple Plot]](images/minmax16.gif)
> plot3d(f,x=-4..4,y=-4..4);
![[Maple Plot]](images/minmax17.gif)
Esimerkki 3:n muutt. fkt:sta
> f:=x^2*y+y^2*z+z^2-2*x;
![]()
> KRPyht:={diff(f,x)=0,diff(f,y)=0,diff(f,z)=0};
![]()
> solve(KRPyht,{x,y,z});
![]()
![]()
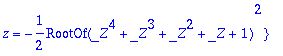
> map(allvalues,[%]);
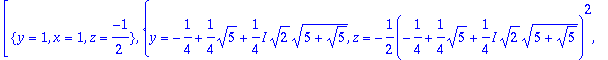
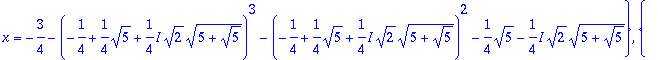
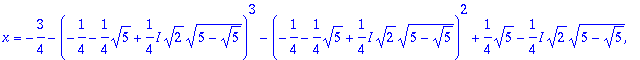
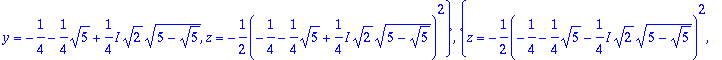
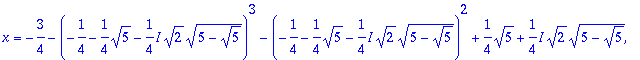
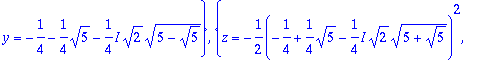
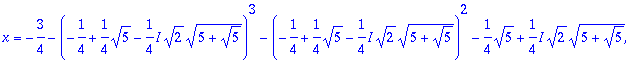
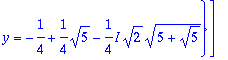
> %%[1];
![]()
Tämä on ainoa reaalijuuri.
> H:=Matrix(hessian(f,[x,y,z]));
![H := _rtable[137384468]](images/minmax32.gif)
> Hp:=subs(y = 1, x = 1, z = -1/2,H);
![Hp := _rtable[137382684]](images/minmax33.gif)
> Eigenvalues(Hp);evalf(%);
![_rtable[137293984]](images/minmax34.gif)
![_rtable[137294064]](images/minmax35.gif)
Satulapiste. 1. ja 3. tai 2. ja 3. muodostavat satula-akseliparin.
> ff:=unapply(f,x,y,z);
![]()
> plot3d(ff(x,1,z),x=0..2,z=-1..0,labels=[x,z,'f'],title="xz-tason suunnassa");
![[Maple Plot]](images/minmax37.gif)
> plot3d(ff(1,y,z),y=0..2,z=-1..0,title="yz-tason suunnassa");
![[Maple Plot]](images/minmax38.gif)
Nähdään: 1) Jos pidetään y:llä kiinteä arvo y=1 ja liikutaan siis xz-tason suuntaan KRP:stä, niin f kasvaa.
2) Jos pidetään x:llä kiinteä arvo x=1 ja liikutaan yz-tason suuntaan KRP:stä, niin f pienenee.
Siispä todellakaan f:llä ei ole ääriarvoa KRP:ssä
KRP-yhtälön ratkaisu numeerisesti
Todellisuudessa KRP-yhtälösysteemin ratkaisu onnistuu vain harvoin analyyttisesti. Numeerisen ratkaisijan fsolve käyttö vaatii alkuarvojen tunnustelemista. 2 muuttujan tapauksessa piirtely on suureksi avuksi. Tässä vähän vihjettä
> #f:=(x,y)-> ...;g:=Vector(grad(f(x,y),[x,y]));
> H:=Matrix(hessian(f(x,y),[x,y])):
> KRPyht:=g[1]=0,g[2]=0:
> display(implicitplot(g[1]=0,x=0.5..2,y=0.5..2),implicitplot(g[2]=0,x=0.5..2,y=0.5..2,color=blue)):
Kannattaa valita hiirellä alkuarvoja, jotka voi antaa fsolvelle tyylin:
> KRPa:=fsolve({KRPyht},{x=xa,y=ya});
>