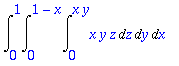
L/int23d.mws

7.4.02 HA

Alustukset

> restart:

Warning, the name changecoords has been redefined

> with(plots):

> with(plottools):

> setoptions3d(axes=boxed,orientation=[-30,50]):

> #read("/home/apiola/opetus/peruskurssi/v2-3/maple/v202.mpl");

Luento ti 9.4.02

Avaruusintegraalin laskeminen [LP] s. 173, [VA] s. 132, [Ad] s. 851 .

Esim1) Laskettava:

> Int(Int(Int(x*y*z,z=0..x*y),y=0..1-x),x=0..1);

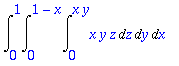
Käsin laskettaessa riittää useimmiten piirtää kappaleen projektio xy-tasoon (xy-projisioituvassa tapauksessa).

Kuvan piirto on tietysti asiaa havainnollistava. Maplella se onnistuu mainiosti. Kuvan piirto Maplella on aivan samanlainen tehtävä kuin integroimisrajojen määrääminen. Siten nämä tehtävät tukevat hyvin toisiaan.

(Erityinen kiitos Maplen plot3d: n suunnitelijoille!)

Projektio saadaan tässä ihan perusplotilla:

> plot(1-x,x=0..1);

Nyt se 3d-kuva:

> suoraseina:=plot3d([x,1-x,z],x=0..1,z=0..x*(1-x),labels=[x,y,z]):

> display(suoraseina,plot3d(x*y,x=0..1,y=0..1-x),style=patchcontour);

Käsin laskien luennolla muotoon:

> Int(x*Int(y*(x*y)^2/2,y=0..1-x),x=0..1): %=value(%);

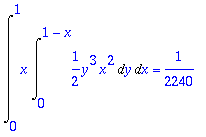
> Int(Int(Int(x*y*z,z=0..x*y),y=0..1-x),x=0..1): %=value(%);

>

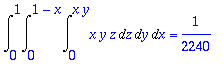
Esim. 2

> plot([2*cos(Theta),2*sin(Theta)-1,Theta=0..2*Pi],scaling=constrained);

> solve(r^2+2*r*sin(Theta)-3=0,r); R:=%[1]; # Voi vaihdella eri ajokerroilla.

>

> x:=r*cos(Theta): y:=r*sin(Theta):

> taso:=plot3d([x,y,3-2*y],Theta=0..2*Pi,r=0..R,labels=["x","y","z"]):

> taso;

> paraboloidi:=plot3d([x,y,r^2],Theta=0..2*Pi,r=0..R,labels=["x","y","z"]):paraboloidi;

> display(taso,paraboloidi,style=patchcontour);

> Int((3-2*r*sin(Theta)-r^2)*r,r=0..-sin(Theta)+sqrt(sin(Theta)^2+3));

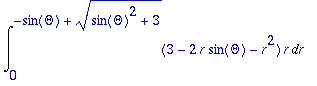
> value(%);

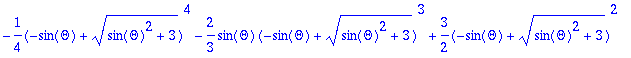
> rint:=%:

> vV:=int(rint,Theta=0..2*Pi);

Komeasti Maple sen osasi! Katsotaan, miltä näyttää integraalifunktio:

> int(rint,Theta);

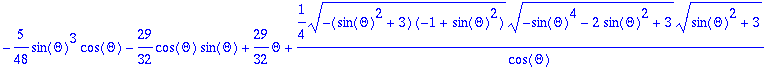
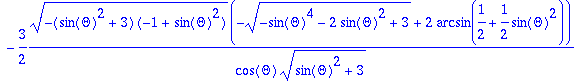
> simplify(%);

Eipä tuosta käsin laskien selviäisi!

Oliskohan muuten mennyt helpommin ilman napakoordinaattimuunosta?

Kannattaa kokeilla! No tehdään.

> x:='x': y:='y': z:='z':

Tarkistetaan ensin, että rajat tulivat oikein:

> plot3d([x,y,0],x=-2..2,y=-1-sqrt(4-x^2)..-1+sqrt(4-x^2),view=[-2..2,-3..1,-1..1],grid=[50,50],color=red,style=patchnogrid);

Tähän saakka tehtiin käsin taululla:

> Int(Int(3-2*y-x^2-y^2,y=-1-sqrt(4-x^2)..-1+sqrt(4-x^2)),x=-2..2);

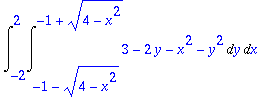
> Int(int(3-2*y-x^2-y^2,y=-1-sqrt(4-x^2)..-1+sqrt(4-x^2)),x=-2..2);

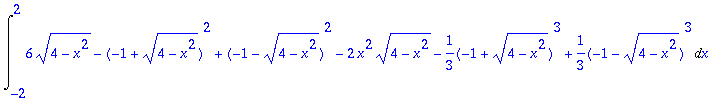
> value(%);

> Int(simplify(int(3-2*y-x^2-y^2,y=-1-sqrt(4-x^2)..-1+sqrt(4-x^2))),x=-2..2);

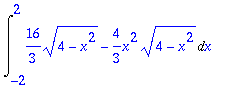
> infolevel[int]:=3:

> value(%%);

int/elliptic:   trying elliptic integration

int/indef1:   first-stage indefinite integration

int/indef1:   first-stage indefinite integration

int/indef1:   first-stage indefinite integration

> infolevel[int]:=0: # Takaisin normaalitilaan!

Eikö nyt parempaa muuttujanvaihtoa löydy?

Katsotaanpa, miten piirsimme aivan ensimmäisen kuvan. Projektiokiekko piirrettiin ottamalla origoksi piste (0,-1) ja sitten vain siirrettiin.

No jospa siirretään takaisinpäin.

Ts. muunnos:

          u = x        <==>       x=u
          v=y+1                   y=v-1

Tällöin Jakobin det = 1

> c1:=(u,v)->u^2+(v-1)^2; c2:=(u,v)->3-2*(v-1);

> Int(Int(c2(r*cos(Theta),r*sin(Theta))-c1(r*cos(Theta),r*sin(Theta))*r,r=0..2),Theta=0..2*Pi);

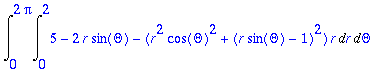
> value(%);

Näinpä tämä muuttui puhtaaksi käsinlaskuksi.

>