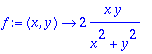
Raja-arvot ja jatkuvuus
Luento 12.2.02 HA
Esim, jossa raja-arvoa ei ole.
>
zoom:=(f,x0,y0,w)->plot3d(f(x,y),x=x0-w/2..x0+w/2,y=y0-w/2..y0+w/2,axes=BOX):
# Esim: f:=(x,y)->x*y; zoom(f,0,0,1);zoom(f,0,0,1/2);zoom(f,0,0,1/4);
> f:=(x,y)->2*x*y/(x^2+y^2);
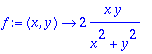
> w:=1:
> zoom(f,0,0,w); w:=w/2: # Toista tätä!
![[Maple Plot]](images/Limes2.gif)
> zoom(f,0,0,w); w:=w/2:
![[Maple Plot]](images/Limes3.gif)
> zoom(f,0,0,w); w:=w/2:
![[Maple Plot]](images/Limes4.gif)
> w:=w/100;
![]()
> zoom(f,0,0,w);
![[Maple Plot]](images/Limes6.gif)
Laatikon pystyreunan pituus on 2
![]() kaikissa kuvissa, vaikka deltaa pienennetään kuinka.
kaikissa kuvissa, vaikka deltaa pienennetään kuinka.
Tämä näyttää, että deltaa pienentämällä ei saada funktion arvoja 2:ta matalamman lieriön sisään.
Kokeellisesti nähdään, että raja-arvoa ei varmastikaan ole. (Tämä ei ole matemaattinen todistus, vaan vakuuttava havainnollistus.)
> with(plots):
> implicitplot(f(x,y)=0.5,x=-1..1,y=-1..1);
![[Maple Plot]](images/Limes8.gif)
> contourplot(f(x,y),x=-1..1,y=-1..1,contours=[.1,.2,.5,1]);
![[Maple Plot]](images/Limes9.gif)
> f(x,y);
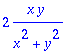
> densityplot(f(x,y),x=-1..1,y=-1..1);
![[Maple Plot]](images/Limes11.gif)
Tämä on varsin luotettava funktio. (Ruutu saa sitä vaaleamman värin, mitä korkeampi arvo funktiolla on.)
>
Esimerkki raja-arvosta (jatkuvuudesta)
> f:=(x,y)->2*x*y/sqrt(x^2+y^2);
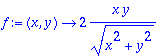
> w:=1:
> zoom(f,0,0,w); w:=w/2:
![[Maple Plot]](images/Limes13.gif)
> zoom(f,0,0,w); w:=w/2:
![[Maple Plot]](images/Limes14.gif)
> zoom(f,0,0,w); w:=w/2:
![[Maple Plot]](images/Limes15.gif)
> zoom(f,0,0,w); w:=w/2:
![[Maple Plot]](images/Limes16.gif)
> densityplot(f(x,y),x=-1..1,y=-1..1);
![[Maple Plot]](images/Limes17.gif)
> implicitplot(f(x,y)=.3,x=-1..1,y=-1..1);
![[Maple Plot]](images/Limes18.gif)
>
>
Esim, jossa säteittäiset raja-arvot=0, silti ei raja-arvoa
> f:=(x,y)->2*x^2*y/(x^4+y^2);
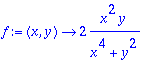
> plot([seq(f(x,k*x),k=[.5,1,2])],x=-1..1,color=[red,green,blue]);
![[Maple Plot]](images/Limes20.gif)
> sateella:=k->spacecurve([x,k*x,f(x,k*x)],x=-1..1,color=blue,thickness=3);sateella0:=k->spacecurve([x,k*x,0],x=-1..1,color=blue,thickness=3);
![]()
![]()
> paraabelilla:=k->spacecurve([x,k*x^2,f(x,k*x^2)],x=-1..1,color=red,thickness=2);para0:=k->spacecurve([x,k*x^2,0],x=-1..1,color=red,thickness=2);
![]()
![]()
> plot3d(f(x,y),x=-1..1,y=-1..1,axes=box);
![[Maple Plot]](images/Limes25.gif)
> sateella(1);
![[Maple Plot]](images/Limes26.gif)
> display(%,%%);
![[Maple Plot]](images/Limes27.gif)
> display(%,sateella0(1));
![[Maple Plot]](images/Limes28.gif)
> display(%,paraabelilla(1),para0(1));
![[Maple Plot]](images/Limes29.gif)
Sama uudelleen, mutta "hallitummin".
> pintakuva:=plot3d(f(x,y),x=-1..1,y=-1..1,axes=box):
> sadekuva:=display(sateella(1),sateella0(1)):
> parakuva:=display(paraabelilla(1),para0(1)):
> display(pintakuva,sadekuva,parakuva);
![[Maple Plot]](images/Limes30.gif)
> display(%,style=wireframe);
![[Maple Plot]](images/Limes31.gif)
Alempi punainen on paraabeli xy-tasossa ja ylempi näyttää funktion arvot tällä paraabelilla.
Suora sininen on säde xy-tasossa, käyrä sininen näyttää funktion arvot tällä säteellä.