Harj. 8 LV

22.3.2002 HA ja JP

Alustukset

> restart:

Warning, the name changecoords has been redefined

> with(LinearAlgebra):with(linalg):with(plottools): with(plots):setoptions3d(axes=boxed,orientation=[-30,50]):

Warning, the previous binding of the name GramSchmidt has been removed and it now has an assigned value

Warning, the protected names norm and trace have been redefined and unprotected

Warning, the name arrow has been redefined

Warning, the name arrow has been redefined

> V2L:=vek->convert(vek,list):

1.

Tämä on puhtaasti vanhan kertausta. Tämä nyt lähinnä siksi, ettei kaikki ole kahden muuttujan tapauksia. Samalla harjaannutaan Maple-työskentelyssä tutun teeman parissa.

> f:=(x,y,z)->4*x*y*z-x^4-y^4-z^4;

> g:=grad(f(x,y,z),[x,y,z]);

> solve({g[1]=0,g[2]=0,g[3]=0},{x,y,z});

> H:=Matrix(hessian(f(x,y,z),[x,y,z]));

> H111:=subs(x=1,y=1,z=1,H);

> Eigenvalues(H111);

Ominaisarvot ovat kaikki negatiivisia, joten kyseessä on negatiivisesti definiitti matriisi ja (1,1,1) on maksimipiste.

Huom! Kirjallisuudessa esiintyy diagonaalialideterminanttien avulla lausuttavia ehtoja.

Niitä ei tarvitse osata. (Jos joku soveltaa niitä oikein, niin ok, mutta en kehoita opettelemaan.)

Ominaisarvojen merkit kertovat syyn asioiden tilaan, siksi niitä suosin vahvasti.

Koetehtävissä ei tule olemaan mitään laskennallista etua determinanttiehtojen osaamisesta.

2.

> q:=3*x^2+2*x*y + 3*y^2;

> A:=<<3,1>|<1,3>>;

> det(A);

Ominaisarvot ovat samanmerkkiset, merkki on sama kuin päälävistäjän alkioiden (summan) merkki. Siispä yhtälö on muotoa

> lambda[1]*y[1]^2+lambda[2]*y[2]^2=16;

missä ja ovat positiivisia, joten ellipsihän siitä tulee.

b)

> g:=q-16; # rajoitefunktio

> f:=x^2+y^2; # kohdefunktio

> L:=f+lambda*g; # Lagrangen funktio

> lagyht:={diff(L,x)=0,diff(L,y)=0,g=0};

> solve(lagyht,{x,y,lambda});

> ratk:=map(allvalues,[%]);

> p1:=subs(ratk[1],[x,y]);p2:=subs(ratk[2],[x,y]);p3:=subs(ratk[3],[x,y]);p4:=subs(ratk[4],[x,y]);

> ell:=implicitplot(g=0,x=-3..3,y=-3..3,scaling=constrained,color=blue):

> akseli:=p->line([0,0],p);

> display(ell,akseli(p1),akseli(p2),akseli(p3),akseli(p4));

> sqrt(subs(ratk[1],f));sqrt(subs(ratk[3],f));

Tässä näkyvät pikku- ja isoaksleien puolikkaiden pituudet.

Tarkistus:

> Eigenvectors(A);

> 4*y1^2+2*y2^2=16;

> lhs(%)/16=1;

> iso:=sqrt(8); pieni:=2;

3.

> restart: with(linalg):

Warning, the name changecoords has been redefined

Warning, the protected names norm and trace have been redefined and unprotected

> f:=(x,y,z)->(x/4)^2+(y/4)^2+(z/4)^2;

> g:=x+y+z-L;

> Lag:=f(x,y,z)+lambda*g;

> gr:=grad(Lag,[x,y,z,lambda]);

> solve({gr[1]=0,gr[2]=0,gr[3]=0,g=0},{x,y,z,lambda});

Siis kaikki pätkät yhtä suuria : x=y=z=L/3.

> f(L/3,L/3,L/3); # Pinta-alojen summa:

Reunat: Tällöin jokin muuttuja = 0. Kaksi keskenään erilaista mahdollisuutta (symmetriasyistä):

1) yksi muuttuja = 0 ja 2) kaksi muutujaa = 0

ensin yksi, olkoon z:

> f(x,y,0);

> g:=x+y+0-L;

> Lag:=f(x,y,0)+lambda*g;

> gr:=grad(Lag,[x,y,lambda]);

> solve({gr[1]=0,gr[2]=0,gr[3]=0},{x,y,lambda});

> f(L/2,L/2,0);

Yksi pätkä (ei leikkausta):

> f(L,0,0);

Tässä on kaikki mahdolliisuudet. maksimi on tämä, jossa ei leikata ollenkaan, minimi se, jossa leikataan kolmeen samanpituiseen osaan.

• Huom! Yllä esiintyi kahta tapaa:
• 1) Lagrangen funktion gradientti, eli derivaatta kaikkien muuttujen suhteen ( mukaanlukien) on = 0
• 2) Derivaatta (x:n y:n (ja z:n) suhteen = 0 ja g=0
• Tämä on sama asia, koska derivaatta :n suhteen on juuri g .

4.

> restart:with(plots):with(linalg):with(LinearAlgebra):V2L:=vek->convert(vek,list):

>

Warning, the name changecoords has been redefined

Warning, the protected names norm and trace have been redefined and unprotected

Warning, the assigned name GramSchmidt now has a global binding

Aloitetaan määrittelemällä kohdefunktio f ja gradienttifunktio g. Koska muuttujia on mukava välillä käsitellä jonona tai listana ja välillä taas vektorina, päädyin ehdottamaan kahta märitelmää: f ja fv, jossa jälkimmäisen argumenttina on vektori.

Vastaavasti tehdään g:n ja gv:n tapauksessa.

Kun nämä pikku kömpelyydet kestetään, niin loppu onkin sitten jo mukavaa.

> f:=(x,y)->2*(x^2+y^2)+x*y-5*(x+y);

> fv:=X->2*(X[1]^2+X[2]^2)+X[1]*X[2]-5*(X[1]+X[2]);

> g:=[D[1](f),D[2](f)];

> gv:=v->g(v[1],v[2]);

Tehdään indeksoitu muttuja, johon kerätään SD:n tuottamia vektoreita. Ensin alkupiste:

> x[0]:=<1,-2>;

> N:=5:for i to N do u:=-Normalize(Vector(gv(x[i-1])));
phi:=t->simplify(fv(evalm(x[i-1]+t*u)));
tmin:=solve(diff(phi(t)=0,t));
x[i]:=(evalm(x[i-1]+tmin*u));
od:

> X:=(Matrix(map(V2L,[seq(x[ii],ii=0..5)])));reitti:=convert(X,listlist);
plot(reitti,color=blue,scaling=constrained);
contourplot(f(x,y),x=-1..2,y=-1..3);
display(%,%%);

>

5.

> restart:with(plots):with(linalg):with(LinearAlgebra):V2L:=vek->convert(vek,list):
f:=(x,y)->exp(x)*(4*x^2+2*y^2+4*x*y+2*y+1);
fv:=X->exp(X[1])*(4*X[1]^2+2*X[2]^2+4*X[1]*X[2]+2*X[2]+1);

Warning, the name changecoords has been redefined

Warning, the protected names norm and trace have been redefined and unprotected

Warning, the assigned name GramSchmidt now has a global binding

> g:=[D[1](f),D[2](f)];gv:=v->g(v[1],v[2]);

Aluksi vilkaisu:

> plot3d(f(x,y),x=-1..1,y=-1..1);

> contourplot(f(x,y),x=-2..1,y=-2..0);

>

Minimi näyttäisi olevan jossain ellipsimäisen käyrän sisällä. Kokeillaan alkupisteenä O:a.

> x[0]:=<0,0>;

> u:=-Normalize(Vector(gv(x[0])));

> z:=evalm(x[0]+t*u);

> phi:=t->simplify(fv(evalm(x[0]+t*u)));

> phi(t);

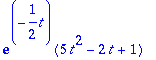
> solve(diff(phi(t)=0,t));

> tmin:=evalf(min(%));

> X[1]:=evalf(x[0]+tmin*u);

>

>

> grad(f(x,y),[x,y]);

> solve({%[1]=0,%[2]=0},{x,y});

solve löytää KRP:t kunnioitettavan hyvin.

> plot3d(f(x,y),x=0..1,y=-2..0,style=patchcontour);

> contourplot(f(x,y),x=0..1,y=-2..0,contours=20);

Tämä ei ole ihan helppo tapaus. Viivahaun minimin määrittäminen ei sujukaan ihan mekaanisesti.

Tässä täytyisi edetä askel kerrallaan tai sitten implementoida interpolaatioon perustuva algoritmi.

No, jätetään tähän, kokeissahan ei sellaiset komplikaatiot tule kysymykseen.

6.

Kertauksen vuoksi jyrkimmän laskun menetelmän proseduuri:
Olkoon f(x) funktio, jonka minimiä haemme. valitaan alkupiste x(0).
1. minimoidaan f suoralla : x[n]-t*grad(f(x[n])) (t > 0)
2. päivitetään: x[n+1]:=x[n] + tmin*u, missä u = -grad(f(x[n])).

> restart:f:=(x,y)->x^2+c*y^2;
fv:=X->X[1]^2+c*X[2]^2;
g:=[D[1](f),D[2](f)];
gv:=v->g(v[1],v[2]);
#gv(x[0]); g(1,-2);
X0:=evalm(a*<c,1>);
evalm(-gv(X0));
u:=evalm(-gv(X0)/(2*a*c));
phi:=t->simplify(fv(evalm(X0+t*u)));
phi(t);
(c-t)^2+c*(1-t)^2: expand(%): collect(%,t^2);
collect(phi(t),t^2);
tmin:=solve(diff(phi(t),t)=0,t);
X1:=map(normal,evalm(X0+tmin*u));

Warning, the name changecoords has been redefined

> c:=20.:seq(c*(c-1)^n/(c+1)^n,n=10..20);
seq(c*(c-1)^n/(c+1)^n,n=21..40);
seq(c*(c-1)^n/(c+1)^n,n=100..110);
c:=40.:
seq(c*(c-1)^n/(c+1)^n,n=200..201);

>

Suppenee hitaaasti, mutta nyt en jaksa selostaa enempää.