![gaussmn := Sum(Sum(wx[i]*wy[j]*intf(sx[i],sy[j]),j ...](images/harj12lv1.gif)
Harj. 12 LV
25.4.02 HA
Alustukset
> restart:
Warning, the name changecoords has been redefined
> #read("c:\\opetus\\maple\\v202.mpl"): # HA:n kotikone (Win)
> #read("/p/edu/mat-1.414/maple/v202.mpl"): # ATK-luokassa
> read("/home/apiola/opetus/peruskurssi/v2-3/maple/v202.mpl"): # HA:n Linux
> with(plots):
Huom! Ennenkuin suoritat komentoja, poista read-lauseista soveltuvasti kommentit ja tarpeen mukaan muuta polkua.
1.
Kun käytettävissä on harj12av.mws, niin opettvaisinta lienee laskea ensin aivan samalla tavalla ottamalla vain
isommat gausstaulukot käyttöön.
> restart:
Warning, the name changecoords has been redefined
>
read("/home/apiola/opetus/peruskurssi/v2-3/maple/v202.mpl"):
#read("/p/edu/mat-1.414/maple/v202.mpl")
#read("c:\\opetus\\maple\\v202.mpl"):
> gaussmn:=Sum(Sum(wx[i]*wy[j]*intf(sx[i],sy[j]),j=1..n),i=1..m);
![gaussmn := Sum(Sum(wx[i]*wy[j]*intf(sx[i],sy[j]),j ...](images/harj12lv1.gif)
Tässä on yleinen tulokaava. Lasketaan nyt AV teht. 5:n tilanne
> m:=5: sx:=gaussolmut(m);wx:=gausspainot(m);
![]()
![]()
> n:=4: sy:=gaussolmut(n):wy:=gausspainot(n):
Tässä on yleinen tulokaava. Lasketaan nyt AV teht. 5:n tilanne.
> f:=(x,y)->ln(x+2*y);
![]()
> x:=0.3*u+1.7; y:=0.25*v+1.25;
![]()
![]()
> dxdy_per_dudv:=.3*.25;
![]()
> F:=f(x,y);
![]()
Muunsimme integroinnin yksikköneliön yli (kuten AV 5:ssä).
> intf:=unapply(F*dxdy_per_dudv,u,v);
![]()
> value(gaussmn);
![]()
> int(int(f(xx,yy),xx=1.4..2),yy=1..1.5);
![]()
> f_arvoja=m*n;
![]()
Saatiin 9 oikeaa numeroa.
Siinä voi testailla lisää ...
Kokeillaan samalla valmiita funktioitamme
> gtaulux:=gausstaulukko(5): gtauluy:=gausstaulukko(4):
> Gaussnelio(gtaulux,gtauluy,intf);
![]()
> Gaussnelio(gtauluy,gtaulux,intf);
![]()
> Gaussnelio(gtauluy,gtauluy,intf);
![]()
> Gaussnelio(gtaulux,gtaulux,intf);
![]()
> Gaussnelio(gausstaulukko(3),gausstaulukko(3),intf);
![]()
> with(LinearAlgebra):
> Matrix(3,3,(m,n)->Gaussnelio(gausstaulukko(m),gausstaulukko(n),intf));
![_rtable[136799956]](images/harj12lv18.gif)
> Matrix(5,5,(m,n)->Gaussnelio(gausstaulukko(m),gausstaulukko(n),intf));
![_rtable[135883796]](images/harj12lv19.gif)
Tämä on tosi eleganttia, kylläkin tuhlailevaa laskentaa. Lähes sama eleganssi voitaisiin saavuttaa laskemalla ensin valmiit taulukot ja sitten hakemalla niistä. Jos tehtäisiin isompi taulukko, niin sitten kannattaisi jossain vaiheessa.
Gaussin kaavoja käytetään elävässä elämässä tietysti niin, että muodostetaan ensin sopivan kokoinen taulukko ja sitten
haetaan aina sieltä. Siksi funktiomme onkin rakennettu niin, että taulukko annetaan argumenttina. (Taulukko voitaisiin vaikka
lukea tiedostosta.)
Gaussxy :n kokeilu:
Tämä on sikäli helppokäyttöisempi, että ei tarvita muuttujan vaihtoa:
> map(nops,gtaulux); map(nops,gtauluy);
![]()
![]()
> op(f);
![]()
> Gaussxy(gtaulux,gtauluy,f,1.4,2,1,1.5);
![]()
> Gaussnelio(gtaulux,gtauluy,intf);
![]()
Kylläpä toimivat kauniisti!
2.
> restart:with(plots): with(plottools):
Warning, the name changecoords has been redefined
Warning, the name arrow has been redefined
>
kolmio:=[[0,0],[1,0],[1,1]]:kolmiokuva:=polygon(kolmio,filled=true,color=yellow):
> display(kolmiokuva);"xy-taso";
![[Maple Plot]](images/harj12lv25.gif)
![]()
>
nelio01:=[[0,0],[0,1],[1,1],[1,0]]:
>
nelio01kuva:=polygon(nelio01,filled=true,color=green):
> display(nelio01kuva);"uv-taso";
![[Maple Plot]](images/harj12lv27.gif)
![]()
>
nelio_11:=[[1,1],[-1,1],[-1,-1],[1,-1]]:
>
nelio_11kuva:=polygon(nelio_11,filled=true,color=cyan):
>
display(nelio_11kuva); "zw-taso";
![[Maple Plot]](images/harj12lv29.gif)
![]()
Olkoot:
> g:=(u,v)->[u,u*v]; gv:=uv->g(uv[1],uv[2]); # Kuvaus [0,1] x [0,1] --> Delta (kolmio)
![]()
![]()
> h:=(w,z)->[(w+1)/2,(z+1)/2]; hv:=uv->h(uv[1],uv[2]); # Kuvaus [-1,1] x [-1,1] --> [0,1] x [0,1] .
![]()
![]()
Aivan samoin kuin optimoinnin yhteydessä (Muistatko SD:n?) on kätevää määritellä kahden muuttujan funktioista myös lista/vektori-versiot
gv
ja
hv
.
Niiden avulla on vaivatonta katsoa, miten eri pisteet kuvautuvat.
> map(hv,nelio_11);map(gv,%);
![]()
![]()
Näinhän niiden pitikin mennä.
Katsotaan Gaussin pisteitä. Voi olla, että olemme käyttäneet restarttia, no tiedämme, mitä pitää olla:
> s[1]:=-1/sqrt(3); s[2]:=-s[1];
![]()
![]()
> ss:=[seq(seq([s[i],s[j]],j=1..2),i=1..2)];
![]()
> gpnelio01:=map(hv,ss);
![]()
>
display(nelio01kuva,plot(gpnelio01,style=point,symbol=cross)); "uv-taso";
![[Maple Plot]](images/harj12lv41.gif)
![]()
> gpkolmio:=map(gv@hv,ss); # Näin kuvautuvat neliön [-1,1] x [-1,1] Gauss2-pisteet kolmioon Delta.
![]()
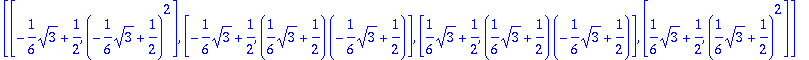
> display(kolmiokuva,plot(gpkolmio,style=point,symbol=cross));
![[Maple Plot]](images/harj12lv45.gif)
Gaussin pisteiden sijainti kolmiossa ei näytä optimaaliselta. Oikeassa laidassa pisteet ovat paljon harvemmassa.
Miettimisen paikka: Mitä kannattaisi tehdä. Jaetaan alue sopivasti osiin. Ehkä kannattaisi ottaa suht. iso N vaakasuunnassa ja kutakin
pystyjanaa kohti kasvatettaisiin N:ää lineaarisesti pystysuunnassa. Näillä Gauss-palikoilla olisi helppo toteuttaa.
Parempi vielä: Siirrytään käyttämään ns. pinta-alakoordinaatteja: Kolmion sisäpiste yhdistetään janalla kuhunkin kärkeen ja otetaan syntyneiden kolmioiden
pinta-alat pisteen koordinaateiksi.
FEM-laskennassa suoritetaan usein integrointia kolmion yli, Pisteet valitaan usein reunalta, mediaanien leikkauspisteestä jne., riippuen kantafunktiotyypistä.
Periaatteessa tehdään samanlainen mahd. korkean asteluvun vaatimus.
Tutkimuksen ja opiskelun aihe ... FEM-kirjallisuus ... (FEM = Finite Element Method)
Testataan integraalikaavoja esimerkeillä.
>
f:='f':Ixy:=Int(Int(f(x,y),y=0..x),x=0..1);
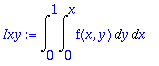
>
Iuv:=Int(Int(f(u,u*v)*u,v=0..1),u=0..1);
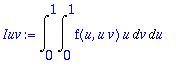
>
Iwz:=(1/8)*Int(Int(f((w+1)/2,(w+1)/2*(z+1)/2)*(w+1),z=-1..1),w=-1..1);
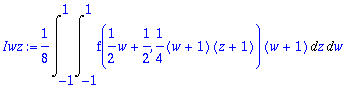
> f:=(x,y)->x*y; fv:=xvek->f(xvek[1],xvek[2]);
![]()
![]()
>
value(Ixy);
![]()
>
value(Iuv);
![]()
>
value(Iwz);
![]()
Näyttää menneen oikein.
Tehdään nyt tehtävn AV 6 esimerkki.
> f:=(x,y)->exp(-x^2*y^2); fv:=xvek->f(xvek[1],xvek[2]);
![]()
![]()
> uv:=h(w,z); xy:=gv(uv);
![]()
![]()
> intfunwz:=1/8*(w+1)*fv(xy);
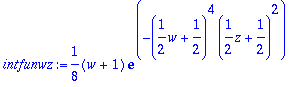
> Int(Int(intfunwz,z=-1..1),w=-1..1): %=value(%);evalf(rhs(%));
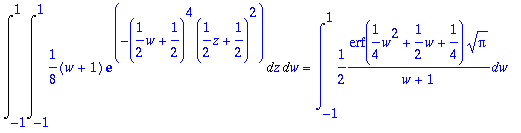
![]()
> x:='x': y:='y':Int(Int(f(x,y),y=0..x),x=0..1): %=value(%); evalf(rhs(%));
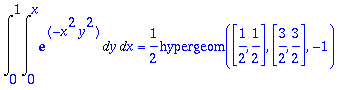
![]()
Saatiinpa samalla näyttö Maplen taidoista laskea erikoisfunktioilla (erf ja hypergeom).
Ja sama tuli.
No nyt sitten Gaussiin.
>
#read("/home/apiola/opetus/peruskurssi/v2-3/maple/v202.mpl"):
#read("/p/edu/mat-1.414/maple/v202.mpl")
> gtaulux:=gausstaulukko(5);
![]()
> gtauluy:=gausstaulukko(4);
![]()
> fzw:=unapply(intfunwz,w,z);
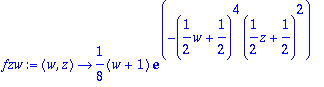
> op(Gaussnelio);
![]()
> Gaussnelio(gtaulux,gtauluy,fzw);
![]()
Olipa tarkka. Otetaan vähemmän pisteitä
> gtaulu2:=gausstaulukko(2):gtaulu3:=gausstaulukko(3):gtaulu4:=gausstaulukko(4):
> Gaussnelio(gtaulu2,gtaulu3,fzw);
![]()
> Gaussnelio(gtaulu3,gtaulu2,fzw);
![]()
3.
Lieriökoordinaatteihin siirtyminen auttaa merkittävästi laskennassa, kuten numint3.mws :ssä näemme.
Lasketaan kartion z=r massa ja momentti xy-tason suhteen, kun kartion tiheys
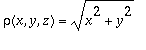 .
.
Edellinen saadaan copy/paste:lla:
>
restart: read("/home/apiola/opetus/peruskurssi/v2-3/maple/v202.mpl"):#
#read("/p/edu/mat-1.414/maple/v202.mpl")
#read("c:\\opetus\\maple\\v202.mpl"):
Warning, the name changecoords has been redefined
> M:=Int(Int(Int(r*r,z=r..2),r=0..2),Theta=0..2*Pi);
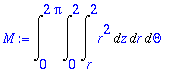
> Mxy:=Int(Int(Int(z*r*r,z=r..2),r=0..2),Theta=0..2*Pi);
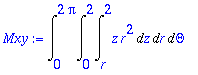
(Integraaleissa r on tiheysfunktio, toinen r on Jakobin det.)
> gtaulu:=gausstaulukko(5):
> Mg:=Gaussxyz(gtaulu,gtaulu,gtaulu,(Theta,r,z)->r^2,0,2*Pi,0,2,(Theta,r)->r,2);
![]()
> value(M);evalf(%);
![]()
![]()
> Mgxy:=Gaussxyz(gtaulu,gtaulu,gtaulu,(Theta,r,z)->z*r^2,0,2*Pi,0,2,(Theta,r)->r,2);
![]()
> value(Mxy);evalf(%);
![]()
![]()
> z0g:=Mgxy/Mg;
![]()
> z0:=value(Mxy)/value(M);evalf(%);
![]()
![]()
Saatiinpa tarkkaan, ja vain 125 funktion arvoa avaruudessa! Voitaisiin laskea x0 ja y0, mutta pakkohan niistä on symmetriasyistä tulla 0. Jätetään siksi tähän.
4.
> restart:with(linalg):
Warning, the name changecoords has been redefined
Warning, the protected names norm and trace have been redefined and unprotected
Torus:
>
x:=(a+w*cos(v))*cos(u);
y:=(a+w*cos(v))*sin(u);
z:=w*sin(v);
![]()
![]()
![]()
> Jac:=jacobian([x,y,z],[u,v,w]);
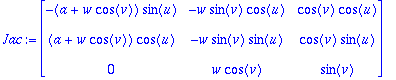
> Jdet:=simplify(det(%));
![]()
> M2:=Int(Int(Int(Jdet,w=0..b),v=0..2*Pi),u=0..2*Pi);
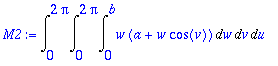
> M:=value(%)/2;
![]()
Keskiön suhteen kiinnostava on x0. Symmetriasyistä on oltava y0=0, z0=0.
> x;
![]()
> Mxy:=Int(Int(Int(x*Jdet,w=0..b),v=0..2*Pi),u=-Pi/2..Pi/2);
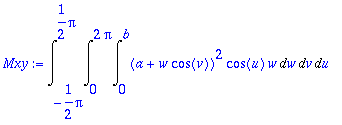
> value(Mxy);
![]()
> x0:=%/M;
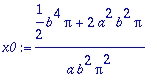
> x0:=simplify(%);
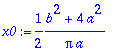
> subs(a=2,b=1,x0);evalf(%);
![]()
![]()
5.
> restart:with(plots): with(plottools):
Warning, the name changecoords has been redefined
Warning, the name arrow has been redefined
>
read("/home/apiola/opetus/peruskurssi/v2-3/maple/v202.mpl"):
#read("/p/edu/mat-1.414/maple/v202.mpl")
> T:=[[-1,1],[-1,1]];
![]()
> satu:=rand(0..10^10)/10.^10;
![]()
![]()
![]()
![]()
![]()
> N:=100: [MonteCarlo2d(1,(x,y)->x^2+y^2,T,N^2),Riemann2d(1,(x,y)->x^2+y^2,T,N)]; N^2*f_arvoa;
![]()
![]()
> N:=20: lkm:=20: keskiarvo:=add(MonteCarlo2d(1,(x,y)->x^2+y^2,T,N^2),i=1..lkm)/lkm;lkm*N^2*f_arvoa;
![]()
![]()
> N:=30: lkm:=10: keskiarvo:=add(MonteCarlo2d(1,(x,y)->x^2+y^2,T,N^2),i=1..lkm)/lkm;lkm*N^2*f_arvoa;
![]()
![]()
Monte-Carlo näyttää olevan joka kerta parempi kuin Riemann. Ero näkyy erityisen selvästi pienillä laskentamäärillä. "Hyvällä onnella" saadaan Monte Carlolla varsin kohtuullinen
likiarvo hyvinkin pienellä laskentamäärällä. Toissaalta Monte Carlo saattaa isollakin laskennalla antaa yllättävästi huonomman tulloksen kuin pienemmällä.
Kannattaako siis uhkapeli?
6.
> restart:
Warning, the name changecoords has been redefined
> with(plots): setoptions3d(axes=boxed,orientation=[-30,50]):
>
read("/home/apiola/opetus/peruskurssi/v2-3/maple/v202.mpl"):
#read("/p/edu/mat-1.414/maple/v202.mpl")
Toruspinta:
>
x:=(a+b*cos(v))*cos(u);
y:=(a+b*cos(v))*sin(u);
z:=b*sin(v);
![]()
![]()
![]()
Toki on luonnollista laskea toruskoordinaateissa, kuten teht. 4. Tyypillinen Monte Carlo olisi sellainen, jossa reunat olisivat hankalammat, kuten luentoesimerkissä.
Tällöin olisi luontevaa laskea suorak. koordinaateissa. (Samaten tehtävässä, joka olisi suoraan annettu suorak. koord.) Sitäpaitsi särmiön yli integroinnissa ei ole
kovin paljon vitsiä Monte Carlon suhteen.
Muunnetaan suorakulmaisiin koordinaatteihin.
Tämä tapahtuu etupäässä käsin. Käytämme Maplea tässä kohden lähinnä matemaattiseen tekstinkäsittelyyn, toki hyödynnämme
hänen sievennystaitojaan.
> x2y2z2:=simplify(x^2+y^2)+z^2;
![]()
> x:='x': y:='y': z:='z':
> x2y2z2:=a^2+2*a*(sqrt(x^2+y^2)-a)+b^2*cos(v)^2+b^2*sin(v)^2;
>
![]()
> expand(x2y2z2);
![]()
> x^2+y^2+z^2+a^2=expand(2*a*(sqrt(x^2+y^2)-a))+b^2;
![]()
> x^2+y^2+z^2+a^2-2*a*(sqrt(x^2+y^2))=b^2;
![]()
Kun ajatellaan
> r=sqrt(x^2+y^2);
![]()
nähdään vasemmalla binomin neliö. Siten saadaan:
> (sqrt(x^2+y^2)-a)^2+z^2=b^2;
![]()
Toruksen sisusta on siten:
> (sqrt(x^2+y^2)-a)^2+z^2<=b^2;
![]()
Kannattaa laskea kynällä ja paperilla.
>
x:=(a+b*cos(v))*cos(u);
y:=(a+b*cos(v))*sin(u);
z:=b*sin(v);
![]()
![]()
![]()
> a:=2: b:=1:
> plot3d([x,y,z],u=-Pi/2..Pi/2,v=0..2*Pi,scaling=constrained,labels=["x","y","z"]);
![[Maple Plot]](images/harj12lv122.gif)
Kuvassa on suoraan ympäröivä laatikko
> T:=[[0,3],[-3,3],[-1,1]];
![]()
> satu:=rand(0..10^9)/10.^9;
![]()
![]()
![]()
![]()
![]()
> g:=(x,y,z)->(sqrt(x^2+y^2)-a)^2+z^2;
![]()
> MonteCarlo3d(1,g,T,10),evalf(a*b^2*Pi^2);
![]()
> MonteCarlo3d(1,g,T,20),evalf(a*b^2*Pi^2);
![]()
>