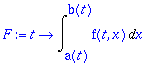
Harj. 12 AV
20.4.02 HA
1.
> restart:
Warning, the name changecoords has been redefined
> F:=t->Int(f(t,x),x=a(t)..b(t));
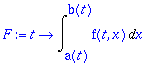
> dF:=diff(F(t),t);
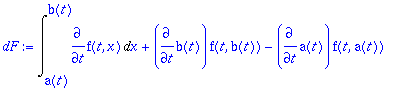
Maple osaa kyllä soveltaa ketjusääntöä ja muita yleisiä lauseita.
Määritellään nyt f tehtävän funktioksi.
> f:=(t,x)->sin(x/t)/x;
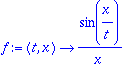
> a:=t->t: b:=t->t^2;
![]()
> F(t);
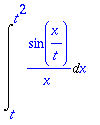
> diff(F(t),t);
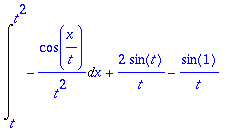
> simplify(value(%));
![]()
Kannattaa laskea pitemmälle käsin. Tässä on helppo tehdä laskuvirheitä, jos tarkkaavaisuus hetkeksi herpaantuu.
Seuraava ei kuulu enää osattaviin asioihin, mutta kun Maple helposti tarjoilee Si-funktiota, niin katsotaan:
Maple siis tuntee erikoisfunktion Si:
> Int(sin(x)/x, x=0..t): value(%)=%; # Tässä tapauksessa saadaan looginen järjestys näinpäin.
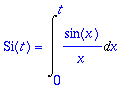
> F(t)=value(F(t));
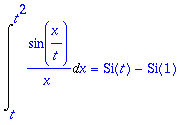
> Diff(lhs(%),t)=diff(rhs(%),t);
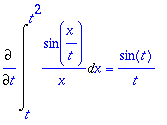
Maple osasi palauttaa kysytyn tehtävän suoraan Si-funktion derivaataksi, joka tietysti on yllä oleva sin(t)/t .
2.
> f:=1/(x+y);
![]()
> c:=15: plot(1/x,x=1..c,color=yellow,filled=true);
![[Maple Plot]](images/harj12av12.gif)
> c:='c':II:=Int(Int(f,y=0..1/x),x=1..c);
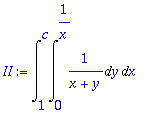
> II:=Int(int(f,y=0..1/x),x=1..c);
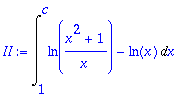
> II:=int(int(f,y=0..1/x),x=1..c);

> Int(ln(1+1/x^2),x): %=value(%);
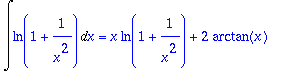
> int(ln(1+1/x^2),x=1..c);

> limit(%,c=infinity);
![]()
Raja-arvo on olemassa, joten integraali suppenee, ja sen arvo on tässä. Tätä nyt ei ihan voitane pitää todistuksena.
Käsin laskien nähdään, että arctan(c) ->
![]()
Siis tarvitsemme raja-arvon (c ->
![]() ) lausekkeelle
) lausekkeelle
> c*ln(1+1/(c^2));
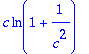
Helpointa on ottaa pari termiä Taylorin kehitelmästä:
> c*subs(x=1/c^2,taylor(ln(1+x),x=0,2));expand(%);
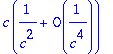
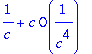
Tämä siis lähenee 0:aa, kun c->
![]() , joten saamme tosiaankin yllä olevan tuloksen.
, joten saamme tosiaankin yllä olevan tuloksen.
3.
> with(plots): with(plottools):
> f:=1/(x*y);
![]()
> c:=.1: display(plot([x^2,x],x=0..1),line([c,c^2],[c,c]));
![[Maple Plot]](images/harj12av26.gif)
Tässä rajataan paha piste O pois ottamalla c>0, ja lasketaan ao. integraalien raja-arvo, kun c ->
![]() .
.
> c:='c':Int(1/x*int(1/y,y=x^2..x),x=c..1);
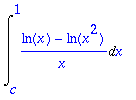
> value(%);simplify(%,symbolic);
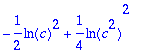
![]()
Luonnollisempaa on käsin laskettaess sieventää integroitavan logaritmit:
> 1/x*int(1/y,y=x^2..x);simplify(%,symbolic);int(%,x=c..1);
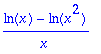
![]()
![]()
Raja-arvo on ,
![]() joten integraali hajaantuu.
joten integraali hajaantuu.
4.
> restart:
Warning, the name changecoords has been redefined
Määrättävä solmut x1,x2 ja painot w1,w2 siten, että integrointikaava
> Int(f(x),x=-1..1)=w[1]*f(x[1])+w[2]*f(x[2]);
![Int(f(x),x = -1 .. 1) = w[1]*f(x[1])+w[2]*f(x[2])](images/harj12av35.gif)
on tarkka kaikille astetta 3 oleville polynomeille. Välttämätöntä ja riittävää: tarkka kaikille monomeille
> 1,x,x^2,x^3;
![]()
> Gauss2yht:={seq(Int(x^k,x=-1..1)=w1*x1^k+w2*x2^k,k=0..3)};
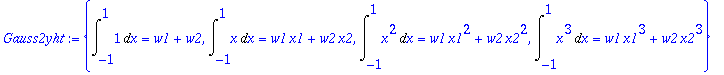
Muutetaan Int -> int, jolloin integraalit lasketaan:
> gauss2yht:={seq(int(x^k,x=-1..1)=w1*x1^k+w2*x2^k,k=0..3)};
![]()
> solve(gauss2yht,{x1,x2,w1,w2});map(allvalues,%);
![]()
![]()
> assign(%);
> x1;x2;
![]()
![]()
> s[1]:=min(x1,x2); s[2]:=max(x1,x2); w[1]:=w1; w[2]:=w2;
![]()
![]()
![]()
![]()
Pantiin talteen seuraavaa tehtävää varten. (Muista: älä tee restarttia ennen tehtävää 5.)
5.
> with(plots): with(plottools):
Kun suoritat tehtävän 4, niin Gaussin 2. asteen säännön solmut ovat muuttujissa s[1] ja s[2] ja painot muuttujissa
w[1] ja w[2]. Tarkistetaan:
> s[1],s[2],w[1],w[2];
![]()
> Sum(Sum(w[i]*w[j]*f(s[i],s[j]),j=1..2),i=1..2);
![Sum(Sum(w[i]*w[j]*f(s[i],s[j]),j = 1 .. 2),i = 1 .....](images/harj12av48.gif)
> gauss2:=value(%);
![]()
> f:=(x,y)->ln(x+2*y);
![]()
> x:=0.3*u+1.7; y:=0.25*v+1.25;
![]()
![]()
> dxdy_per_dudv:=.3*.25;
![]()
> F:=unapply(f(x,y),u,v);
![]()
> Sum(Sum(w[i]*w[j]*F(s[i],s[j])*dxdy_per_dudv,j=1..2),i=1..2);
![Sum(Sum(.75e-1*w[i]*w[j]*ln(.3*s[i]+4.20+.50*s[j]),...](images/harj12av55.gif)
> value(%);
![]()
> x:='x': y:='y':
> int(int(f(x,y),x=1.4..2),y=1..1.5);
![]()
>
Hämmästyttävää, laskettiin funktion arvo 4:ssä pisteessä ja saatiin 4 oikeaa numeroa integraaliin!
6. Säästetään LV:oon