Harj. 11 LV
19.4.02 HA ja JP
Alustukset
>
restart:
with(plots):with(plottools): with(linalg):
setoptions3d(axes=boxed,orientation=[-30,50]):
Warning, the name changecoords has been redefined
Warning, the protected names norm and trace have been redefined and unprotected
1.
>
restart:
with(plots):with(plottools):with(linalg):
setoptions3d(axes=boxed,orientation=[-30,50],scaling=constrained):
Warning, the name changecoords has been redefined
Warning, the protected names norm and trace have been redefined and unprotected
Torus
>
x:=cos(u)*(a+b*cos(v));
y:=sin(u)*(a+b*cos(v));
z:=b*sin(v);a:=2:b:=1/2:
u:=0: plot([x,z,v=0..2*Pi],-(a+b)..a+b,scaling=constrained);
![]()
![]()
![]()
![[Maple Plot]](images/harj11lv4.gif)
Tämä ympyrä, kun pyörähtää z-akselin ympäri, syntyy torus:
> u:='u':x;
![]()
>
u:='u':plot3d([x,y,z],u=0..2*Pi,v=0..2*Pi);
![[Maple Plot]](images/harj11lv6.gif)
Katsotaan toruksen sisään jättämällä parametrialueet vajaiksi.
>
plot3d([x,y,z],u=0..4*Pi/3,v=-Pi/2..Pi-0.2,axes=none);
![[Maple Plot]](images/harj11lv7.gif)
Kokeillaan "kiellettyä" tubeplottia.
> tubeplot([cos(t),sin(t),0],t=0..2*Pi,radius=0.3);
![[Maple Plot]](images/harj11lv8.gif)
> a:='a':b:='b':u:='u':v:='v':
> R:=[x,y,z];
![]()
> Ru:=map(diff,R,u);Rv:=map(diff,R,v);
![]()
![]()
> n:=crossprod(Ru,Rv);
![]()
> normi2:=n[1]^2+n[2]^2+n[3]^2:normi2:=simplify(%);
![]()
> normi:=sqrt(normi2); normi:=simplify(%,symbolic);
![]()
![]()
> ala:=int(int(normi,u=0..2*Pi),v=0..2*Pi);
![]()
>
>
2. (AV 4)
> restart: with(plots): with(linalg):setoptions3d(axes=boxed,orientation=[-30,50]):
Warning, the name changecoords has been redefined
Warning, the protected names norm and trace have been redefined and unprotected
> S:=[3*cos(u),3*sin(u),v];
![]()
> pinta:=plot3d(S,u=0..Pi/2,v=0..2,labels=["x","y","z"]):
>
> F:=[exp(2*y),exp(-2*z),exp(2*x)];
![]()
> kentta:=fieldplot3d(F,x=0..3,y=0..3,z=0..2):
> display(kentta,pinta);
![[Maple Plot]](images/harj11lv19.gif)
> r:=S;
![]()
> ru:=map(diff,r,u);
![]()
> rv:=map(diff,r,v);
![]()
> N:=crossprod(ru,rv);
![]()
> intf:=innerprod(subs(x=3*cos(u),y=3*sin(u),z=v,F),N);
![]()
> Int(Int(intf,u=0..Pi/2),v=0..2);
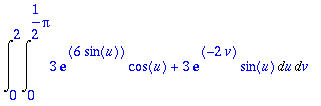
> tulos:=value(%);
![]()
> evalf(tulos),evalf(2*sinh(6));
![]()
Ei siitä aivan samaa tule kuin vastauksessa. Tehtävä ja vastaus ovat KRE-kirjasta. Yllä oleva lasku on kyllä oikein, en usko mitenkään, että Maplekaan tällaisissa
rutiinilaskuissa voisi möhliä.
Maagista kylläkin, likiarvot ovat 3:lla numerolla samat, mutta ei tämä silti mikään pyöristysvirhe ole!
3. LV pinta [u*cos(v),u*sin(u),3*v]
> restart: with(plots): with(linalg):setoptions3d(axes=boxed,orientation=[-30,50]):
Warning, the name changecoords has been redefined
Warning, the protected names norm and trace have been redefined and unprotected
> F:=[x^2,y^2,z^2];
![]()
> r:=[u*cos(v),u*sin(u),3*v];
![]()
> pinta:=plot3d(r,u=0..1,v=0..2*Pi):
> kentta:=fieldplot3d(F,x=-1..1,y=-1..1,z=0..3*2*Pi):
> display(pinta,kentta);
![[Maple Plot]](images/harj11lv30.gif)
> ru:=map(diff,r,u);
![]()
> rv:=map(diff,r,v);
![]()
> N:=crossprod(ru,rv);
![]()
> intf:=innerprod(subs(x=u*cos(v),y=u*sin(u),z=3*v,F),N);intf:=simplify(%);
![]()
![]()
> Int(Int(intf,u=0..1),v=0..2*Pi);
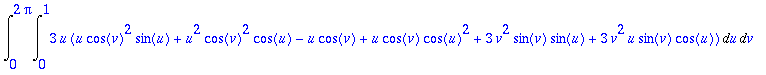
> tulos:=value(%);
![]()
Mikäpä siinä, pintahan se on tuollainenkin.
Tarkoitukseni oli kuitenkin laittaa ruuvipinta, eli kierreporras (Helicon). Lasketaan nyt sekin:
>
3 LV pinta [u*cos(v),u*sin(v),3*v] eli ruuvipinta
>
restart: with(plots): with(linalg):setoptions3d(axes=boxed,orientation=[-30,50]):
Warning, the name changecoords has been redefined
Warning, the protected names norm and trace have been redefined and unprotected
> F:=[x^2,y^2,z^2];
![]()
>
r:=[u*cos(v),u*sin(v),3*v];
![]()
>
pinta:=plot3d(r,u=0..1,v=0..2*Pi):
>
kentta:=fieldplot3d(F,x=-1..1,y=-1..1,z=0..3*2*Pi):
>
display(pinta,kentta);
![[Maple Plot]](images/harj11lv40.gif)
>
ru:=map(diff,r,u);
rv:=map(diff,r,v);
![]()
![]()
>
N:=crossprod(ru,rv);
![]()
>
intf:=innerprod(subs(x=u*cos(v),y=u*sin(v),z=3*v,F),N);intf:=simplify(%);
![]()
![]()
>
Int(Int(intf,u=0..1),v=0..2*Pi);
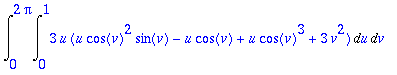
>
tulos:=value(%);
![]()
Saatiin ainakin sievempi tulos.
4 LV
> restart: with(plots): with(linalg):
Warning, the name changecoords has been redefined
Warning, the protected names norm and trace have been redefined and unprotected
> r:=[(2+cos(v))*cos(u),(2+cos(v))*sin(u),sin(v)];
![]()
>
pinta:=plot3d(r,u=0..2*Pi,v=0..Pi,scaling=constrained,axes=frame):
> display(pinta);
![[Maple Plot]](images/harj11lv49.gif)
Tässä on siis toruksen puolikas, kun b=1 ja a=2 (vrt. teht. 1)
>
> Ru:=map(diff,r,u);Rv:=map(diff,r,v);
![]()
![]()
> N:=crossprod(Ru,Rv);
![]()
> normi2:=N[1]^2+N[2]^2+N[3]^2:normi2:=simplify(%);
![]()
> normi2:=sqrt(normi2);
![]()
> Ala:=int(int(normi2,u=0..2*Pi),v=0..Pi); # Teht. 1:ssä laskettiin: Toruksen ala=4Pi^2 ab, puolikkaaksi tulee siis juuri tämä:
![]()
> Int(Int(sin(v)*normi2,v=0..Pi),u=0..2*Pi);
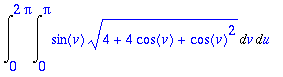
> Mz:=value(%); Mz/Ala=evalf(Mz/Ala);
![]()
![]()
Tässä on z-koordinaatti, joka on se kiinnostava. x0 ja y0 ovat tietysti = 0. Lasketaan nyt nekin:
> Int(Int((2+cos(v))*sin(u)*normi2,v=0..Pi),u=0..2*Pi);
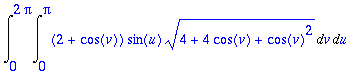
> My:=value(%);
![]()
> Int(Int((2+cos(v))*cos(u)*normi2,v=0..Pi),u=0..2*Pi);Mx:=value(%);
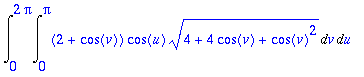
![]()
> keskio:=[Mx/Ala,My/Ala,Mz/Ala];evalf(keskio);
![]()
![]()
5. AV
> restart: with(plots): with(linalg):
Warning, the name changecoords has been redefined
Warning, the protected names norm and trace have been redefined and unprotected
> g:=sqrt(4*a^2-x^2-y^2);
![]()
> muuntosuhde:=sqrt(simplify(1+diff(g,x)^2+diff(g,y)^2));
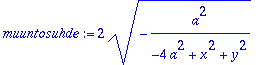
> muuntosuhde:=simplify(%,symbolic);
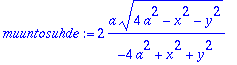
> muuntosuhde:=algsubs(x^2+y^2=r^2,%);
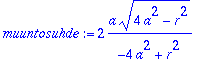
> int(int(r*abs(muuntosuhde),r=0..2*a*sin(Theta)),Theta=0..Pi);

> simplify(%,symbolic);factor(%);
![]()
![]()
Vaihtoehtoisesti pallopinnan palan voisi vaikka näin:
>
x:=v*cos(u):
y:=v*(1+sin(u));
![]()
> z:=sqrt(4*a^2-x^2-y^2);
![]()
> simplify(z^2,symbolic);
![]()
> z:=simplify(sqrt(%),symbolic);
![]()
> r:=[x,y,z];
![]()
> ru:=map(diff,r,u);
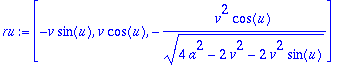
> rv:=map(diff,r,v);
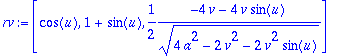
> N:=crossprod(ru,rv);
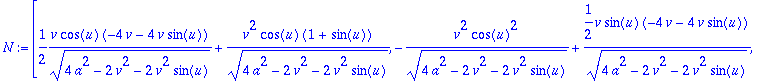
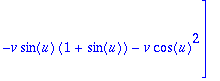
> N:=map(simplify,%);
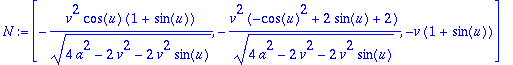
> normi2:=norm(N,2)^2;
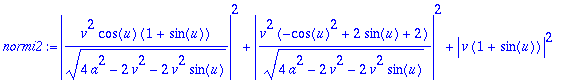
> simplify(%,symbolic);
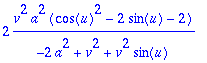
> muunto:=sqrt(%);
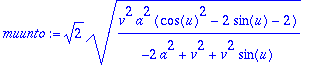
> Int(Int(muunto,u=0..2*Pi),v=0..a);
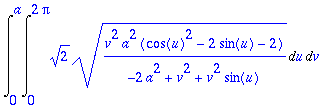
> evalf(%);
Error, (in evalf/int) unable to handle singularity
>
Tätä ei Maple pysty integroimaan, edes numeerisesti. (Voisihan tuohon soveltaa noita Gauss-kapineitamme.)