H/harj10lv
12.4.02 HA
Tässä mukana myös AV
Alustukset
> restart:
Warning, the name changecoords has been redefined
> with(plots):with(plottools):
Warning, the name arrow has been redefined
>
setoptions3d(axes=boxed,orientation=[-30,50]):
Annamme erityisesti erilaisia piirtämisohjeita. Aloitetaan AV-tehtävistä.
Kts. myös int23d.mws .
AV-harjoitukset
AV 1.
> f:=(x,y)->x*y^2+y^3;
![]()
> pinta:=plot3d(f(x,y),x=0..2,y=1..3,view=[0..2,1..3,0..50]):
Käytetään tässä hiukan erilaista tekniikkaa kuin seuraavissa, jotka ovat yleisluonteisempia. Toisaalta on hyvä oppia myös polygonien käyttö, joka on kätevää, kun halutaan piirtää suoria särmiä. Tarvitaan pakkaus plottools .
> pohja:=[[0,1],[2,1],[2,3],[0,3]];pohja3d:=[[0,1,0],[2,1,0],[2,3,0],[0,3,0]];
![]()
![]()
> fv:=x->f(x[1],x[2]): # Taas tämä vektoriversio on kätevä.
> kansiz:=map(fv,pohja); # Funktion arvot pohjanurkissa.
![]()
> kansi3d:=zip((x,y)->[op(x),y],pohja,kansiz); # Eleganttia temppu!
![]()
Rakennetaan sivuseinä kerrallaan, jätetään kaarevareunaiset seinät auki.
> display(polygon(pohja3d),polygon([pohja3d[1],kansi3d[1],kansi3d[2],pohja3d[2]]),polygon([pohja3d[3],kansi3d[3],kansi3d[4],pohja3d[4]]),pinta,style=patchnogrid);
![[Maple Plot]](images/harj10lv6.gif)
2.
> karjet:=[-1,0],[1,0],[0,1]:
> display(polygon([karjet],filled=true,color=yellow));
![[Maple Plot]](images/harj10lv7.gif)
>
Mieti kuvien rakentelu "seinittäin". Kokeile vaikka seinä kerrallaan displayta.
Sama tyyli toistuu miltei kaikissa. Seinät ovat parametrimuotoisia pintoja, 2 parametria, joista toinen on z.
3.
> suora:=solve(2*x+2*y=5,y); # Silkkaa laiskuutta!
![]()
> plot([suora,1/x],x=0..3,y=0..3);
![[Maple Plot]](images/harj10lv9.gif)
> hypseina:=plot3d([x,1/x,z],x=0.5..2,z=0..ln(x),labels=[x,y,z]):
> suoraseina:=plot3d([x,suora,z],x=0.5..2,z=0..ln(x),labels=[x,y,z]):
> display(hypseina,suoraseina,plot3d(ln(x),x=0.5..2,y=1/x..suora),style=patchcontour);
![[Maple Plot]](images/harj10lv10.gif)
Kyseessä on kuvassa näkyvien kuppien tilavuuksien erotus.
4.
> parseina:=plot3d([x,x^2,z],x=0..2,z=0..exp(x^2/x),labels=[x,y,z]):
> suoraseina:=plot3d([x,2*x,z],x=0..2,z=0..exp(2*x/x),labels=[x,y,z]):
> display(parseina,suoraseina,plot3d(exp(y/x),x=0..2,y=x^2..2*x,color=red),style=patch);
![[Maple Plot]](images/harj10lv11.gif)
> plot3d(exp(y/x),x=0..2,y=x^2..2*x,style=patchcontour);
![[Maple Plot]](images/harj10lv12.gif)
>
5.
> restart:
Warning, the name changecoords has been redefined
> x:=r*cos(Theta);y:=r*sin(Theta);
![]()
![]()
> r:=2*sqrt(cos(2*Theta));
![]()
![]() -taso:
-taso:
> plot(r,Theta=-Pi/4..Pi/4,labels=['Theta','r']);
![[Maple Plot]](images/harj10lv17.gif)
> plot([x,y,Theta=-Pi/4..Pi/4]);
![[Maple Plot]](images/harj10lv18.gif)
>
6.
> restart:
Warning, the name changecoords has been redefined
> with(plots):
> z1:=x^2+y^2; z2:=(4-x^2-y^2)/3;
![]()
![]()
> x:=r*cos(Theta); y:=r*sin(Theta);
![]()
![]()
> ala:=plot3d([x,y,z1],r=0..1,Theta=0..2*Pi):
> yla:=plot3d([x,y,z2],r=0..1,Theta=0..2*Pi):
> display(ala,yla,style=patchcontour);
![[Maple Plot]](images/harj10lv23.gif)
>
Loppviikko:
Piirtäminen menee samaan tyyliin kuin AV.
Laskemiseen on esimerkkejä int23d.mws :ssä. Hyvä tyyli on
> restart:
Warning, the name changecoords has been redefined
> Int(Int(int(f(x,y,z),z=c1(x,y)..c2(x,y)),y=b1(x)..b2(x)),x=a1..a2):
> %=value(%);
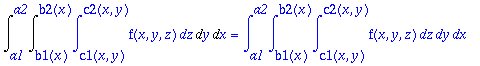
Tässä ei mitään laskentaa voinut tapahtua.
>
1.
>
restart:with(plots):with(plottools):
setoptions3d(axes=boxed,orientation=[-30,50]):
Warning, the name changecoords has been redefined
Warning, the name arrow has been redefined
> display(implicitplot(abs(2*x+3*y)=4,x=-2.5..2.5,y=-2..2,color=blue),implicitplot(abs(x-5*y)=3,x=-3..3,y=-2..2));
![[Maple Plot]](images/harj10lv25.gif)
Voidaan käyttää myös plots[inequal] -funktiota. Siinä valitsin feasible on lineaarisen optimoinnin terminologiaa.
>
inequal( { 2*x+3*y <=4,2*x+3*y >=-4, (x-5*y)<=3,(x-5*y)>=-3}, x=-3..3, y=-2..2,optionsfeasible=(color=yellow), optionsexcluded=(color=white) );
![[Maple Plot]](images/harj10lv26.gif)
> solve({2*x+3*y=u,x-5*y=v},{x,y});
![]()
> subs(%,[x,y]);linalg[jacobian](%,[u,v]);
![]()
![matrix([[5/13, 3/13], [1/13, -2/13]])](images/harj10lv29.gif)
> linalg[det](%);abs(%);
![]()
![]()
> muuntosuhde:=%;
![]()
Muuttujanvaihtokuvaus on lineaarinen, joten jakobiaani (niin matriisi kuin det) on vakio. Niinpä meillä on vakio muuntosuhde, joka voidaan ottaa integraalissa suoraan eteen tekijäksi.
> muuntosuhde*int(int(u^2*v^2,v=-3..3),u=-4..4);evalf(%);
![]()
![]()
2.
>
restart:with(plots):with(plottools):
setoptions3d(axes=boxed,orientation=[-30,50]):
Warning, the name changecoords has been redefined
Warning, the name arrow has been redefined
> z:=c*(1-x/a-y/b);a:=1:b:=2:c:=3:
![]()
>
plot3d(z,x=0..a,y=0..b*(1-x/a),axes=box,style=patchcontour);
![[Maple Plot]](images/harj10lv36.gif)
Voidaan käyttää myös spesiaalimpaa polygonipiirtoa:
Error, missing operator or `;`
>
tahko1:=polygon([[a,0,0],[0,b,0],[0,0,c]],color=gold):
tahko2:=polygon([[0,0,0],[0,b,0],[0,0,c]],color=yellow):
tahko3:=polygon([[0,0,0],[0,b,0],[a,0,0]],color=cyan):
tahko4:=polygon([[0,0,0],[0,0,c],[a,0,0]],color=gray):
display([tahko1,tahko2,tahko3,tahko4],axes=boxed,labels=['x','y','z']);
![[Maple Plot]](images/harj10lv37.gif)
> a:='a':b:='b':c:='c':z:='z':
> Int(Int(Int(x,z=0..c*(1-x/a-y/b)),y=0..b*(1-x/a)),x=0..a):%=value(%);
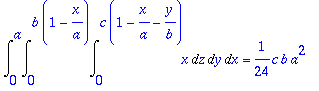
3.
> restart:with(linalg):
Warning, the name changecoords has been redefined
Warning, the protected names norm and trace have been redefined and unprotected
>
x:=rho*sin(phi)*cos(Theta);
y:=rho*sin(phi)*sin(Theta);
z:=rho*cos(phi);
![]()
![]()
![]()
> jacobian([x,y,z],[rho,Theta,phi]);
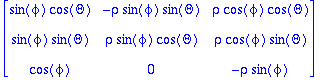
> det(%);simplify(%);abs(%);
![]()
![]()
![]()
Maple ei tietenkään tiedä, että 0 <= phi <= Pi, jolloin sin(phi) >= 0. Me tiedämme!
4.
>
restart: with(plots):z1:=sqrt(x^2+y^2);
Warning, the name changecoords has been redefined
![]()
Tapa 1: Lasketaan tasointegraalina napakoordinaatistossa:
>
z1:=r;z2:=sqrt(a^2-r^2);R:=solve(z1=z2,r);a:=2; x:=r*cos(Theta):y:=r*sin(Theta);
R;z1;z2;
kartio:=plot3d([x,y,z1],Theta=0..2*Pi,r=0..R):
pallo:=plot3d([x,y,z2],Theta=0..2*Pi,r=0..R):
display([kartio,pallo],style=patchcontour);
a:='a':V:=Int(Int((z2-z1)*r,r=0..a/sqrt(2)),Theta=0..2*Pi): %=simplify(value(%),symbolic);
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Maple Plot]](images/harj10lv55.gif)
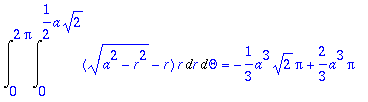
Tapa 2. Lasketaan tilavuus pallokoordinaatistossa.
Tässä on käyetty sellaista tyyliä, että homma on aina ajettava alusta (tästä) asti , "välistävedot" menevät
yleensä virheeseen, koska muuttujat on vapautettava ja sitten sidottava pallokoordinaatteihin, kuten tässä alussa tehdään. (Voitaisiin toteuttaa toisinkin, mutta tämä on nopea (ja tässä mielessä hutera) tapa.)
>
phi:='phi';rho:='rho':x:=rho*sin(phi)*cos(Theta);
y:=rho*sin(phi)*sin(Theta);
z:=rho*cos(phi);
rho:=a:phi:='phi';
![]()
![]()
![]()
![]()
![]()
>
a:=2:jatski:=plot3d([x,y,z],Theta=0..2*Pi,phi=0..Pi/4):
rho:='rho': phi:=Pi/4:
>
tottero:=plot3d([x,y,z],Theta=0..2*Pi,rho=0..a):
display(jatski,tottero,style=patchnogrid);
![[Maple Plot]](images/harj10lv62.gif)
>
tottero;
a:='a':phi:='phi':Theta:='Theta':
![[Maple Plot]](images/harj10lv63.gif)
>
V:=Int(Int(Int(r^2*sin(phi),phi=0..Pi/4),theta=0..2*Pi),r=0..a);value(%);
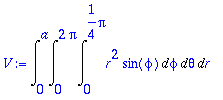
![]()
5.
Täytyy siirtää tuonnemmaksi, tässä ei pitäisi olla mitään konstikasta.
6.
> restart:with(plots):
Warning, the name changecoords has been redefined
Pallokoordinaattiesitys antaa luontevan pallopinnan parametriesityksen. Siinä säde
rho on vakio ja parametreina ovat leveyskulma Theta ja korkeuskulma phi . Edellinen menee [ 0 .. 2*Pi] ja jälkimmäinen [0 .. Pi] .
Kirjoitetaan proc:ksi, joka palauttaa rho-säteisen pallon parametriesityksen:
>
pallopinta:=proc(rho)
local x,y,z;
x:=rho*sin(phi)*cos(Theta);
y:=rho*sin(phi)*sin(Theta);
z:=rho*cos(phi);
[x,y,z]
end:
>
pallopinta(2*a);
![]()
>
pallo:=plot3d(pallopinta(2),Theta=0..2*Pi,phi=0..Pi,style=patch,scaling=constrained):
Lieriö on luontevinta esittää siirretyissä lieriökoordinaateissa, jossa origona on piste (0,a). Parametreina siis tämän origon
suhteen otettu napakulma ja z.
> lierio:=plot3d([cos(Theta),1+sin(Theta),z],Theta=0..2*Pi,z=-2..2,color=red,labels=["x","y","z"]):
> display(pallo,lierio,axes=box);
![[Maple Plot]](images/harj10lv67.gif)
Entä, jos haluamme katsoa lieriötä ja sen kattoa ja pohjaa, ts. sitä varsinaista kappaletta.
> a:=1:ylapinta:=plot3d([r*cos(Theta),r*sin(Theta),sqrt(4*a^2-r^2)],Theta=0..Pi,r=0..2*a*sin(Theta),scaling=constrained,axes=box,color=red):
> alapinta:=plot3d([r*cos(Theta),r*sin(Theta),-sqrt(4*a^2-r^2)],Theta=0..Pi,r=0..2*a*sin(Theta),scaling=constrained,axes=box,color=blue):
> lierio:=plot3d([cos(Theta),1+sin(Theta),z],Theta=0..2*Pi,z=-1.8..1.7,color=yellow,labels=["x","y","z"]):
> display(lierio,ylapinta,alapinta,style=patch);
![[Maple Plot]](images/harj10lv68.gif)
>
Piirrettiin lieriö hiukan matalammaksi, jotta kansi ja pohja paremmin pilkistävät.
Luentotehtävän tyylinen: Reikäpallon hitausmomentti
Laitan tähän lisäharjoittelua ajatellen. Pallon säde = a. Porataan keskeltä läpi lieriöreikä, jonka säde = b
(b < a). Olkoon pallon tiheys = delta = vakio. Laskettava reikäpallon hitausmomentti z-akselin suhteen.
Lisäharjoitus: Määritä rajat pallokoordinaateissa (tein luennolla, lasku tulee epäilemättä mutkikkaammaksi.
> restart: setoptions3d(axes=boxed,orientation=[-30,50]):with(plots):
Warning, the name changecoords has been redefined
> 2*delta*Int(Int(Int(r,z=0..sqrt(a^2-r^2)),r=b..a),Theta=0..2*Pi);
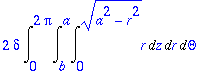
> massa:=value(%);
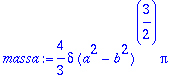
>
> 2*delta*Int(Int(Int(r*r^2,z=0..sqrt(a^2-r^2)),r=b..a),Theta=0..2*Pi);
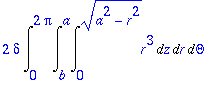
> J:=simplify(value(%),symbolic);
![]()
Jos vielä lausutaan massan avulla, saadaan varsin sievä muoto:
> J/massa;
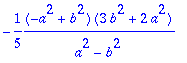
> J:=simplify(%*m);
![]()
Sitten piirretään:
> zala:=-sqrt(a^2-r^2);zyla:=sqrt(a^2-r^2):
![]()
> x:=r*cos(Theta):y:=r*sin(Theta):
> a:=2:b:=0.8:
> reikapallo:=display(plot3d([x,y,zyla],r=b..a,Theta=0..2*Pi,style=patchnogrid),plot3d([x,y,zala],r=b..a,Theta=0..2*Pi,style=patchnogrid)):
> lierio:=plot3d([b*cos(Theta),b*sin(Theta),z],Theta=0..2*Pi,z=-a..a):
> reikapallo;display(reikapallo,lierio);
![[Maple Plot]](images/harj10lv76.gif)
![[Maple Plot]](images/harj10lv77.gif)
>
>