Harj. 10 AV
7.4.02 HA
Alustukset
> restart:
Warning, the name changecoords has been redefined
> with(LinearAlgebra): with(plots): alias(Tr=Transpose,Lsolve=LinearSolve):
> with(linalg):with(plottools):
Warning, the previous binding of the name GramSchmidt has been removed and it now has an assigned value
Warning, the protected names norm and trace have been redefined and unprotected
Warning, the name arrow has been redefined
>
setoptions3d(axes=boxed,orientation=[-30,50]):
> V2L:=vek->convert(vek,list):
> #read("/home/apiola/opetus/peruskurssi/v2-3/maple/v202.mpl");
1.
> f:=x*y^2+y^3;
![]()
> pinta:=plot3d(f,x=0..2,y=1..3,view=[0..2,1..3,0..50]):
> Int(Int(f,y=1..3),x=0..2): %=value(%);
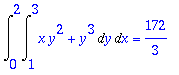
Käsin laskien päästiin tähän x-integraaliin, joka annetaan juhlallisesti Maplen laskettavaksi. Saadaan jopa sama tulos!
> int((9-1/3)*x+3^4/4-1/4,x=0..2);
![]()
Voidaan tehdä myös vaiheittain laskemalla ensin integrointi y:n suhteen ja antamalla oikella puolella value-komennon hoitaa myös x-integrointi:
> Int(int(f,y=1..3),x=0..2): %=value(%);
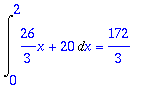
> F:=unapply(f,x,y); fv:=x->F(x[1],x[2]);
![]()
![]()
> pohja:=[[0,1],[2,1],[2,3],[0,3]];pohja3d:=[[0,1,0],[2,1,0],[2,3,0],[0,3,0]];
![]()
![]()
> kansiz:=map(fv,pohja);
![]()
> kansi3d:=zip((x,y)->[op(x),y],pohja,kansiz); # Eleganttia!
![]()
> display(polygon(pohja3d),polygon([pohja3d[1],kansi3d[1],kansi3d[2],pohja3d[2]]),polygon([pohja3d[3],kansi3d[3],kansi3d[4],pohja3d[4]]),pinta,axes=none,style=patchnogrid);
![[Maple Plot]](images/harj10av11.gif)
2.
> karjet:=[-1,0],[1,0],[0,1]:
> display(polygon([karjet],filled=true,color=yellow));
![[Maple Plot]](images/harj10av12.gif)
y-proj: laskettava 2:ssa osassa:
> vasen:=Int(Int(x*y+y^2,y=0..x+1),x=-1..0):
> oikea:=Int(Int(x*y+y^2,y=0..-x+1),x=0..1):
> vasen+oikea=value(vasen+oikea);
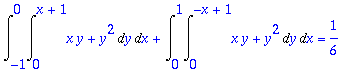
>
3.
> plot([solve(2*x+2*y=5,y),1/x],x=0..3,y=0..3);
![[Maple Plot]](images/harj10av14.gif)
> solve({x+y=5/2,x*y=1},{x,y});
![]()
> hypseina:=plot3d([x,1/x,z],x=0.5..2,z=0..ln(x),labels=[x,y,z]):
> suora:=solve(2*x+2*y=5,y);
![]()
> suoraseina:=plot3d([x,suora,z],x=0.5..2,z=0..ln(x),labels=[x,y,z]):
> display(hypseina,suoraseina,plot3d(ln(x),x=0.5..2,y=1/x..suora),style=patchcontour);
![[Maple Plot]](images/harj10av17.gif)
> Int(Int(ln(x),y=1/x..suora),x=1/2..2);
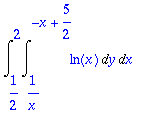
> %=value(%);
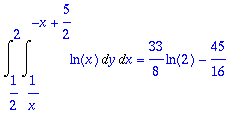
> evalf(rhs(%));
![]()
Kyseessä on kuvassa näkyvien kuppien tilavuuksien erotus.
4.
> parseina:=plot3d([x,x^2,z],x=0..2,z=0..exp(x^2/x),labels=[x,y,z]):
> suoraseina:=plot3d([x,2*x,z],x=0..2,z=0..exp(2*x/x),labels=[x,y,z]):
> display(parseina,suoraseina,plot3d(exp(y/x),x=0..2,y=x^2..2*x),style=patch);
![[Maple Plot]](images/harj10av21.gif)
> plot3d(exp(y/x),x=0..2,y=x^2..2*x,style=patchcontour);
![[Maple Plot]](images/harj10av22.gif)
> int(x*(exp(2)-exp(x)),x=0..2);
![]()
> Int(Int(exp(y/x),x=y/2..sqrt(y)),y=0..4);
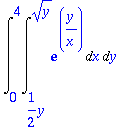
> %=value(%);
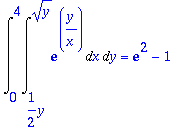
> Int(Int(exp(y/x),y=x^2..2*x),x=0..2);
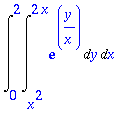
> value(%);
![]()
>
5.
> restart:
Warning, the name changecoords has been redefined
> f:=Theta->2*sqrt(cos(2*Theta));
![]()
>
> plot(f,-Pi/4..Pi/4,labels=['Theta','r']);
![[Maple Plot]](images/harj10av29.gif)
> x:=r*cos(Theta);y:=r*sin(Theta);
![]()
![]()
> r:=f(Theta);
![]()
> x,y;
![]()
> plot([x,y,Theta=-Pi/4..Pi/4]);
![[Maple Plot]](images/harj10av34.gif)
> plot([x,y,Theta=-Pi..Pi]);
![[Maple Plot]](images/harj10av35.gif)
> f:=Theta->2*sqrt(abs(cos(2*Theta)));
![]()
> plot([x,y,Theta=-Pi/4..Pi/4]);plot([x,y,Theta=-Pi..Pi]);
![[Maple Plot]](images/harj10av37.gif)
![[Maple Plot]](images/harj10av38.gif)
>
6.
> restart:
Warning, the name changecoords has been redefined
> with(plots):
> z1:=x^2+y^2; z2:=(4-x^2-y^2)/3;
![]()
![]()
> x:=r*cos(Theta); y:=r*sin(Theta);
![]()
![]()
> ala:=plot3d([x,y,z1],r=0..1,Theta=0..2*Pi):
> yla:=plot3d([x,y,z2],r=0..1,Theta=0..2*Pi):
> display(ala,yla,style=patchcontour);
![[Maple Plot]](images/harj10av43.gif)
>
>