Harj. 6 LV
pe 8.3.02 HA
Alustukset
> restart:
Warning, the name changecoords has been redefined
> with(LinearAlgebra): with(linalg):
Warning, the previous binding of the name GramSchmidt has been removed and it now has an assigned value
Warning, the protected names norm and trace have been redefined and unprotected
> alias(Inv=MatrixInverse,IdM=IdentityMatrix,Diag=DiagonalMatrix,Tr=Transpose):
> with(plots): with(plottools):
Warning, the name arrow has been redefined
>
V2L:=vek->convert(vek,list):
v2l:=vek->convert(vek,list):
L2V:=lis->convert(lis,Vector):
l2v:=lis->convert(lis,vector):
> jana3dpv:=(p,v)->spacecurve([p,V2L(Vector(p)+Vector(v))],thickness=2,color=blue):
1.
> f:=(x,y)->arctan(y/x);
![]()
> x0:=2:y0:=2;
![]()
>
T:=f(x0,y0)+D[1](f)(x0,y0)*(x-x0)+D[2](f)(x0,y0)*(y-y0);
![]()
>
subs(x=x0,y=y0,T);
f(2,2);
![]()
![]()
> hpmax:=1.5:htmax:=0.8:
>
pinta:=plot3d(f(x,y),x=x0-hpmax..x0+hpmax,y=y0-hpmax..y0+hpmax,style=patchcontour):
>
taso:=plot3d(T,x=x0-htmax..x0+htmax,y=y0-htmax..y0+htmax,style=PATCH,color=red,grid=[7,7]):
> display(pinta,taso);
![[Maple Plot]](images/harj6lv6.gif)
>
N:=[D[1](f)(x0,y0),D[2](f)(x0,y0),-1];
![]()
>
display(pinta,taso,jana3dpv([x0,y0,f(x0,y0)],N),jana3dpv([x0,y0,f(x0,y0)],-N));
![[Maple Plot]](images/harj6lv8.gif)
Pinta, tangenttitaso ja normaali (pyörittele vähän, niin näkyy paremmin).
2 ja 3.
> A:=<<1/2,1/4,1/4>|<1/4,1/2,1/4>|<1/4,1/4,1/2>>;
![A := _rtable[134830436]](images/harj6lv9.gif)
> A-Tr(A);
![_rtable[135849844]](images/harj6lv10.gif)
Olishan tuon nähnyt päältäpäinkin.
Koska matriisi on symmetrinen , niin peruslause => ominaisvekroreista voidaan muodostaa ortonormaali kanta.
> p:=det(A-lambda*IdM(3));factor(p);# Karakteristinen polynomi
![]()
![]()
>
lam:=solve(%=0,lambda);
![]()
>
M1:=A-lam[1]*IdM(3);
M2:=A-lam[2]*IdM(3);
![M1 := _rtable[136345908]](images/harj6lv14.gif)
![M2 := _rtable[135330384]](images/harj6lv15.gif)
>
gaussjord(M1),gaussjord(M2);
![matrix([[1, 0, -1], [0, 1, -1], [0, 0, 0]]), matrix...](images/harj6lv16.gif)
![]()
x3 voidaan valita vapaasti, esim. x3=1. x2=x1 (=1), x3=x1 (=1). Siis ominaisvektori [1,1,1] ja normeerattuna:
> X1:=1/sqrt(3)*<1,1,1>;
![X1 := _rtable[136338576]](images/harj6lv18.gif)
![lambda[2] = 1/4](images/harj6lv19.gif) . x3 ja x2 voidaan valita vapaasti: x1 = -x2 - x3.
. x3 ja x2 voidaan valita vapaasti: x1 = -x2 - x3.
Saadaan 2 LRV ominaisvektoria valitsemalla a) x2=1, x3 =0 => x1=-1 ja b) x2=0, x3=1 => x1=-1, eli:
> X2:=1/sqrt(2)*<-1,1,0>;X3:=1/sqrt(2)*<-1,0,1>;
![X2 := _rtable[136338696]](images/harj6lv20.gif)
![X3 := _rtable[136338816]](images/harj6lv21.gif)
Tehtävä 2 on valmis (ja vähän ylikin, ei siinä pyydetty edes normeerausta).
> Tr(X1).X2;Tr(X1).X3;
![]()
![]()
Teorian mukaan eri ominaisarvoihin liittyvät ominaisvektorit ovat ortogonaaliset, joten näin käy aina (jos oikein laskettu).
Sensijaan kaksinkertaiseen ominaisarvoon liittyvät ominaisvektorit eivät ole automaattisesti ortogonaaliset.
Ortogonaalinen kanta saadaan ajattelemalla geometrisen havainnollisesti: Projisioidaan toinen vektori toiselle ja vähennetää tämä projektiovektori. Normeerataan ensin (sehän jo tehtiin), jolloin kaava tulee yksinkertaiseen muotoon:
X2 - (X2,X3)X3
> V2:=X2-(Tr(X2).X3).X3;
![V2 := _rtable[135983900]](images/harj6lv24.gif)
> Tr(V2).X3;
![]()
> X2:=V2/Norm(V2,2);
![X2 := _rtable[136317212]](images/harj6lv26.gif)
> X:=<X1|X2|X3>;
![X := _rtable[135299860]](images/harj6lv27.gif)
> Tr(X).X;
![_rtable[136334904]](images/harj6lv28.gif)
Käsin laskettuna saattoi olla hieman vaikea, kun ortogonalsiointitekniikkaa ei ole kunnolla esitelty. Sinänsä, kun tämän on ajatellut havainnollisesti, asia on hyvin luonteva.
Sovitaanpa, että j os tällainen tehtävä tulee kokeeseen, niin tuo projektiokaava ohjeineen annetaan.
Maplella automaattisemmin
> omsys:=Eigenvectors(A);
![omsys := _rtable[136536220], _rtable[136675720]](images/harj6lv29.gif)
> V:=omsys[2];
![V := _rtable[136675720]](images/harj6lv30.gif)
Kaksi ensimmäistä vektoria eivät taaskaan ole ortogonaalisia. Help:stä löytyy GramScmidt (edellyttää tämän yhdistelmän assosiontia ortogonalisointiin).
Kaiken lisäksi GramScmidt näkyy toimivan versiossa 7, mutta ei 6:ssa. (Helppiesimerkki (cut/paste) menee virheseen.)
Antaapa sen nyt siis olla ja todetaan, että loppu tehdään, kuten yllä.
> #?LinearAlgebra
>
> GramSchmidt([<-1,1,0>,<-1,0,1>]); # Eipä toimi, linalg:n vastaava varmasti toimii, mutta olkoonpa nyt.
Error, (in GramSchmidt) 1st argument must be a non-empty list or set of vectors
Error, (in GramSchmidt) 1st argument must be a non-empty list or set of vectors
4.
a)
> q:=2*x1^2+4*x2^2+x1*x2;
![]()
> A:=<<2,1/2>|<1/2,4>>;
![A := _rtable[138567972]](images/harj6lv32.gif)
> x:=<x1,x2>;
![x := _rtable[136867524]](images/harj6lv33.gif)
> Tr(x).A.x;expand(%);
![]()
![]()
Oikein on. Katsotaan vielä Hessian ja pannaan vierelle 2*A
> hessian(q,[x1,x2]),2*A; # hessian asustaa vanhassa linalg:ssa
![matrix([[4, 1], [1, 8]]), _rtable[136862868]](images/harj6lv36.gif)
> Eigenvalues(A);
![_rtable[136092820]](images/harj6lv37.gif)
> omsys:=Eigenvectors(A);
![omsys := _rtable[135840360], _rtable[135494232]](images/harj6lv38.gif)
> eigenvectors(A);
![]()
> DD:=Diag(omsys[1]);
![DD := _rtable[135401676]](images/harj6lv40.gif)
> X1:=omsys[2][1..2,1]: X1:=X1/Norm(X1,2):X1:=map(simplify,%);
![X1 := _rtable[136846332]](images/harj6lv41.gif)
> Norm(X1,2);simplify(%);
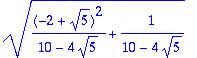
![]()
> X2:=omsys[2][1..2,2]: X2:=X2/Norm(X2,2):X2:=map(simplify,%);
![X2 := _rtable[138283164]](images/harj6lv44.gif)
> X:=<X1|X2>;
![X := _rtable[137239548]](images/harj6lv45.gif)
> XT:=Tr(X);
![XT := _rtable[134901924]](images/harj6lv46.gif)
> A-map(simplify,X.DD.XT);map(simplify,%);
![_rtable[136747032]](images/harj6lv47.gif)
![_rtable[136739496]](images/harj6lv48.gif)
> Q:=<y1|y2>.DD.<y1,y2>;
![]()
> implicitplot(q=1,x1=-2..2,x2=-2..2,grid=[50,50]);
![[Maple Plot]](images/harj6lv50.gif)
> implicitplot(Q=1,y1=-2..2,y2=-2..2,grid=[50,50]);
![[Maple Plot]](images/harj6lv51.gif)
>
>
b)
> A:=<<0,1,0>|<1,0,1>|<0,1,1>>;
![A := _rtable[135574432]](images/harj6lv52.gif)
> <x1|x2|x3>.A.<x1,x2,x3>;q:=expand(%);
![]()
![]()
> p:=det(A-lambda*IdM(3));
![]()
> lam:=fsolve(p=0,lambda);
![]()
> Q:=lam[1]*y1^2+lam[2]*y2^2+lam[3]*y3^2;
![]()
> implicitplot3d(Q=1,y1=-2..2,y2=.2..2,y3=-2..2);
![[Maple Plot]](images/harj6lv58.gif)
>
>
> A:=<<0,1,0>|<1,0,1>|<0,1,1.>>;
![A := _rtable[134956492]](images/harj6lv59.gif)
> lam:=Eigenvalues(A);
![lam := _rtable[136768548]](images/harj6lv60.gif)
> map(Im,lam);lam:=map(Re,lam);
![_rtable[138648628]](images/harj6lv61.gif)
![lam := _rtable[138653188]](images/harj6lv62.gif)
> Q:=<y1|y2|y3>.Diag(lam).<y1,y2,y3>;
![]()
c)
> A:=<<1,0,0,0>|<0,0,-2,0>|<0,-2,0,0>|<0,0,0,2>>;
![A := _rtable[137212984]](images/harj6lv64.gif)
> <x1|x2|x3|x4>.A.<x1,x2,x3,x4>;
![]()
> lam:=Eigenvalues(A);
![lam := _rtable[136756996]](images/harj6lv66.gif)
> Q:=add(lam[k]*y[k]^2,k=1..4);
![]()
> sum(lam[k]*y[k]^2,k=1..4); # mystistä!
Error, bad index into Vector
> lam[4]; # Vektorin indekseissä ei ole oikeasti vikaa, toimiihan myös add.
![]()
> ll:=convert(lam,list);
![]()
> sum(ll[i]*y[i]^2,i=1..4);
![]()
Listaksi konversion jälkeen toimii. "Bad index into vector" on tosi outo juttu, mutta olkoonpa nyt.
5.
> A:=<<1,12>|<12,-6>>;
![A := _rtable[137822748]](images/harj6lv71.gif)
> q:=expand(<x1|x2>.A.<x1,x2>);
![]()
> (lam,X):=Eigenvectors(A);
![lam, X := _rtable[138590416], _rtable[137225664]](images/harj6lv73.gif)
> normit:=Norm(X[1..2,1],2),Norm(X[1..2,2],2);
![]()
> X:=X/normit[1]; # koska kerran samoja
![X := _rtable[137424076]](images/harj6lv75.gif)
> Inv(X), Tr(X); # Ovat samoja (hyvä aina tarkistaa).
![_rtable[137567964], _rtable[137545280]](images/harj6lv76.gif)
> y1:=(1/sqrt(3))*sinh(t);y2p:=(1/sqrt(2))*cosh(t);y2m:=-y2p;
![]()
![]()
![]()
> pos:=plot([y1,y2p,t=-2..2],view=[-4..4,-4..4],scaling=constrained):
> neg:=plot([y1,y2m,t=-2..2],view=[-4..4,-4..4],scaling=constrained):
> display(pos,neg);
![[Maple Plot]](images/harj6lv80.gif)
> x1x2p:=X.<y1,y2p>;
![x1x2p := _rtable[135578928]](images/harj6lv81.gif)
> x1x2m:=X.<y1,y2m>;
![x1x2m := _rtable[136299760]](images/harj6lv82.gif)
> phaara:=plot([op(V2L(x1x2p)),t=-3..3],x1=-8..8,x2=-8..8):
> nhaara:=plot([op(V2L(x1x2m)),t=-3..3]):
> display(phaara,nhaara);
![[Maple Plot]](images/harj6lv83.gif)
> implicitplot(q=5,x1=-8..8,x2=-8..8,grid=[50,50]);
![[Maple Plot]](images/harj6lv84.gif)
>
>
> V2L(x1x2p);
![]()
>
>