Tässä yksi tapa eli minun tapani ratkaista kuudennet mikroharjoitukset.
Markko
Input := <<Algebra`SymbolicSum`
Input :=
Sum[1/((k-1)(k+1)),{k,2,Infinity}]
Output = 3 - 4
Input :=
Sum[1/((k-1)(2k+1)),{k,2,Infinity}]
Output =
2 (4 - 3 Log[2])
----------------
9
Input :=
Sum[1/((k^2-1)(k^2+1)),{k,2,Infinity}]
Output = 7 Pi Coth[Pi] - - ----------- 8 4
Input :=
Sum[1/k^1,{k,1,Infinity}]
Output = Infinity
Input :=
Sum[1/k^2,{k,1,Infinity}]
Output = 2 Pi --- 6
Input :=
Sum[1/k^3,{k,1,Infinity}]
Output = Zeta[3]
Input :=
Sum[1/k^4,{k,1,Infinity}]
Output = 4 Pi --- 90
Input :=
Sum[1/k^alfa,{k,1,Infinity}]
Output = Zeta[alfa]
Input := Zeta[0]
Output = 1 -(-) 2
Input := Zeta[1]
Output = ComplexInfinity
Input := ?Series
Series[f, {x, x0, n}] generates a power series expansion for f
about the point x = x0 to order (x - x0)^n. Series[f, {x,
x0, nx}, {y, y0, ny}] successively finds series expansions
with respect to y, then x.
Input :=
Series[ArcTan[x],{x,0,5}]
Output =
3 5
x x 6
x - -- + -- + O[x]
3 5
Input :=
Series[ArcTan[x],{x,0,10}]
Output =
3 5 7 9
x x x x 11
x - -- + -- - -- + -- + O[x]
3 5 7 9
Input :=
Series[ArcTan[x],{x,0,20}]
Output =
3 5 7 9 11 13 15 17 19
x x x x x x x x x 21
x - -- + -- - -- + -- - --- + --- - --- + --- - --- + O[x]
3 5 7 9 11 13 15 17 19
Input :=
Plot[Evaluate[{ArcTan[x],Normal[%19],Normal[%20],Normal[%21]}]
,{x,-5,5},PlotRange->{-5,5}]
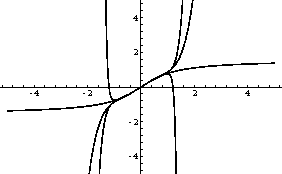
Output = -Graphics-
Input :=
SymbolicSum[x^k/k,{k,1,Infinity}]
Output = -Log[1 - x]
Input :=
Plot[{Sum[x^k/k,{k,1,10}],-Log[1-x]},{x,-5,5},PlotRange->{-7,7}]
Plot::plnr: CompiledFunction[{x}, <<1>>, -CompiledCode-][x]
is not a machine-size real number at x = 1.25.
Plot::plnr: CompiledFunction[{x}, <<1>>, -CompiledCode-][x]
is not a machine-size real number at x = 1.04167.
Plot::plnr: CompiledFunction[{x}, <<1>>, -CompiledCode-][x]
is not a machine-size real number at x = 1.01563.
General::stop:
Further output of Plot::plnr
will be suppressed during this calculation.
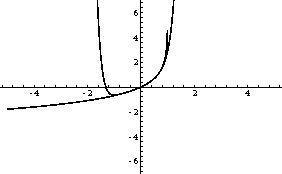
Output = -Graphics-
Input :=
SumbolicSum[Cos[k^2x]/k^2,{k,1,Infinity}]
Output =
2
Cos[k x]
SumbolicSum[---------, {k, 1, Infinity}]
2
k
Input :=
Plot[Sum[Cos[k^2x]/k^2,{k,1,20}],{x,-5,5},PlotRange->{-2,2}]
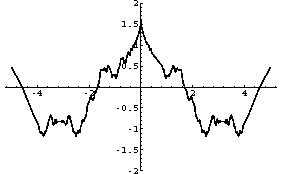
Output = -Graphics-
Input :=
Series[Cos[x],{x,0,10}] * (Sum[a[k] x^k, {k,0,10}] + O[x]^11 )
Output =
-a[0] 2 -a[1] 3
a[0] + a[1] x + (----- + a[2]) x + (----- + a[3]) x +
2 2
a[0] a[2] 4 a[1] a[3] 5
(---- - ---- + a[4]) x + (---- - ---- + a[5]) x +
24 2 24 2
-a[0] a[2] a[4] 6
(----- + ---- - ---- + a[6]) x +
720 24 2
-a[1] a[3] a[5] 7
(----- + ---- - ---- + a[7]) x +
720 24 2
a[0] a[2] a[4] a[6] 8
(----- - ---- + ---- - ---- + a[8]) x +
40320 720 24 2
a[1] a[3] a[5] a[7] 9
(----- - ---- + ---- - ---- + a[9]) x +
40320 720 24 2
-a[0] a[2] a[4] a[6] a[8] 10 11
(------- + ----- - ---- + ---- - ---- + a[10]) x + O[x]
3628800 40320 720 24 2
Input := LogicalExpand[%39==1]
Output =
-a[0]
-1 + a[0] == 0 && a[1] == 0 && ----- + a[2] == 0 &&
2
-a[1] a[0] a[2]
----- + a[3] == 0 && ---- - ---- + a[4] == 0 &&
2 24 2
a[1] a[3]
---- - ---- + a[5] == 0 &&
24 2
-a[0] a[2] a[4]
----- + ---- - ---- + a[6] == 0 &&
720 24 2
-a[1] a[3] a[5]
----- + ---- - ---- + a[7] == 0 &&
720 24 2
a[0] a[2] a[4] a[6]
----- - ---- + ---- - ---- + a[8] == 0 &&
40320 720 24 2
a[1] a[3] a[5] a[7]
----- - ---- + ---- - ---- + a[9] == 0 &&
40320 720 24 2
-a[0] a[2] a[4] a[6] a[8]
------- + ----- - ---- + ---- - ---- + a[10] == 0
3628800 40320 720 24 2
Input := Solve[%]
Output =
50521 277
{{a[9] -> 0, a[10] -> -------, a[7] -> 0, a[8] -> ----,
3628800 8064
61 5
a[5] -> 0, a[6] -> ---, a[3] -> 0, a[4] -> --, a[1] -> 0,
720 24
1
a[2] -> -, a[0] -> 1}}
2
Input :=
Sum[a[k] x^k, {k,0,10}] /. %
Output =
2 4 6 8 10
x 5 x 61 x 277 x 50521 x
{1 + -- + ---- + ----- + ------ + ---------}
2 24 720 8064 3628800
Input :=
Series[1/Cos[x],{x,0,10}]
Output =
2 4 6 8 10
x 5 x 61 x 277 x 50521 x 11
1 + -- + ---- + ----- + ------ + --------- + O[x]
2 24 720 8064 3628800
Input :=
1/Series[Cos[x],{x,0,10}]
Output =
2 4 6 8 10
x 5 x 61 x 277 x 50521 x 11
1 + -- + ---- + ----- + ------ + --------- + O[x]
2 24 720 8064 3628800
Input :=
Series[x+Sin[x],{x,0,10}]
Output =
3 5 7 9
x x x x 11
2 x - -- + --- - ---- + ------ + O[x]
6 120 5040 362880
Input :=
Plot[x+Sin[x],{x,-4Pi,4Pi}]
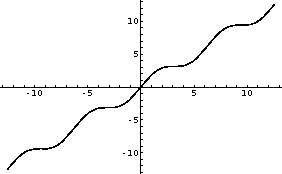
Output = -Graphics-
Input := InverseSeries[%49]
Output =
3 5 7 9
x x x 43 x 223 x 11
- + -- + ---- + ------- + -------- + O[x]
2 96 1920 1290240 92897280
Input := Normal[%57]
Output =
3 5 7 9
x x x 43 x 223 x
- + -- + ---- + ------- + --------
2 96 1920 1290240 92897280
Input :=
Plot[%59,{x,-10,10},PlotRange->{-20,20}]
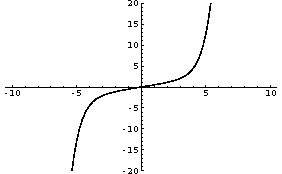
Output = -Graphics-
Input :=
ParametricPlot[{x+Sin[x],x},{x,-10,10},PlotRange->{-20,20}]
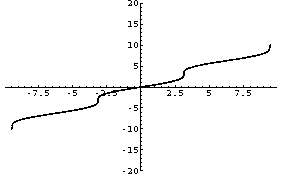
Output = -Graphics-
Input := Show[%63,%64]
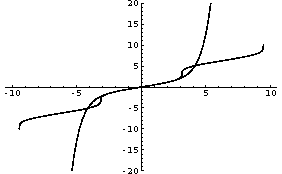
Output = -Graphics-