> alias(u=u(x,t)):

for t >0

> dequ:=exp(t)*diff(u,x)+diff(u,t)=0;

initial condition for u(x,t), x >= 0 (t=0)

> uini:=cos(1/2*pi*x);

The characteristics are now given by

> charequ:=diff(t(x),x)=1/exp(t(x));

This could be solved by separating the variables, but using dsolve is more fun

> chars:=dsolve(charequ,t(x));

> chars2:=subs(_C1=C,rhs(chars));

Let's plot some characteristics

> plot([seq(chars2,C=-5..4)],x=-0.5..4,t=-3.5..1.5);

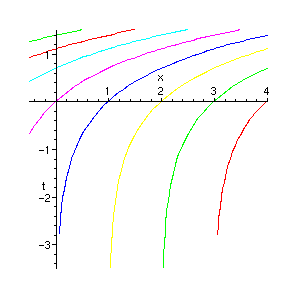
Now, as has been discussed in the text, u(x,t) is constant along these curves. Each curve cuts the x-axis just once and 'picks up' a value of u there, given by the initial condition

> u(x,0)=uini;

> newequ:=t=chars2;

Another vay to write the equations for the characteristic curves

> x=solve(newequ,x);

Hence the function u(x,t) can only have the form

> u(x,t)=F(x-exp(t));

From the initial condition

> F(x-1)=uini;

and by a simple change of variable

> F(x)=subs(x=x+1,uini);

Finally, do the substitution x -> x-ep(t) to get

> F(x-exp(t))=subs(x=x-exp(t)+1,uini);

This is the solution u(x,t) with the given initial condition.