Tehtävä

>

Construction of Green's formula: Llet's find v0 and v1 s.t. Lv0=0, Lv1=0, v0 satisfies the bdary cond at 0, v1 satisfies the boundary condition at 1, and pW=-1, where W is the Wronskian. (From the greenSL.mws)

> restart;

> Grf:=(x,s)->piecewise(s>=0 and s <=x,v1(x)*v0(s),x<=s and s<=1,v0(x)*v1(s));

> with(linalg):

Warning, new definition for norm

Warning, new definition for trace

To obtain the final Green's formula we have to find the solutions v0 and v1 of the homogenous ODE : u''(x)+u(x) = 0. Also v0 and v1 have to satisfy the boundary conditions: v0(0) = 0 and v1(1) = 0. For an equation like u(x) = -u''(x) the first thought for a solution is surely cos(x) or sin(x). Let's take sin(x) because sin(0) = 0.

> v0:=x->a*sin(x);

That's a try for v0, how about v1. We know that v1(1) = 0 so we have to modify v0 a bit to obtain v1.

> v1:=x->b*sin(1-x);

Let's get the Green's formula. ( based on the greenSL.mws)

> Wr:=wronskian([v0(x),v1(x)],x);

> W:=det(Wr);

OOPS!

> pW:=combine(W, trig);

Let's say p = 1 then W = -1 to satisfy the Wronskian. We get for example:

> a:=1; b:=1/sin(1);

> Green:=Grf(x,y);

Finally, let's check the Green's formula we got...

> with(plots):

> plot3d(Green(x,y), x=0..1, y=0..1);

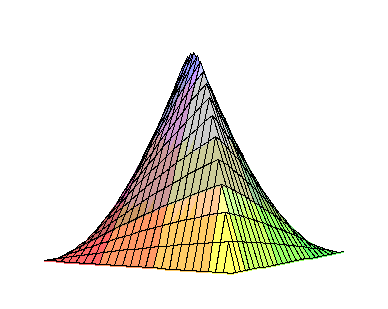
Looks reasonable!