> restart;

Wave Equation

Wave equation for a one dimensional string can be written in the following form:

The solution can obtained by common separation of variables and with the proper initial values like and . For the numerical solving there is one rather a neat method: d'Alembert's formula, which can be used with the initial conditions considered and assuming that x varies over all of R.

Here are some examples of the partial differential equations regarding a string with both ends fixed.

> with(plots):

>

This example considers a string of length L = 20, with fixed endpoints, no initial velocity, and with initial displacement 2 H ( x ), where:

is the triangular pulse function concentrated on the interval [ a , b ] and with peak at p . The solution of the wave equation with these BC's and IC's is:

where the 's are the Fourier sine coefficients of H :

> H:=(n,a,p,b,L)->2*L/((p-a)*(b-p)*n^2*Pi^2)*((b-a)*sin(n*Pi*p/L) -(b-p)*sin(n*Pi*a/L)-(p-a)*sin(n*Pi*b/L));

> ### WARNING: `s` is implicitly declared local
### WARNING: `n` is implicitly declared local
u:=proc(x,t,N) s:=0; for n to N do s:=s+2*H(n,a,p,b,L)*cos(n*Pi*t/L)*sin(n*Pi*x/L) od end;

Warning, `s` is implicitly declared local

Warning, `n` is implicitly declared local

> L:=20;a:=4;p:=5;b:=7;

We will take a = 4, p = 5, b = 7, which means that displacement IC amounts to plucking the subinterval [4,7] at the point 5, giving that point a displacement of 2 (since phi(x) = 2H(x)).
The procedure defining the approximation u(x,t,N) to the solution is:

> animate(u(x,t,51),x=0..20,t=0..20, frames = 21,color=red);

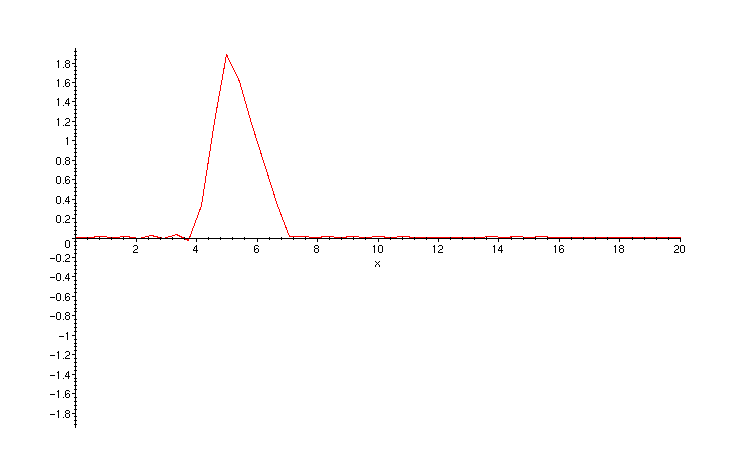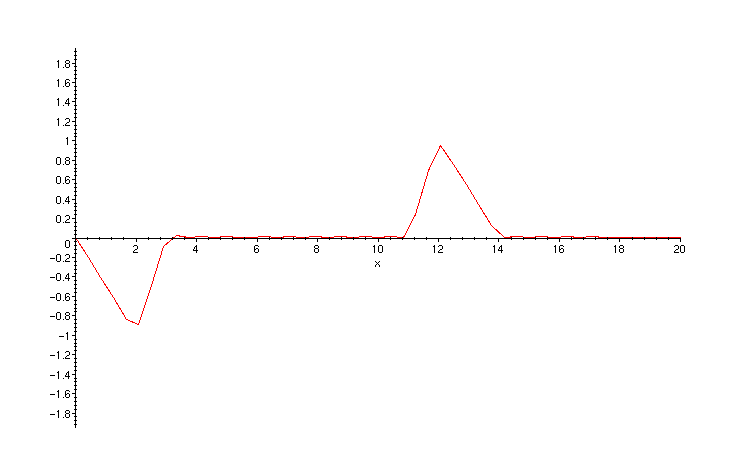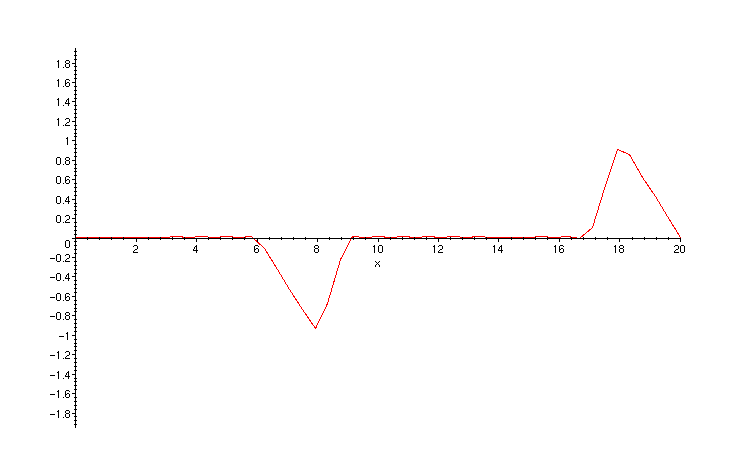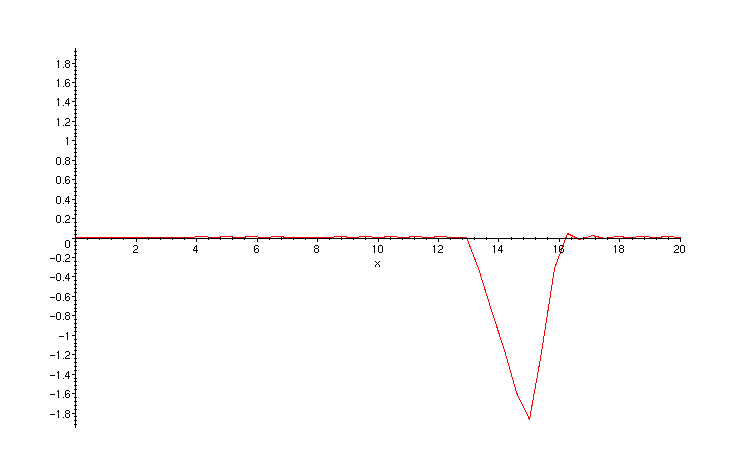
The initial triangular pulse quickly divides into two waves (pulses) of half the amplitude and moving inopposite directions. The left-moving wave reaches the boundary first, is reflected there, and then proceeds to follow the right-moving wave down the string. The orginal right-moving wave reflects at the right boundary and then proceeds to recombine with the original left-moving wave to produce a maximum negative displacement of the string. This occurs at time t = 20 and the shape of the string is precisely the initial shape reflected about the point x = 10 .

The above motion is typical of fixed ends BC's, no initial velocities, and speed c = 1 of propagation. The series solution will be in general:

where the A's are the Fourier sine coefficients of the initial displacement: phi(x). Show that u satisfies the following identities:

or all x and t. Interpret the meaning of these identities in terms of the motion of the string. Generalize this exercise and the above identities to the case when the speed c is arbitrary.

If you run the animation in Exercise (1) backwards, it appears to be a legitimate motion of the string. Show that this is indeed the case by using symmetry, i.e., show that:

satisfies the wave equation, BC's, has the appropriate IC's, and represents the reverse motion of that above, with w(x,L) = .

We next look at the spacetime surface for the motion of the string. This contains all the information (and more) in the animation, but in static form. The figure below is obtained by selecting the appropriate options from the plot menu after executing the following:

> plot3d(u(x,t,51),x=0..20,t=0..25,grid=[50,50]);

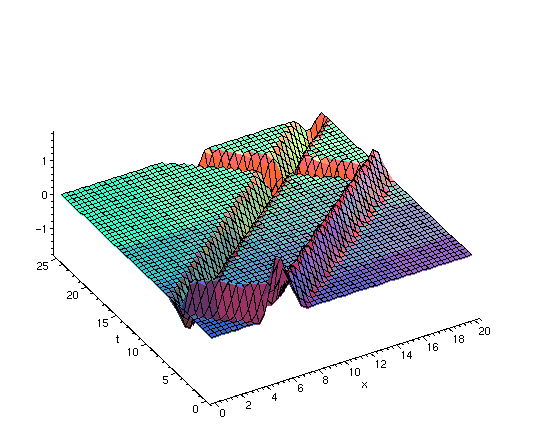
Figure 11.8: Plot of the displacement function u(x,t)
in Example 11.2. The graph of u(x,t) is a surface,
called the spacetime surface for the motion.

The figure clearly shows the initial triangular pulse dividing into left and right moving pulses (of half the magnitude) which propagate down the string, reflect at the boundary, and reunite at time t = L.

>

This Maple worksheet is based on D. Betounes: Partial Differential Equations for Computational Science, Chapter 11, which is available in http://www.math.hut.fi/teaching/osdylask/betounes-koodit/ch11a.mws.

>