25.3.1999
Mikko Kokkonen, 33015p

Solutions to exercises 4

Exercise 1 (Cooper: 9.2/2)

The following plots of the Poisson kernel are produced with a Matlab-script:

a=1, b=0
a=-1/sqrt(2), b=1/sqrt(2)

Exercise 2 (Cooper: 9.2/3)

The following plots of the harmonic functions on the unit disk are produced with another Matlab-script:

r^2 sin(2 theta)
r^7 sin(7 theta)

Exercise 3 (Cooper: 9.2/4)

Since the boundary values are given as a combination of trigonometric functions in polar co-ordinates, the analytic solution is most easily obtained using the Fourier series expansion of the solution (eq. (9.15)). Since f(theta) = 1 + sin(theta), the Fourier coefficients of f are: A_0 = 2, A_n = 0 if n > 0, B_1 = 1, B_n = 0 if n > 1. The solution is obtained by substituting these coefficients into (9.15):

u(r, theta) = 1 + r sin(theta)

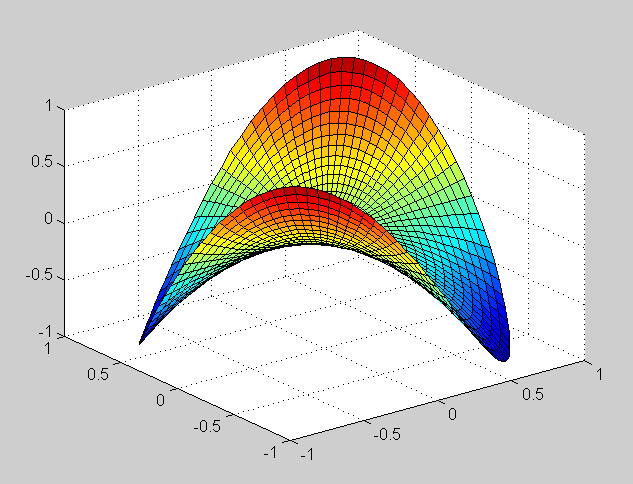
 max u(r, theta) = 1 + max r  max sin(theta) = 2.

The maximum is obtained when r=1, and sin(theta)=1.

 min u(r, theta) >= 1 - r >= 0.

The minimum 0 is obtained when r=1 and sin(theta) = -1.

Verification of the mean value property: we compute the integral of u(r, t) along the circle C_r:

 1 / (2 pi r) int_{C_r} u(r, t) dS,   where dS = r dt
  = 1 / (2 pi r) int_0^{2 pi} (1 + r sin(t)) r dt
  = 1 / (2 pi) [ int_0^{2 pi} dt + r int_0^{2 pi} sin(t) dt ]
  = 1 = u(0, t)

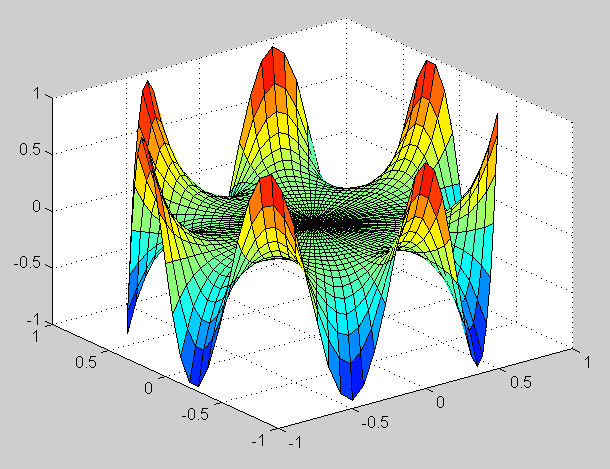
In addition to using the Cooper's matlab-script dirch.m the solution was also computed with numerical integration using the Poisson's kernel. The matlab-code calculates the integral with Simpson's rule and uses the same f.m for boundary values as dirch.m. Surface plots of the solution:

with dirch:
with numerical integration using the Poisson kernel (plot does not include the boundary values):

Exercise 4 (Cooper 9.2/5)

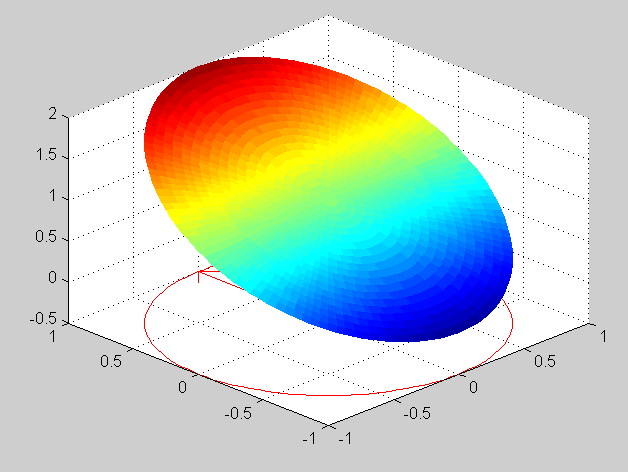
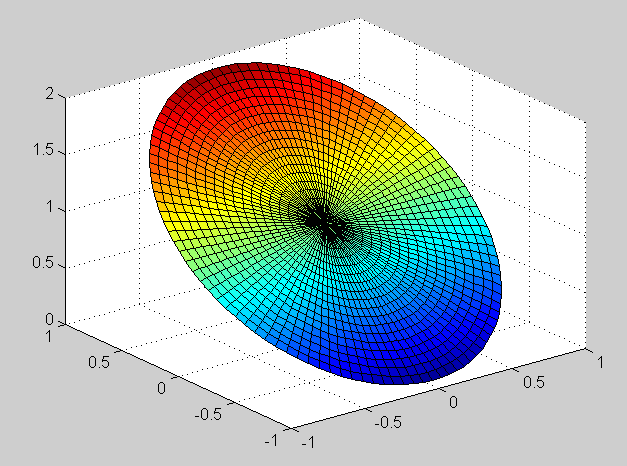
f(t) = 2 + sin(t) / 2 - cos(t) / 10 + sin^2 (t) + cos (4t)
     = 2 + sin(t) / 2 - cos(t) / 10 + 1/2 - cos(2t) / 2 + cos(4t)
     = 5/2 + sin(t) / 2 - cos(t) / 10 - cos(2t) / 2 + cos(4t)

The Fourier coefficients of f are: A_0 = 5, A_1 = -1/10, A_2 = - 1/2, A_3 = 0, A_4 = 1, A_n = 0 if n > 4, B_1 = 1/2, B_n = 0 if n > 1. The solution is

 u(r, theta) = 5/2 + r (sin(theta) / 2 - cos(theta) / 10) - r^2 cos(2
theta) / 2 + r^4 cos(4 theta)

The verification of the mean value property goes in the same way as in the previous exercise. We can note that integrals of sin(n t) and cos(n t) from 0 to 2 pi are zero, because the integral function is 2 pi -periodic.

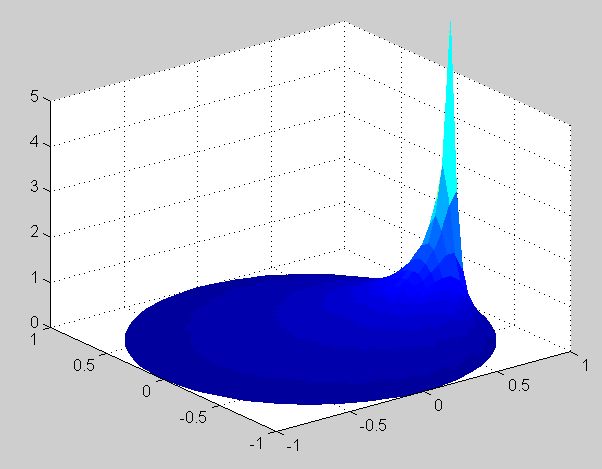
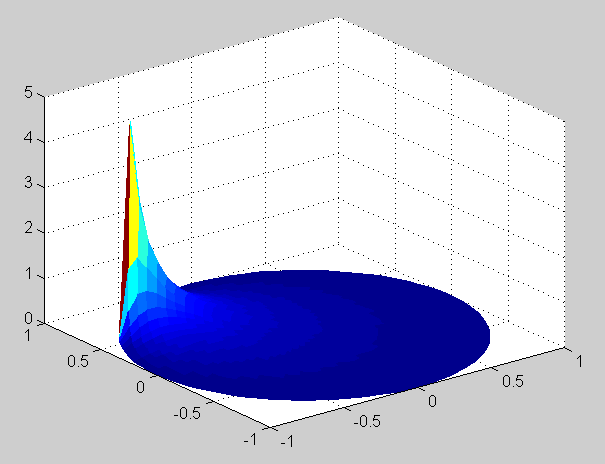
Maximum value (from the numerical solution) is 4.5 and minimum is 1.0603, their location is on the boundary as can be seen in the surface plots of the solution:

with dirch:
with numerical integration using the Poisson kernel:

Exercise NN (Cooper: 9.2/6)

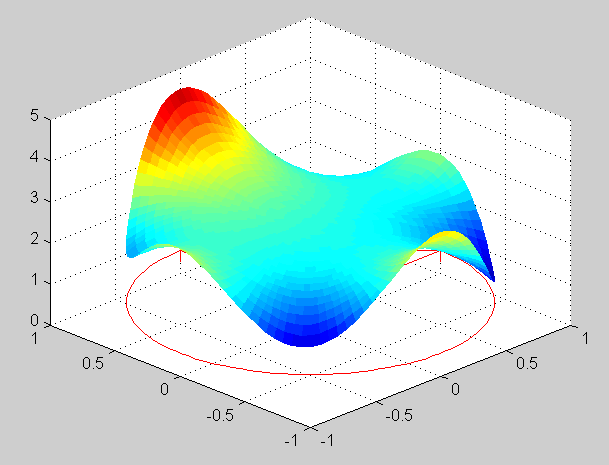
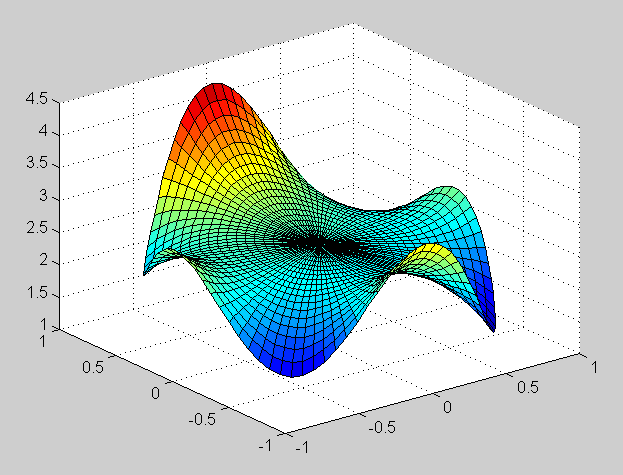
f(t) = cos(t) + 4 sin^3(t)
     = cos(t) + 4 sin(t) [1 - cos^2(t)]
     = cos(t) + 4 sin(t) + 2 sin(t) [cos(2t) - 1]
     = cos(t) + 2 sin(t) + sin(3t) - sin(t)
     = cos(t) + sin(t) + sin(3t).

The Fourier coefficients of f are: A_0 = 0, A_1 = 1, A_n = 0 if n>1, B_1 = 1, B_2 = 0, B_3 = 1, B_n = 0 if n>3. The solution is:

 u(r, theta) = r [cos(theta) + sin(theta)] + r^3 sin(3 theta)

Verification of the mean value property is done in the same way as in previous exercises. The maximum of the solution is 4.0405 and the minimum is -4.0405. Surface plots of the solution:

with dirch:
with numerical integration using the Poisson kernel:

Exercise 5 (Cooper: 9.2/7)

The maximum of the solution is 0.9819 and the minimum is -2.9153. Surface plots of the solution:

with dirch:
with numerical integration using the Poisson kernel:

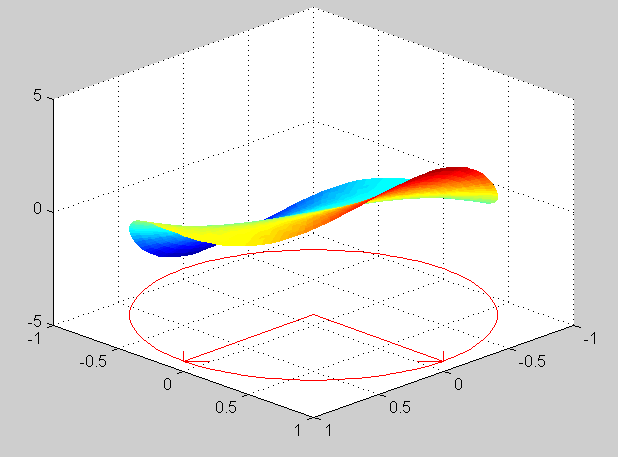
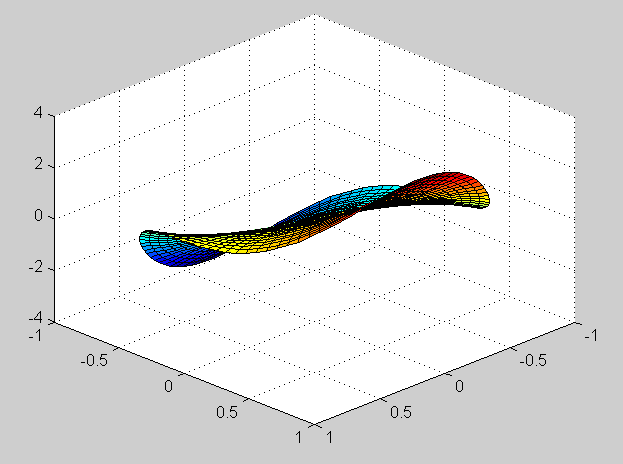
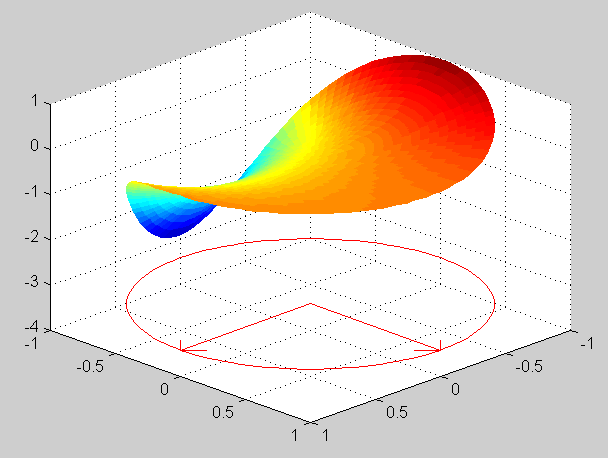
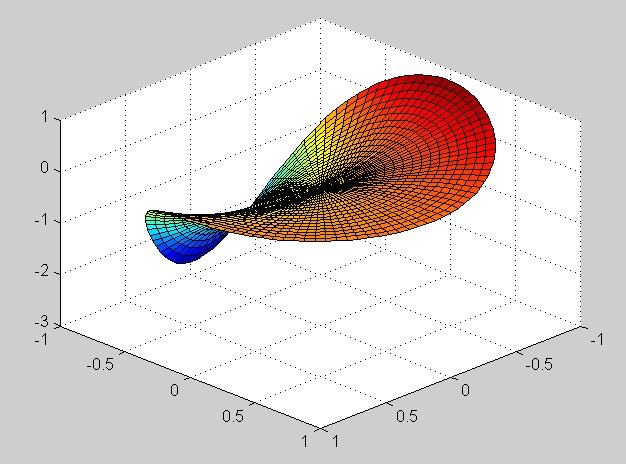
u(0,0) = int_0^2 pi f(theta) d theta
       = erf(pi) / (2 sqrt(pi)) - 3 [erf(pi / sqrt(2)) + erf(3 pi/sqrt(2))] /
                                            (4 sqrt(pi))
       approx -0.3179

Value of the solution provided by dirch.m at (0, 0) is -0.3157

Exercise 6 (Cooper: 9.2/8)

Equating the coefficients of sin(n theta) and cos(n theta) in the Fourier expansions of g(theta) and d u(r, theta) / dr we obtain the conditions:

n rho^{n-1} a_n = A_n   and   n rho^{n-1} b_n = B_n

so that

a_n = A_n / ( n rho^{n-1} )  and  b_n = B_n / ( n rho^{n-1} )

The compatibility condition for g(theta) is obtained e.g. from TW Lemma 7.1, which says that if u is harmonic, then du / dn integrated along the boundary is zero. For g(theta) this means that int_pi^pi g(theta) dtheta = 0. If the series expansion for g(theta) converges uniformly, we may integrate term by term and obtain a condition that A_0 = 0.

Since the boundary conditions are for the first derivative of u, the solution is unique up to a constant value.

Exercise 7

Solution shown within previous solutions.