First some general definitions from the GreenSL.mws worksheet:

> Grf:=(x,s)->piecewise(s>=0 and s <=x,v1(x)*v0(s),x<=s and s<=1,v0(x)*v1(s));

> with(linalg):

Next we need to find solutions v0 and v1 to the homogenous equation u''(x) + u(x) = 0, such that v0 satisfies the boundary condition on the left v0(0)=0 and v1 satisfies the boundary o condition on the right v1(1) = 0. Also p det W=-1, here p=1. We claim that these are:

> v0:=x->a*sin(x);

> v1:=x->b*sin(1-x);

Verification of the ODE:

> diff(v1(x), x$2) + v1(x); diff(v0(x), x$2)+v0(x);

Verification of the boundary conditions:

> v0(0); v1(1);

The Wronskian:

> W:=wronskian([v0(x),v1(x)],x);

> W:=combine(expand(det(W)), trig);

The condition for the wronskian is satisfied if we choose:

> a:=1; b:=1/sin(1);

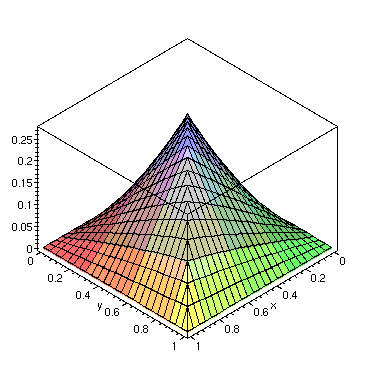
Now the Green's function for this problem is:

> G:=Grf(x,y);

> with(plots):

> plot3d(G(x,y),x=0..1,y=0..1,axes=boxed);

>